Différences finies (méthode des) (HU) : Différence entre versions
(discuter) |
|||
| Ligne 1 : | Ligne 1 : | ||
''<u>Traduction anglaise</u> : Finite differences method'' | ''<u>Traduction anglaise</u> : Finite differences method'' | ||
| − | Méthode numérique de résolution des équations | + | Méthode numérique de résolution des équations différentielles ou des équations aux dérivées partielles. |
| − | différentielles ou des équations aux dérivées partielles | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ==Principe de la méthode== | ||
| + | Cette méthode consiste à remplacer les opérateurs différentiels par des opérateurs algébriques qui constituent des approximations numériques de leurs valeurs en un point. A titre d'exemple, l'opérateur différentiel : dy / dx, peut être remplacé par la quantité : Δy / Δx où Δx possède une longueur finie ([[Discrétisation (HU)|Discrétisation]] du domaine). Géométriquement, dans le cas d'une différence centrée à deux pas, cette transformation particulière revient à remplacer la pente de la droite tangente au graphe de la fonction y = f(x), au point x, par la pente de la droite joignant les points [x-Δx, f(x-Δx)], [x+Δx, f(x+Δx)]. | ||
| − | |||
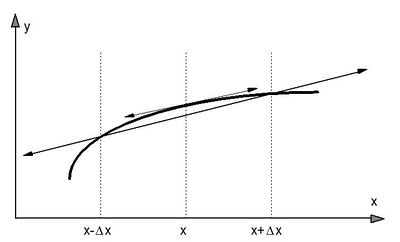
| + | [[File:differences finies.JPG|400px|center|thumb|<center>''Représentation graphique de l’opérateur algébrique équivalent à l’opérateur dérivée première : exemple d’un schéma centré à deux pas.''</center>]] | ||
| + | Au lieu de chercher la solution sous la forme d'une fonction continue, y = f(x), on se contente de rechercher une table de valeurs numériques y<sub>i</sub>, approchant les valeurs exactes de la fonction f(x) sur un réseau prédéfini de nœuds de calcul. | ||
| − | + | ==Application en hydrologie== | |
| − | + | ||
| − | + | ||
| − | + | Cette méthode possède de nombreuses applications en hydrologie urbaine. Citons en particulier la résolution numérique des équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]], la méthode [Muskingum (Modèle) (HU)|Muskingum]], l'intégration de la ligne d'eau, etc. Elle donne généralement de bons résultats mais impose des contraintes sur le choix du pas de temps et du (ou des) pas d'espace pour assurer la stabilité des résultats. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Cette méthode possède de nombreuses applications en hydrologie urbaine. Citons | + | |
| − | en particulier la résolution numérique des équations de [[Barré de Saint Venant (équations de) (HU)|Barré de Saint Venant]], la méthode | + | |
| − | + | ||
| − | l'intégration de la ligne d'eau, etc. Elle donne généralement de bons résultats | + | |
| − | mais impose des contraintes sur le choix du pas de temps et du (ou des) pas d'espace | + | |
| − | pour assurer la stabilité des résultats. | + | |
| − | [[Catégorie: | + | [[Catégorie:Outils_mathématiques_(HU)]] |
Version du 4 avril 2020 à 16:17
Traduction anglaise : Finite differences method
Méthode numérique de résolution des équations différentielles ou des équations aux dérivées partielles.
Principe de la méthode
Cette méthode consiste à remplacer les opérateurs différentiels par des opérateurs algébriques qui constituent des approximations numériques de leurs valeurs en un point. A titre d'exemple, l'opérateur différentiel : dy / dx, peut être remplacé par la quantité : Δy / Δx où Δx possède une longueur finie (Discrétisation du domaine). Géométriquement, dans le cas d'une différence centrée à deux pas, cette transformation particulière revient à remplacer la pente de la droite tangente au graphe de la fonction y = f(x), au point x, par la pente de la droite joignant les points [x-Δx, f(x-Δx)], [x+Δx, f(x+Δx)].
Au lieu de chercher la solution sous la forme d'une fonction continue, y = f(x), on se contente de rechercher une table de valeurs numériques yi, approchant les valeurs exactes de la fonction f(x) sur un réseau prédéfini de nœuds de calcul.
Application en hydrologie
Cette méthode possède de nombreuses applications en hydrologie urbaine. Citons en particulier la résolution numérique des équations de Barré de Saint Venant, la méthode [Muskingum (Modèle) (HU)|Muskingum]], l'intégration de la ligne d'eau, etc. Elle donne généralement de bons résultats mais impose des contraintes sur le choix du pas de temps et du (ou des) pas d'espace pour assurer la stabilité des résultats.
 S'abonner à un flux RSS
S'abonner à un flux RSS