Jean-Michel Tanguy/SujetENTPE2022/BEAUDET - MIGEON - MOBISSON : Différence entre versions
(→Modèle de Berkhoff) |
|||
| Ligne 54 : | Ligne 54 : | ||
[[File:cylindre.png|400pxvignette|Phénomène de réfraction de la houle]] | [[File:cylindre.png|400pxvignette|Phénomène de réfraction de la houle]] | ||
<br /> | <br /> | ||
| − | La condition de Dirichlet : <math> \phi </math> = 1 à l'entrée du canal | + | La condition de Dirichlet : <math> \displaystyle \phi </math> = 1 à l'entrée du canal |
| − | La condition de Robin : <math> \phi_{x} = ik\phi </math> à la sortie du canal | + | La condition de Robin : <math> \displaystyle \phi_{x} = ik\phi </math> à la sortie du canal |
Pour simplifier la résolution on suppose que ces conditions sont imposées en x = 0 | Pour simplifier la résolution on suppose que ces conditions sont imposées en x = 0 | ||
| Ligne 68 : | Ligne 68 : | ||
On a l'équation : <math> \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 </math> | On a l'équation : <math> \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 </math> | ||
| − | L'équation caractéristique associée s'écrit : <math> x^2+k^2 = 0 </math> | + | L'équation caractéristique associée s'écrit : <math> \displaystyle x^2+k^2 = 0 </math> |
| − | Le déterminant de cette équation vaut : <math> \Delta = -4k^2 < 0 </math> | + | Le déterminant de cette équation vaut : <math> \displaystyle \Delta = -4k^2 < 0 </math> |
| − | La solution est donc complexe et s'écrit sous la forme : <math> \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} </math> | + | La solution est donc complexe et s'écrit sous la forme : <math> \displaystyle \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} </math> |
On peut déterminer les constantes A et B à l'aide des conditions aux limites: | On peut déterminer les constantes A et B à l'aide des conditions aux limites: | ||
| − | - <math> \phi(x=0) = A+B = 1 </math> | + | - <math> \displaystyle \phi(x=0) = A+B = 1 </math> |
| − | - <math> \dfrac{\partial \phi}{\partial x}(x=l) = ik\phi </math> | + | - <math> \displaystyle \dfrac{\partial \phi}{\partial x}(x=l) = ik\phi </math> |
| − | On en déduit: <math> A = 0 ; B = 1 </math> | + | On en déduit: <math> \displaystyle A = 0 ; B = 1 </math> |
| − | On a alors : <math> \phi(x,t) = \mathrm{e}^{(i(kx-\omega t))} </math> | + | On a alors : <math> \displaystyle \phi(x,t) = \mathrm{e}^{(i(kx-\omega t))} </math> |
L'évolution de la hauteur de la houle s'écrit donc : | L'évolution de la hauteur de la houle s'écrit donc : | ||
| − | <math> h(x,t) = Re(\phi(x,t)) = cos(kx-\omega t) </math> | + | <math> \displaystyle h(x,t) = Re(\phi(x,t)) = cos(kx-\omega t) </math> |
=== Solution par méthode d'homotopie === | === Solution par méthode d'homotopie === | ||
| Ligne 104 : | Ligne 104 : | ||
On a donc p = 0 et <math> \displaystyle \phi_{0,xx}=0 </math> | On a donc p = 0 et <math> \displaystyle \phi_{0,xx}=0 </math> | ||
| − | On obtient la relation suivante : <math> \phi_0=Ax+B </math> | + | On obtient la relation suivante : <math> \displaystyle \phi_0=Ax+B </math> |
Avec les conditions initiales on a : | Avec les conditions initiales on a : | ||
| − | <math> \phi_{0}(x=0)=1 </math> et donc <math> | + | <math> \displaystyle \phi_{0}(x=0)=1 </math> et donc <math> \displaystyle B = 1 </math> |
| − | <math> \Leftrightarrow \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_{0}(x=L) </math> | + | <math> \displaystyle \Leftrightarrow \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_{0}(x=L) </math> |
| − | <math> \Leftrightarrow A=ik(AL+1) </math> | + | <math> \displaystyle \Leftrightarrow A=ik(AL+1) </math> |
| − | <math> \Leftrightarrow A=\frac{ik}{1-ikL} </math> | + | <math> \displaystyle \Leftrightarrow A=\frac{ik}{1-ikL} </math> |
| − | donc <math> \phi_0=\frac{ik}{1-ikL}x+1 </math> | + | donc <math> \displaystyle \phi_0=\frac{ik}{1-ikL}x+1 </math> |
* <big>Ordre 1</big> | * <big>Ordre 1</big> | ||
On a p = 1 et la relation : <math> \displaystyle \phi_{1,xx}=0 </math> | On a p = 1 et la relation : <math> \displaystyle \phi_{1,xx}=0 </math> | ||
| − | <math> \Leftrightarrow \phi_1= -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2})+Cx+D </math> | + | <math> \displaystyle \Leftrightarrow \phi_1= -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2})+Cx+D </math> |
A l'aide des conditions aux limites : | A l'aide des conditions aux limites : | ||
| − | - <math> \phi_1(x=0) = 0 </math> | + | - <math> \displaystyle \phi_1(x=0) = 0 </math> |
| − | - <math> \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_1(x=L) </math> | + | - <math> \displaystyle \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_1(x=L) </math> |
On obtient: | On obtient: | ||
| − | <math> ik(-k^2(\frac{ikL^3}{6(1-ikL)}+\frac{L^2}{2})+CL) =-k^2(\frac{ikL^2}{2(1-ikL)}+L)+C </math> | + | <math> \displaystyle ik(-k^2(\frac{ikL^3}{6(1-ikL)}+\frac{L^2}{2})+CL) =-k^2(\frac{ikL^2}{2(1-ikL)}+L)+C </math> |
| − | <math> \Leftrightarrow C = -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2} </math> | + | <math> \displaystyle \Leftrightarrow C = -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2} </math> |
| − | On a alors : <math> \phi_1 = -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2}) -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2}x </math> | + | On a alors : <math> \displaystyle \phi_1 = -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2}) -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2}x </math> |
* Ordres 2 et supérieurs | * Ordres 2 et supérieurs | ||
| Ligne 137 : | Ligne 137 : | ||
Afin de les déterminer, on s'aidera des relations : | Afin de les déterminer, on s'aidera des relations : | ||
| − | - Longueur : <math> L = 2\lambda </math> (m) | + | - Longueur : <math> \displaystyle L = 2\lambda </math> (m) |
| − | - Profondeur : <math> H = 40 </math> (m) | + | - Profondeur : <math> \displaystyle H = 40 </math> (m) |
| − | - Longueur d'onde : <math> \lambda = \frac{2\pi}{k} </math> (m) | + | - Longueur d'onde : <math> \displaystyle \lambda = \frac{2\pi}{k} </math> (m) |
| − | - Nombre d'onde : <math> k = \frac{1}{100} </math> | + | - Nombre d'onde : <math> \displaystyle k = \frac{1}{100} </math> |
| − | - Vitesse de l'onde : <math> c = \sqrt{gH} </math> (m/s) | + | - Vitesse de l'onde : <math> \displaystyle c = \sqrt{gH} </math> (m/s) |
== Deuxième Cas == | == Deuxième Cas == | ||
Ce deuxième correspond de même à un canal de longueur L. Néanmoins, nous avons désormais les conditions aux limites : | Ce deuxième correspond de même à un canal de longueur L. Néanmoins, nous avons désormais les conditions aux limites : | ||
| − | - flux en aval : <math> \phi_x(x=0) = ik(2-\phi(x=0)) </math> | + | - flux en aval : <math> \displaystyle \phi_x(x=0) = ik(2-\phi(x=0)) </math> |
| − | - réflexion totale en amont : <math> \phi_x(x=L) = 0 </math> | + | - réflexion totale en amont : <math> \displaystyle \phi_x(x=L) = 0 </math> |
=== Solution analytique === | === Solution analytique === | ||
On a l'équation : <math> \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 </math> | On a l'équation : <math> \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 </math> | ||
| − | L'équation caractéristique associée s'écrit : <math> x^2+k^2 = 0 </math> | + | L'équation caractéristique associée s'écrit : <math> \displaystyle x^2+k^2 = 0 </math> |
| − | Le déterminant de cette équation vaut : <math> \Delta = -4k^2 < 0 </math> | + | Le déterminant de cette équation vaut : <math> \displaystyle \Delta = -4k^2 < 0 </math> |
| − | La solution est donc complexe et s'écrit sous la forme : <math> \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} </math> | + | La solution est donc complexe et s'écrit sous la forme : <math> \displaystyle \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} </math> |
On peut déterminer les constantes A et B à l'aide des conditions aux limites: | On peut déterminer les constantes A et B à l'aide des conditions aux limites: | ||
| − | - <math> \dfrac{\partial \phi}{\partial x}(x=0) = ik(2-\phi(x=0) \Leftrightarrow -ikA+ikB = ik(2-A-B) \Leftrightarrow B = 1 </math> | + | - <math> \displaystyle \dfrac{\partial \phi}{\partial x}(x=0) = ik(2-\phi(x=0) \Leftrightarrow -ikA+ikB = ik(2-A-B) \Leftrightarrow B = 1 </math> |
| − | - <math> \dfrac{\partial \phi}{\partial x}(x=l) = 0 \Leftrightarrow --ikA\mathrm{e}^{(-ikL)}+ikB\mathrm{e}^{(ikL)} = 0 \Leftrightarrow A = \mathrm{e}^{(2ikL)} </math> | + | - <math> \displaystyle \dfrac{\partial \phi}{\partial x}(x=l) = 0 \Leftrightarrow --ikA\mathrm{e}^{(-ikL)}+ikB\mathrm{e}^{(ikL)} = 0 \Leftrightarrow A = \mathrm{e}^{(2ikL)} </math> |
On a donc : | On a donc : | ||
| − | <math> h(x,t) = Re(\phi(x,t)) = cos(k(2L-x) - \omega t) </math> | + | <math> \displaystyle h(x,t) = Re(\phi(x,t)) = cos(k(2L-x) - \omega t) </math> |
=== Solution par méthode d'homotopie === | === Solution par méthode d'homotopie === | ||
| − | On procède de la même manière que pour la cas 1 en trouvant <math> /phi </math> aux différents ordres. | + | On procède de la même manière que pour la cas 1 en trouvant <math> \displaystyle /phi </math> \displaystyle aux différents ordres. |
* Ordre 0 | * Ordre 0 | ||
| Ligne 180 : | Ligne 180 : | ||
On a alors la relation : <math> \phi_{0,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2} = 0 </math> | On a alors la relation : <math> \phi_{0,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2} = 0 </math> | ||
| − | <math> \Leftrightarrow \phi = Ax+B </math> | + | <math> \displaystyle \Leftrightarrow \phi = Ax+B </math> |
A l'aide des conditions aux limites: | A l'aide des conditions aux limites: | ||
| − | - <math> \dfrac{\partial \phi_0}{\partial x}(x=0) = ik(2-\phi_0(x=0)) \Leftrightarrow ik(2-B) = 0 \Leftrightarrow B = 2 </math> | + | - <math> \displaystyle \dfrac{\partial \phi_0}{\partial x}(x=0) = ik(2-\phi_0(x=0)) \Leftrightarrow ik(2-B) = 0 \Leftrightarrow B = 2 </math> |
| − | - <math> \dfrac{\partial \phi_0}{\partial x}(x=L) = 0 \Leftrightarrow A = 0 </math> | + | - <math> \displaystyle \dfrac{\partial \phi_0}{\partial x}(x=L) = 0 \Leftrightarrow A = 0 </math> |
On a donc <math> \phi_0 = 2 </math> | On a donc <math> \phi_0 = 2 </math> | ||
| Ligne 192 : | Ligne 192 : | ||
On a pour ce cas p = 1 | On a pour ce cas p = 1 | ||
On a alors la relation : | On a alors la relation : | ||
| − | <math> \phi_{1,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2}+k^2\phi_0 = 0 \Leftrightarrow \phi_1 = -k^2x^2+Cx+D </math> | + | <math> \displaystyle \phi_{1,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2}+k^2\phi_0 = 0 \Leftrightarrow \phi_1 = -k^2x^2+Cx+D </math> |
A l'aide des conditions aux limites : | A l'aide des conditions aux limites : | ||
| − | - <math> \dfrac{\partial \phi_1}{\partial x}(x=0) = ik\phi_1(x=0) \Leftrightarrow ikD = 2k^2L \Leftrightarrow D = 2ikL </math> | + | - <math> \displaystyle \dfrac{\partial \phi_1}{\partial x}(x=0) = ik\phi_1(x=0) \Leftrightarrow ikD = 2k^2L \Leftrightarrow D = 2ikL </math> |
| − | - <math> \dfrac{\partial \phi_1}{\partial x}(x=L) = 0 \Leftrightarrow C = 2k^2L </math> | + | - <math> \displaystyle \dfrac{\partial \phi_1}{\partial x}(x=L) = 0 \Leftrightarrow C = 2k^2L </math> |
| − | On a donc <math> \phi_1 = -k^2x^2+2k^2Lx+2ikL </math> | + | On a donc <math> \displaystyle \phi_1 = -k^2x^2+2k^2Lx+2ikL </math> |
== Troisième Cas == | == Troisième Cas == | ||
| Ligne 209 : | Ligne 209 : | ||
- k non constant : <math> \displaystyle k(x) = k_0\sqrt{\dfrac{H_0}{H(x)}} = k_0\sqrt{\dfrac{H_0}{H_0 - sx}} </math> | - k non constant : <math> \displaystyle k(x) = k_0\sqrt{\dfrac{H_0}{H(x)}} = k_0\sqrt{\dfrac{H_0}{H_0 - sx}} </math> | ||
| − | - <math> CC_g = gH(x) </math> | + | - <math> \displaystyle CC_g = gH(x) </math> |
On obtient alors pour l'équation de Berkhoff : | On obtient alors pour l'équation de Berkhoff : | ||
| Ligne 229 : | Ligne 229 : | ||
on a ainsi les conditions suivantes : | on a ainsi les conditions suivantes : | ||
| − | - <math> \phi_rr + \frac{1}{r}\phi_r + k^2\phi = 0 </math> (symétrie de révolution, donc indépendant de <math> \theta </math> ) | + | - <math> \displaystyle \phi_rr + \frac{1}{r}\phi_r + k^2\phi = 0 </math> (symétrie de révolution, donc indépendant de <math> \theta </math> ) |
| − | - <math> \phi(r=r_0) = 1 </math> | + | - <math> \displaystyle \phi(r=r_0) = 1 </math> |
| − | - <math> \phi_r(r=R) = ik \phi(r=R) </math> | + | - <math> \displaystyle \phi_r(r=R) = ik \phi(r=R) </math> |
| Ligne 244 : | Ligne 244 : | ||
* Ordre 0 | * Ordre 0 | ||
On a pour ce cas p = 0 | On a pour ce cas p = 0 | ||
| − | On a la relation : <math> \phi_0,rr = 0 \Leftrightarrow \phi_0 = Ar+B </math> | + | On a la relation : <math> \displaystyle \phi_0,rr = 0 \Leftrightarrow \phi_0 = Ar+B </math> |
A l'aide des conditions aux limites : | A l'aide des conditions aux limites : | ||
| − | - <math> \phi_0(r=r_0) = 1 \Leftrightarrow Ar_0+B = 1 </math> | + | - <math> \displaystyle \phi_0(r=r_0) = 1 \Leftrightarrow Ar_0+B = 1 </math> |
| − | - <math> \phi_r(r=R) = ik \phi(r=R) \Leftrightarrow A = ik(AR+B) </math> | + | - <math> \displaystyle \phi_r(r=R) = ik \phi(r=R) \Leftrightarrow A = ik(AR+B) </math> |
| − | On a donc : <math> A = \frac{ik}{1+ik(r_0-R)} </math> et <math> B = \frac{1-ikR}{1+ik(r_0-R)} </math> | + | On a donc : <math> \displaystyle A = \frac{ik}{1+ik(r_0-R)} </math> et <math> B = \frac{1-ikR}{1+ik(r_0-R)} </math> |
On en déduit alors : | On en déduit alors : | ||
| − | <math> \phi_0 = \frac{ik}{1+ik(r_0-R)} r + \frac{1-ikR}{1+ik(r_0-R)} </math> | + | <math> \displaystyle \phi_0 = \frac{ik}{1+ik(r_0-R)} r + \frac{1-ikR}{1+ik(r_0-R)} </math> |
* Ordre 1 | * Ordre 1 | ||
On a pour ce cas p = 1 | On a pour ce cas p = 1 | ||
Version du 24 mai 2022 à 16:39
Sommaire |
Introduction
Contexte
Aujourd'hui, le changement climatique et l'augmentation de la température constituent des enjeux majeurs pour la planète, et plus spécialement pour les populations vivant le long des côtes avec une importante hausse du niveau des océans Les deux principales causes de ce haussement sont la fonte des glaciers continentaux et la dilatation thermique des océans. Selon l'U.S Global Change Reserach Program for the Fourth National Climate Assessment, entre 1900 et 2018, le niveau moyen des océans s'est élevé d'environ 20 cm, et cela s'accélère à partie de 2020 allant jusqu'à plus de 3,5 mm par an. De nombreux scientifiques estiment que le niveau de la mer pourrait avoir augmenté de 1 à 3 mètres d'ici 2100. Une telle hausse du niveau de la mer pourrait entraîner la suppression de terres ainsi que le déplacement de populations côtières.
La houle correspond au mouvements de la mer de façon ondulatoire, provoqués des zones de vents lointaines. L'étude suivante a pour but d'étudier son impact sur les littoraux, entraînant de plus en plus de conséquences extrêmes. Ces études utilisent des modélisations numériques représentant la houle, tel que le modèle de Berkhoff constitué d'Equations aux Dérivées Partielles, en prenant en compte une représentation des phénomènes de shoaling, réfraction, diffraction et réflexion des différentes structures le long des côtes.
Phénomène de Houle
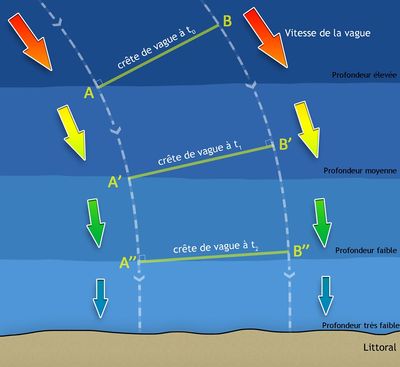
Lorsque la houle se rapproche des côtes la topographie sous-marine modifie la houle à travers différents phénomènes.
Réfraction : C'est le phénomène majeur qui a lieu. Plus la houle se rapproche de la côte et donc plus la profondeur diminue plus les lignes de crêtes vont être parallèles au rivage.
Diffraction : phénomène lorsque la houle rencontre un obstacle plus petit ou une ouverture.
Réflexion : Ce phénomène a lieu lorsque la houle rencontre une structure profonde et large par rapport à la longueur d'onde de cette dernière.
Shoaling : Effet des vagues de surfaces entrant dans des eaux moins profondes modifiant ainsi la profondeur des vagues.
Modèle de Berkhoff
Le modèle de Berkhoff permet de représenter les phénomènes de réfraction, diffraction et de réflexion que subit la houle. Cette équation a été introduite par Berkhoff en 1973 sous la forme :
$ \displaystyle \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $
Avec :
$ \displaystyle \phi $ : le potentiel
k : le nombre d’onde fonction de H (profondeur) et de ω (fréquence) avec $ \omega^2=gk \tanh(kH) $
C : la célérité de l'onde
Cg : célérité de groupe de vagues
- Les hypothèses pour ce modèle :
Nous nous placerons pour la suite dans un modèle linéaire et donc nous approximerons :
- $ \displaystyle C = Cg = \sqrt{gH} $
- $ \displaystyle h(x,t) = \mathrm{R}\phi e^{-i\omega t} $ qui correspond à l'évolution dans le temps et la distance de la houle
Homotopie
Premier Cas
Nous nous plaçons dans le cas d'un canal unidimensionnel de longueur L avec 2 conditions limites.

La condition de Dirichlet : $ \displaystyle \phi $ = 1 à l'entrée du canal
La condition de Robin : $ \displaystyle \phi_{x} = ik\phi $ à la sortie du canal
Pour simplifier la résolution on suppose que ces conditions sont imposées en x = 0
On peut alors simplifier l'écriture de l'équation de Berkhoff tel que :
- $ \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $
Solution analytique
On a l'équation : $ \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $
L'équation caractéristique associée s'écrit : $ \displaystyle x^2+k^2 = 0 $
Le déterminant de cette équation vaut : $ \displaystyle \Delta = -4k^2 < 0 $
La solution est donc complexe et s'écrit sous la forme : $ \displaystyle \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} $
On peut déterminer les constantes A et B à l'aide des conditions aux limites:
- $ \displaystyle \phi(x=0) = A+B = 1 $
- $ \displaystyle \dfrac{\partial \phi}{\partial x}(x=l) = ik\phi $
On en déduit: $ \displaystyle A = 0 ; B = 1 $
On a alors : $ \displaystyle \phi(x,t) = \mathrm{e}^{(i(kx-\omega t))} $
L'évolution de la hauteur de la houle s'écrit donc : $ \displaystyle h(x,t) = Re(\phi(x,t)) = cos(kx-\omega t) $
Solution par méthode d'homotopie
On obtient la relation par homotopie à l'aide :
- de la dérivée seconde qui correspond à l'opérateur linéaire
- d'une solution initiale nulle $ \displaystyle (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $
On remplace ensuite dans la solution initiale nulle la décomposition en série entière (en rouge) et la dérivée de cette dernière (en vert) :
$ \displaystyle (1-p)({\color{Green}\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...})+p[{\color{Green}\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)}+...+k^2({\color{Red}\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...})]=0 $
Il faut ensuite simplifier et écrire cette relation suivant les puissances de p croissantes. Cette relation étant valable quel que soit p, tous les coefficients devant les puissances de p sont donc nuls. ??
- Ordre 0
On a donc p = 0 et $ \displaystyle \phi_{0,xx}=0 $
On obtient la relation suivante : $ \displaystyle \phi_0=Ax+B $ Avec les conditions initiales on a :
$ \displaystyle \phi_{0}(x=0)=1 $ et donc $ \displaystyle B = 1 $
$ \displaystyle \Leftrightarrow \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_{0}(x=L) $
$ \displaystyle \Leftrightarrow A=ik(AL+1) $
$ \displaystyle \Leftrightarrow A=\frac{ik}{1-ikL} $
donc $ \displaystyle \phi_0=\frac{ik}{1-ikL}x+1 $
- Ordre 1
On a p = 1 et la relation : $ \displaystyle \phi_{1,xx}=0 $ $ \displaystyle \Leftrightarrow \phi_1= -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2})+Cx+D $
A l'aide des conditions aux limites :
- $ \displaystyle \phi_1(x=0) = 0 $
- $ \displaystyle \dfrac{\partial \phi_{0}}{\partial x}(x=L)=ik \phi_1(x=L) $
On obtient: $ \displaystyle ik(-k^2(\frac{ikL^3}{6(1-ikL)}+\frac{L^2}{2})+CL) =-k^2(\frac{ikL^2}{2(1-ikL)}+L)+C $ $ \displaystyle \Leftrightarrow C = -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2} $
On a alors : $ \displaystyle \phi_1 = -k^2(\frac{ikx^3}{6(1-ikL)}+\frac{x^2}{2}) -\frac{k^2L(k^2L^2+3ikl-3)}{3(1-ikl)^2}x $
- Ordres 2 et supérieurs
En vue des calculs de plus en plus complexes à réaliser, on utilise le logiciel WSMAXIMA dans le but de trouver $ \phi $ à ces ordres. Afin de les déterminer, on s'aidera des relations :
- Longueur : $ \displaystyle L = 2\lambda $ (m)
- Profondeur : $ \displaystyle H = 40 $ (m)
- Longueur d'onde : $ \displaystyle \lambda = \frac{2\pi}{k} $ (m)
- Nombre d'onde : $ \displaystyle k = \frac{1}{100} $
- Vitesse de l'onde : $ \displaystyle c = \sqrt{gH} $ (m/s)
Deuxième Cas
Ce deuxième correspond de même à un canal de longueur L. Néanmoins, nous avons désormais les conditions aux limites :
- flux en aval : $ \displaystyle \phi_x(x=0) = ik(2-\phi(x=0)) $
- réflexion totale en amont : $ \displaystyle \phi_x(x=L) = 0 $
Solution analytique
On a l'équation : $ \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $
L'équation caractéristique associée s'écrit : $ \displaystyle x^2+k^2 = 0 $
Le déterminant de cette équation vaut : $ \displaystyle \Delta = -4k^2 < 0 $
La solution est donc complexe et s'écrit sous la forme : $ \displaystyle \phi(x) = A\mathrm{e}^{(-ikx)}+B\mathrm{e}^{(ikx)} $
On peut déterminer les constantes A et B à l'aide des conditions aux limites:
- $ \displaystyle \dfrac{\partial \phi}{\partial x}(x=0) = ik(2-\phi(x=0) \Leftrightarrow -ikA+ikB = ik(2-A-B) \Leftrightarrow B = 1 $
- $ \displaystyle \dfrac{\partial \phi}{\partial x}(x=l) = 0 \Leftrightarrow --ikA\mathrm{e}^{(-ikL)}+ikB\mathrm{e}^{(ikL)} = 0 \Leftrightarrow A = \mathrm{e}^{(2ikL)} $
On a donc : $ \displaystyle h(x,t) = Re(\phi(x,t)) = cos(k(2L-x) - \omega t) $
Solution par méthode d'homotopie
On procède de la même manière que pour la cas 1 en trouvant $ \displaystyle /phi $ \displaystyle aux différents ordres.
- Ordre 0
On a pour ce cas p = 0 On a alors la relation : $ \phi_{0,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2} = 0 $
$ \displaystyle \Leftrightarrow \phi = Ax+B $ A l'aide des conditions aux limites:
- $ \displaystyle \dfrac{\partial \phi_0}{\partial x}(x=0) = ik(2-\phi_0(x=0)) \Leftrightarrow ik(2-B) = 0 \Leftrightarrow B = 2 $
- $ \displaystyle \dfrac{\partial \phi_0}{\partial x}(x=L) = 0 \Leftrightarrow A = 0 $
On a donc $ \phi_0 = 2 $
- Ordre 1
On a pour ce cas p = 1 On a alors la relation : $ \displaystyle \phi_{1,xx} = \dfrac{\partial^2 \phi_1}{\partial x^2}+k^2\phi_0 = 0 \Leftrightarrow \phi_1 = -k^2x^2+Cx+D $
A l'aide des conditions aux limites :
- $ \displaystyle \dfrac{\partial \phi_1}{\partial x}(x=0) = ik\phi_1(x=0) \Leftrightarrow ikD = 2k^2L \Leftrightarrow D = 2ikL $
- $ \displaystyle \dfrac{\partial \phi_1}{\partial x}(x=L) = 0 \Leftrightarrow C = 2k^2L $
On a donc $ \displaystyle \phi_1 = -k^2x^2+2k^2Lx+2ikL $
Troisième Cas
Pour ce troisième cas on se place dans un domaine de longueur L avec un fond dont la pente est constante. Nous avons deux conditions pour ce modèle qui sont $ \phi $ = 1 à l'entrée et $ \phi_{x} = ik\phi $ à la sortie.
On pose aussi les conditions suivantes :
- k non constant : $ \displaystyle k(x) = k_0\sqrt{\dfrac{H_0}{H(x)}} = k_0\sqrt{\dfrac{H_0}{H_0 - sx}} $
- $ \displaystyle CC_g = gH(x) $
On obtient alors pour l'équation de Berkhoff :
$ \displaystyle H(x)\frac{\partial^2 \phi}{\partial x^2} + (-s)\frac{\partial \phi}{\partial x} + k_0^2H_0 \phi = 0 $
Solution analytique
A l'aide du changement de variable $ z(x) = H_0 - sx $ on va obtenir une équation de type bessel et par identification on pourra obtenir $ \alpha $.
On a alors :
$ \displaystyle z(x)\frac{\partial^2 \phi}{\partial z^2} + \frac{\partial \phi}{\partial z} + \frac{k_0^2H_0}{s^2} \phi = 0 \Leftrightarrow \alpha^2 = \frac{k_0^2H_0}{s^2} $
Quatrième Cas
Ce cas ci traite d'une vague sphérique générée par une source sinusoïdale périodique. La source est appliquée autour d'un cercle de rayon $ r_0 $ centré dans un domaine circulaire de rayon R, avec sortie libre de l'onde en r = R. Dans ce cas-là, l'équation de Berkhoff se simplifie en équation de Helmholtz, et peux s'exprimer en coordonnées polaires. on a ainsi les conditions suivantes :
- $ \displaystyle \phi_rr + \frac{1}{r}\phi_r + k^2\phi = 0 $ (symétrie de révolution, donc indépendant de $ \theta $ )
- $ \displaystyle \phi(r=r_0) = 1 $
- $ \displaystyle \phi_r(r=R) = ik \phi(r=R) $
Solution analytique
Solution par méthode d'homotopie
On procède de la même manière que pour la cas 1 en trouvant $ /phi $ aux différents ordres.
- Ordre 0
On a pour ce cas p = 0 On a la relation : $ \displaystyle \phi_0,rr = 0 \Leftrightarrow \phi_0 = Ar+B $
A l'aide des conditions aux limites :
- $ \displaystyle \phi_0(r=r_0) = 1 \Leftrightarrow Ar_0+B = 1 $
- $ \displaystyle \phi_r(r=R) = ik \phi(r=R) \Leftrightarrow A = ik(AR+B) $
On a donc : $ \displaystyle A = \frac{ik}{1+ik(r_0-R)} $ et $ B = \frac{1-ikR}{1+ik(r_0-R)} $
On en déduit alors : $ \displaystyle \phi_0 = \frac{ik}{1+ik(r_0-R)} r + \frac{1-ikR}{1+ik(r_0-R)} $
- Ordre 1
On a pour ce cas p = 1
 S'abonner à un flux RSS
S'abonner à un flux RSS