Mécanique des fluides numérique / MFN (HU)

Traduction anglaise : Computational Fluid Dynamics / CFD

Dernière mise à jour : 18/05/2022

mot en chantier

Ensemble de méthodes numériques permettant de représenter différents phénomènes physiques d'écoulement de fluides, décrits par des équations différentielles ou des équations aux dérivées partielles (EDP) fortement non-linéaires et parfois couplées à d’autres équations (Magnétohydrodynamiques, Turbulence, Milieux poreux, etc.) ; dans le domaine de l'hydraulique, la MFN concerne en particulier la résolution des équations de Navier-Stokes pour une géométrie donnée.

Principes

Le principe de base consiste à transformer un phénomène représenté par des équations différentielles ou des EDP sur un domaine physique continu par un système d'équations algébriques prenant des valeurs sur un domaine discret, puis à résoudre ces équations algébriques en utilisant un solveur plus ou moins générique mis en œuvre par un logiciel adéquat. Pour ceci différentes étapes sont nécessaires :

• choix d'une formulation et, par association, d'une méthode de mise en équations ; trois méthodes, que l'on peut coupler, sont utilisables :

• approximation directe des dérivées des variables par des opérateurs algébriques et méthode des différences finies ;
• approximation directe des variables (forme intégrale) par des opérateurs algébriques en utilisant la formulation variationnelle et méthode des éléments finis (formulation faible) ;
• approximation directe des variables (forme intégrale) par des opérateurs algébriques et méthode des volumes finis (formulation forte).

• délimitation du domaine d'étude et maillage de ce domaine ;
• construction des équations algébriques correspondant aux EDP sur le domaine discret ;
• choix des conditions aux limites et construction des équations algébriques correspondantes sur les différents "bords" du domaine d'étude de façon à ce que le nombre d'équations soit égal au nombre d'inconnues ;
• utilisation d'un solveur pour résoudre le système d'équations algébriques sur le maillage choisi.

Choix de la méthode

La plupart des logiciels utilisent la méthode des volumes finis pour discrétiser les opérateurs dans l'espace. Cette méthode consiste en effet à écrire, sur chaque volume élémentaire, que la variation interne de la grandeur considérée (masse, énergie, quantité de mouvement) est égale à la somme des flux qui traversent sa frontière ; elle est donc conservative par construction. Si nécessaire (dans le cas des phénomènes évolutifs), la méthode des différences finies est alors utilisée en complément pour discrétiser les dérivées premières sur le temps.

Choix du maillage

Le maillage a pour but de subdiviser le domaine spatial de calcul en un grand nombre de petits éléments appelés cellules. Ces cellules sont des segments dans le cas 1D, des surfaces dans le cas 2D ou des volumes dans le cas 3D. Dans le cas de la méthode des volumes finis les grandeurs sont calculées en un point particulier de chacune des mailles appelé centre. La méthode des volumes finis est très souple et les cellules peuvent prendre des formes quelconques ; de plus leurs formes, comme leur taille, peuvent varier selon la position. Le maillage doit cependant vérifier deux conditions :

• il doit recouvrir totalement le domaine ;
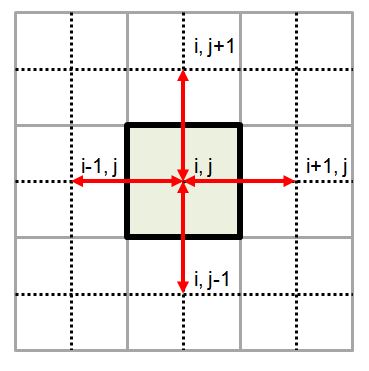
• il doit être "admissible", c'est à dire que chaque cellule doit posséder un centre tel que chaque ligne joignant ce centre aux centres de chacune des cellules voisines doit obligatoirement être normal à la frontière entre ces cellules et passer par cette frontière (figure 1).

Figure 1 : Cellule admissible et cellule non admissible.

Dans le cas d'un maillage régulier, on parle de maillage structuré, par exemple constitué de carrés juxtaposés de même taille pour un problème à deux dimensions (figure 2), la construction du maillage est très simple.

Figure 2 : Exemple de maillage carré régulier ; dans ce cas les flux reliant les centres de cellules contiguës sont obligatoirement normaux à la frontière entre ces cellules.

Cependant de type de maillage pose également des problèmes :

• Il est difficile de représenter des ouvrages dont la géométrie est compliquée ;
• la taille des cellules est obligatoirement la même partout ce qui, soit limite la précision du maillage, soit conduit à un très grand nombre de cellules.

On utilise donc souvent des maillages non structurés en utilisant des procédés de construction spécifiques, par exemple triangulation de Delaunay ou polygones de Voronoï (Scheid, 2017) (figure 2).

Figure 3 : Exemple de maillage non structuré admissible constitué de polygones convexes particuliers, dits de Voronoï ; Source : Scheid (2017).

Dans la pratique les logiciels sont généralement dotés de fonctions spécifiques (mailleurs) permettant de construire le maillage de façon assistée. Cette étape reste cependant très délicate car elle nécessite de trouver un équilibre entre la précision attendue et le temps de calcul. Ce compromis impose généralement de densifier le maillage dans les zones où les grandeurs évoluent rapidement (ce qui suppose que l'on a une idée a priori de l'allure du phénomène) (figure 4).

Figure 4 : Exemple de maillage parallélépipédique à 3 dimensions avec une taille de cellules différentes selon les zones ; l'objectif est ici de représenter les écoulements à surface libre dans une défluence (départ de ; Source : Monplot (2014).

domaines d'utilisation en hydrologie urbaine

Pour les écoulements à surface libre, la difficulté principale est la détermination claire de la séparation entre les fluides eau et air, c'est à dire la ligne d'eau.

Bibliographie :

• Monplot, A. (2014) : Modélisation tridimensionnelle des écoulements en réseau d’assainissement ; Évaluation des modèles RANS à travers l’étude des écoulements au droit d’ouvrages spéciaux ; thèse de doctorat INSA de Lyon ; 206p. ; disponible sur https://www.theses.fr/2014ISAL0125.pdf.
• Scheid, J.-F. (2017) : Volumes finis ; Méthodes numériques avancées pour la résolution des EDP ; cours de Master 2 ; IMOI, Université de Lorraine ; 67p. ; disponible sur http://scheid.perso.math.cnrs.fr/Enseignement/polyVF2017_18.pdf.