Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/trinome2: BUCHER-GIORGI-LOTHON

Contextualisation

Le thème d’étude est la quantification de l’impact des houles sur le littoral. La probabilité de survenue d’événements extrêmes va considérablement augmenter à cause du changement climatique et leurs impacts sur le littoral va provoquer des désordres sur les secteurs les plus vulnérables entraînant le recul du trait de côte, la disparition de propriétés et d’ouvrages et des déplacements de populations.

Modèle de Berkhoff

Dans le but de modéliser la houle, nous allons utiliser le modèle de Berkhoff. Ce modèle est utilisé pour prédire la propagation et l'impact des vagues sur les côtes. C'est un modèle bi-dimensionnel qui a pour expression:

$ \frac{\partial }{\partial x_i}(CC_g \frac{\partial \phi}{\partial x_i})+ k^2CC_g\phi = 0 $ avec $ i = {1,2} $

On note:

$ \phi $ : le potentiel de vitesse

$ C $ : la célérité de l'onde

$ C_g $ : la célérité de groupe des vagues

$ k $ : le nombre d'onde

$ H $ : la hauteur de la houle

Il se base sur un grand nombre d'hypothèses:

- le fluide est considéré conne étant parfait, incompressible et irrotationnel

- le fond est fixe et imperméable

- la hauteur de la houle est faible par rapport à sa longueur d’onde et à la profondeur

- les sollicitations atmosphériques à la surface libre sont négligées

Nous nous plaçons dans le cadre des ondes longues, ce qui signifie que $ C = C_g = \sqrt{gH} $. L'équation devient alors:

$ \frac{\partial }{\partial x_i}(H \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 $

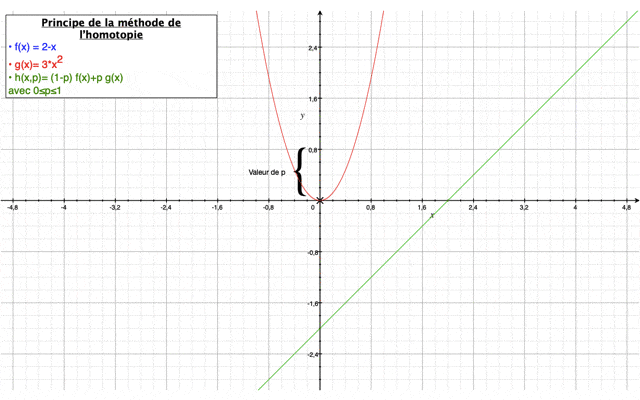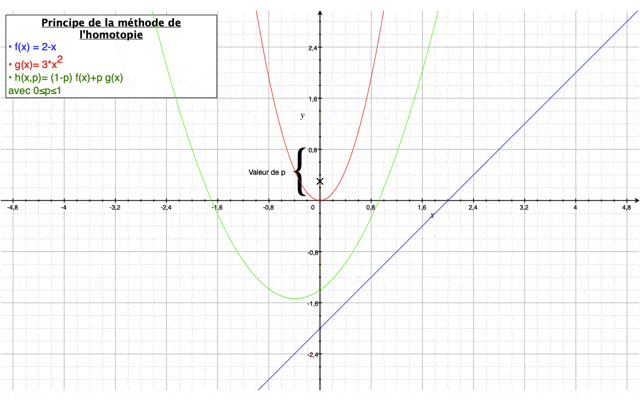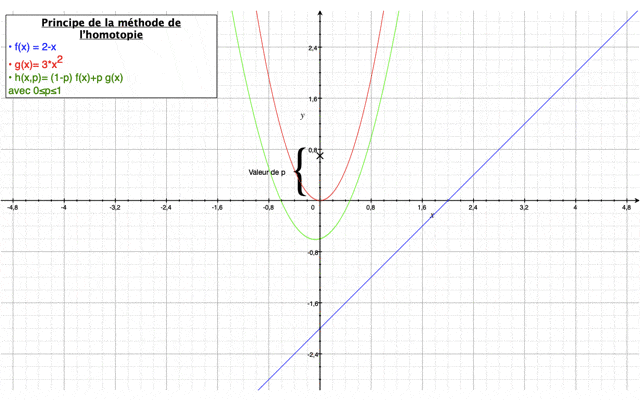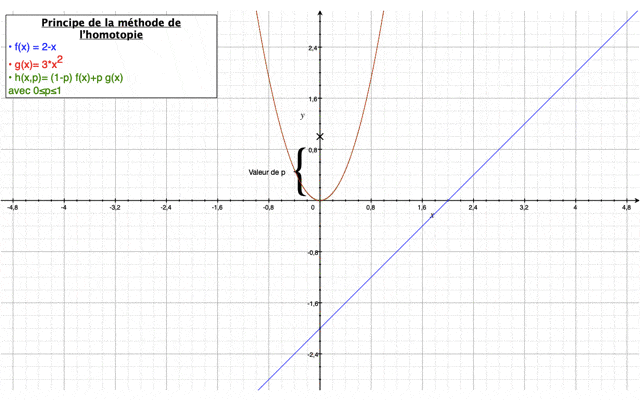
Méthode homotopique

Tout d'abord, la méthode de l'homotopie a pour but de résoudre des équations différentielles et des intégrales. Elle permet à partir d’une solution connue relativement simple de converger vers une solution complète grâce à un paramètre p qui varie entre 0 et 1 et qui assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre.

Elle est définie comme suit :$ (1−p)[L(U(x,t);p)−L(u0(x,t))]+cH(p)[L(U(x,t);p)−N(U(x,t),p)−f(x)] $

avec L est un opérateur linéaire, N un opérateur non-linéaire, f les termes complémentaires de l’équation et u0 est une estimation initiale de la solution.

Dans notre cas, on prendra $ H(p)=p $

Ci-dessous, est présentée dans une vidéo, le principe général de la méthode.

Étude cas

Cas n°1 : canal uniforme unidimensionnel plat de longueur L avec sortie libre amont

Résolution : Méthode analytique

Dans le cadre de l'hypothèse canal uniforme plat, on a $ H = constante $. On a alors :

$ \frac{\partial }{\partial x_i}(H \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 \Leftrightarrow H\frac{\partial }{\partial x_i}( \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 \Leftrightarrow \cancel{H}\frac{\partial }{\partial x_i}( \frac{\partial \phi}{\partial x_i})+ k^2\cancel{H}\phi = 0 \Leftrightarrow \frac{\partial^2 \phi}{\partial x_i^2}+ k^2\phi = 0 $

On obtient alors une équation différentielle du second degré sans second membre à résoudre.

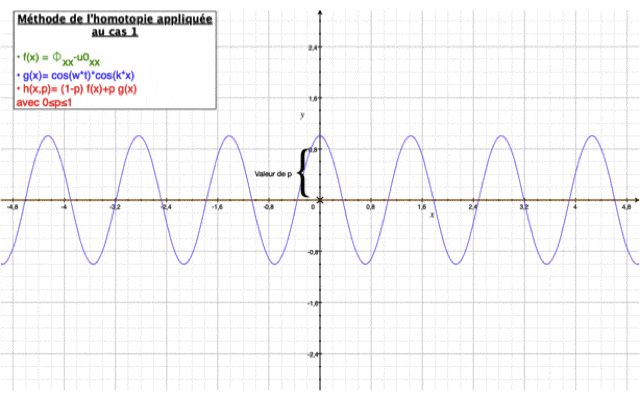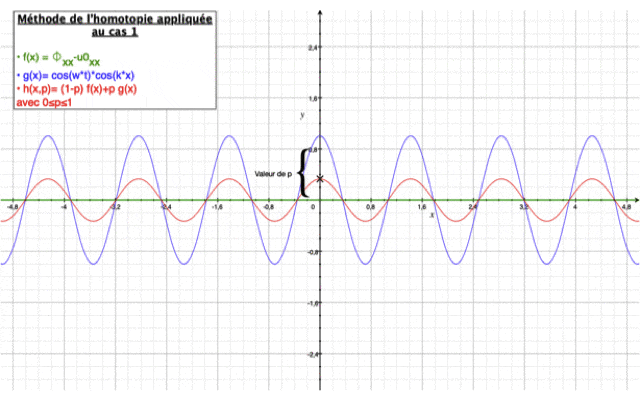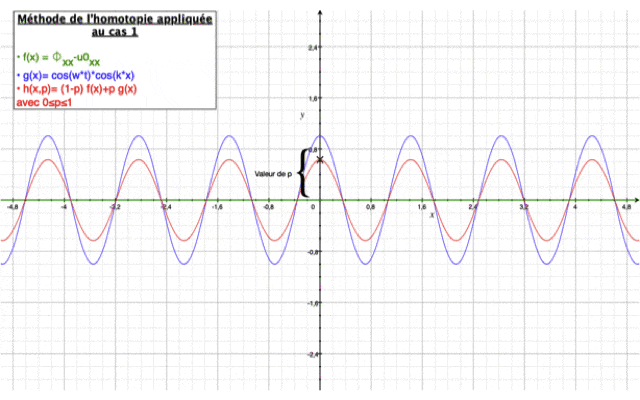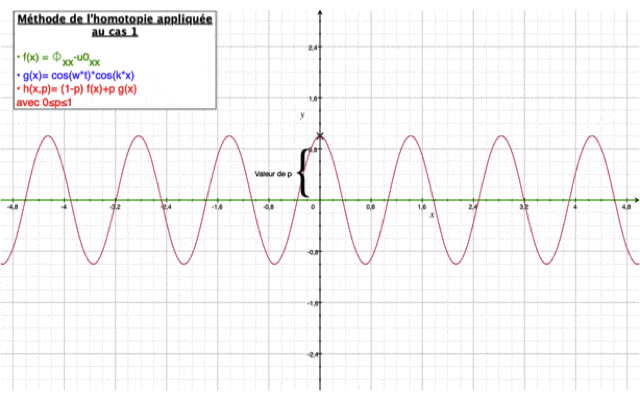
$ \phi(x)=A\cos(kx)+B\sin(kx) $

avec $ k = \frac{\omega}{c} \Rightarrow k = \frac{2\pi}{T\sqrt{gH_0}} $

D'après les conditions initiales, on a :

$ \bullet \phi(0)=1 \Rightarrow A=1 $

$ \bullet \phi(L)=ik\phi \Rightarrow B= i $

On en déduit l'expression de $ \phi $ :

$ \phi(x)= \cos(kx)+i\sin(kx) $

La hauteur de houle est :

$ H =  \frac{Re(\phi)}{ |\phi|}= \cos(kx)  $

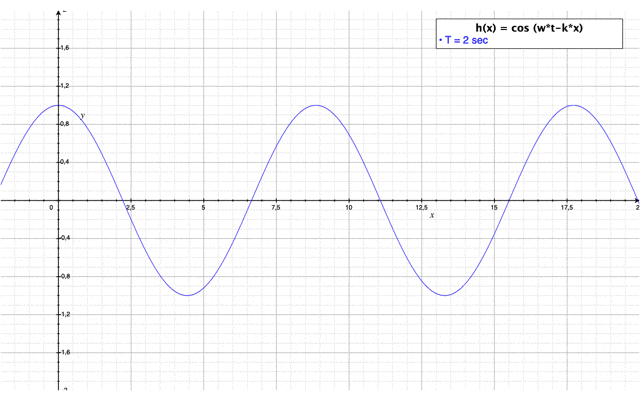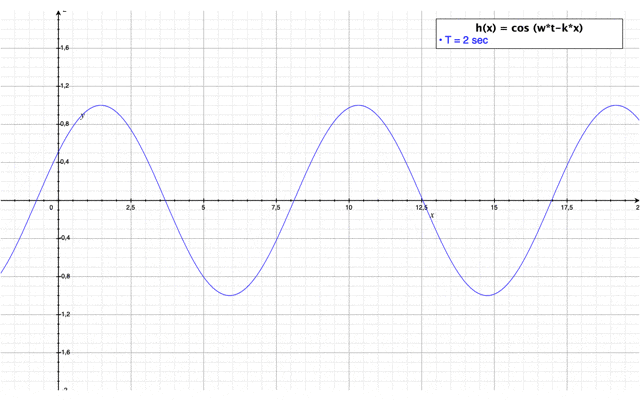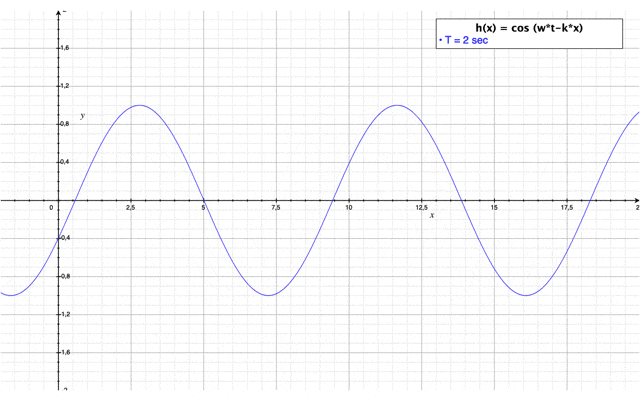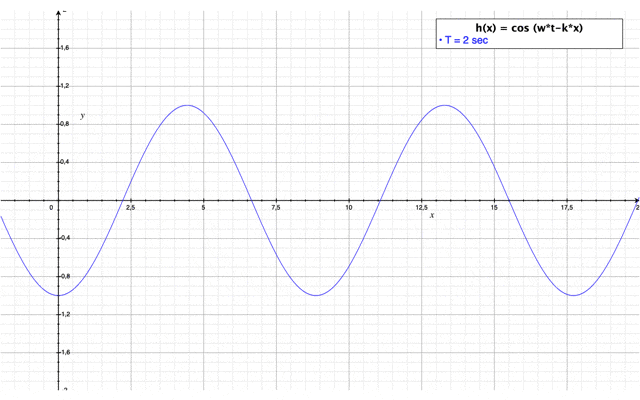
avec une évolution dans le temps : $ \color{blue}h(x,t)=\cos(wt-kx) $

Résolution par la méthode homotopique

La relation d'homotopie est : $ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $

On a par ailleurs :

• $ \phi(x)=\sum_{k=0}^\infty p^n \phi_n $

• et sa dérivée seconde $ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $

Ordre 0 :

L'équation devient à l'ordre 0 : $ \phi_{0,xx}=0 $

donc $ \phi_0(x)=A_0x+B_0 $ avec $ A_0 $ et $ B_0 $ deux constantes réelles.

En appliquant les conditions initiales, on obtient :

$ \bullet x=0, \phi(x=0)=1 $ donc $ B_0= 1 $

$ \bullet x=L, \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(x=L) $ donc $ A_0=\frac{ik}{1-ikL} $ et pour un résultat réaliste on pose $ kL=1 $, on a alors : $ A_0=\frac{i}{L(1-i)} $

Soit finalement, $ \phi_0(x)=1+\frac{i}{L(1-i)}x $

Ordre 1 :

L'équation devient à l'ordre 1 : $ \phi_{1,xx}+k^2 \phi_0=0 $

donc $ \phi_1(x)=-k^2(\frac{i}{L(1-i)}\frac{x^3}{6}+\frac{x^2}{2}+A_1x+B_1) $

D'après les conditions initiales, on a : $ A_1=L(1+e^{i(\frac{x}{L}-1)}-(1+\frac{i}{(1-i)})) $ et $ B_1=-L^2 $

Soit finalement, $ \phi_1(x)=-\frac{1}{L^2}(\frac{i}{L(1-i)}\frac{x^3}{6}+\frac{x^2}{2}+L(1+e^{i(\frac{x}{L}-1)}-(1+\frac{i}{(1-i)})x)+1 $

Ordre 2 : $ \phi_{2,xx}+k^2 \phi_1=0 $

Ordre 3 : $ \phi_{3,xx}+k^2 \phi_2=0 $

.

.

.

Ordre N : $ \phi_{N,xx}+k^2 \phi_{N-1}=0 $

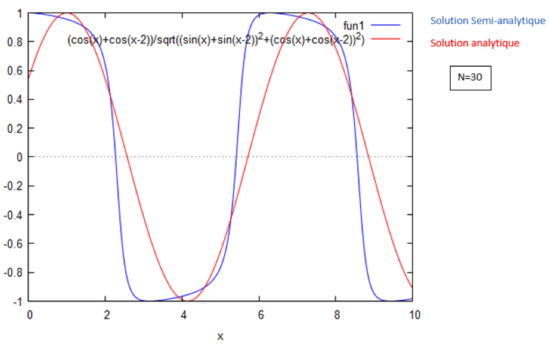
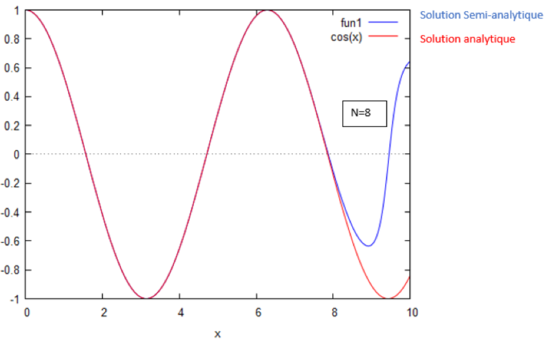
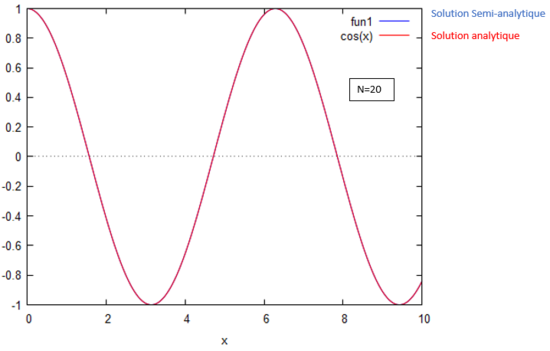
Les deux images ci-dessous montre la solution homotopique obtenue en fonction du nombre d'itérations effectuées superposée à la solution analytique.

Ci-dessous cette vidéo illustre le principe de la méthode appliquée au Cas n°1

Représentation animée du modèle

Valeurs attribuées pour le régime de houle :

$ H_0=2 m $

$ T=2 s $

$ c=4.43 m.s^{-1} $

$ k=0.709 m^{-1} $

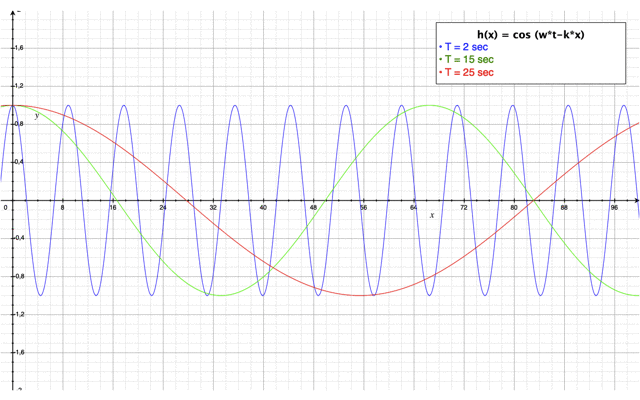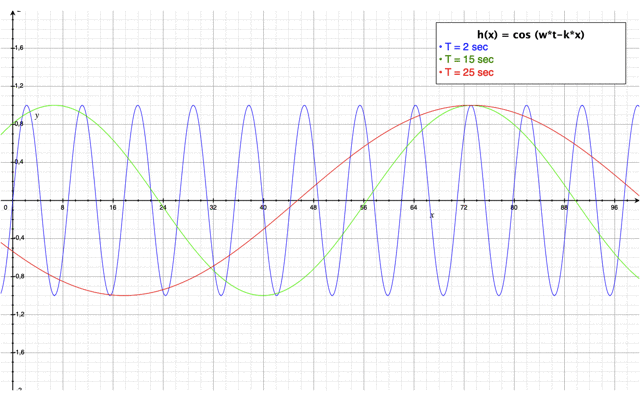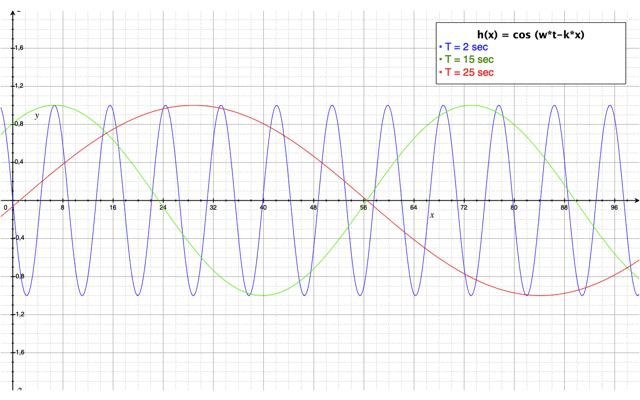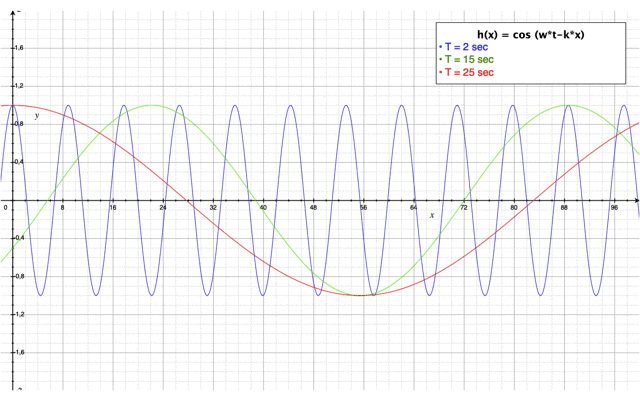
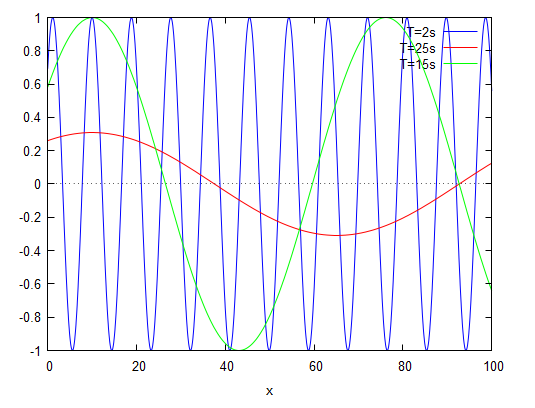
Etude de sensibilité de la période T de la houle

Il faut savoir que les trains de vagues peuvent avoir des périodes très différentes par rapport aux conditions météorologiques de leur formation. C'est l'impact de cette période que nous nous proposons d'étudier dans cette section. La vidéo ci-dessus permet de visualiser l'impact de la période de la houle sur des paramètres caractéristiques de la houle comme sa cambrure ou encore sa hauteur.

Dans ce cas, la hauteur de la houle n'est pas impactée par la période de la houle. Néanmoins, on remarque que lorsque la période de la houle augmente la cambrure de la vague diminue. En fait, les vagues transportent de l'énergie qui est proportionnelle à la période et la longueur d'onde de la houle. Les vagues dont la période est courte se déplacent moins vite. Ainsi, elles s'amortissent par dissipation d'énergie et disparaissent rapidement. Alors que les vagues ayant une période longue se déplacent plus vite. Ainsi, elles peuvent parcourir des distances plus longues. Ces vagues sont généralement puissantes et régulières. Ce sont ces vagues qui vont atteindre les côtes du littoral et avoir un impact important sur celles-ci.

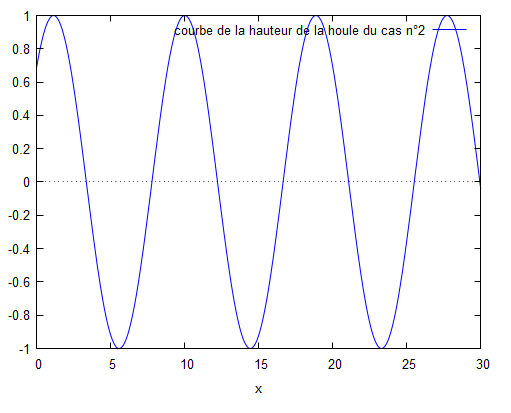
Cas n°2 : canal uniforme unidimensionnel réflexion totale amont

Résolution : Méthode analytique

L'équation différentielle est la même que dans le cas n°1, soit $ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $ , seules les conditions initiales diffèrent.

On a $ \phi(x)=Ae^{-ikx}+Be^{ikx} $ avec $ k = \frac{\omega}{c} \Rightarrow k = \frac{2\pi}{T\sqrt{gH_0}} $

D'après les conditions initiales, on obtient :

$ \bullet $ En aval : $ \phi_x=ik(2-\phi) \Rightarrow B=1 $

$ \bullet $ En amont : $ \phi_x=0 \Rightarrow A = e^{2ikL} $

On en déduit l'expression de $ \phi $ :

$ \phi(x)= e^{ik(2L-x)}+e^{ikx} = \cos(2kl-kx)+i\sin(2kL-kx)+\cos(kx)+i\sin(kx) $

La hauteur de la houle est donc :

$ H =\frac{Re(\phi)}{|\phi|}=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}}  $

avec une évolution dans le temps : $ \color{blue}h(x,t)=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}}*\cos(wt) $

Résolution par la méthode homotopique

La relation d'homotopie est la même que pour le cas n°1, seules les conditions initiales diffèrent (comme vu plus haut).

Ordre 0 :

L'équation devient à l'ordre 0 : $ \phi_{0,xx}=0 $ (avec $ u_0 = 0 $)

donc $ \phi_0(x)=A_0x+B_0 $ avec $ A_0 $ et $ B_0 $ deux constantes réelles.

En appliquant les conditions initiales, on obtient :

$ A_0= 0 $ et $ B_0= 1 $.

On a alors : $ \phi_0(x)= 1 $

Ordre 1 :

L'équation devient à l'ordre 1 : $ \phi_{1,xx}+k^2 \phi_0=0 $

donc $ \phi_1(x)=-k^2{x^2}+A_1x+B_1 $ avec $ A_1 $ et $ B_1 $ deux constantes réelles.

D'après les conditions initiales, on obtient :

$ A_1= 2k^{2}L $ et $ B_1= -(2+2ikL) $

soit $ A_1= 2kL $ et $ B_1= -(2+2i) $ avec $ kL= 1 $

Finalement, on a : $ \phi_1(x)=-k^2{x^2}+2kLx-2-2i $

Etude de sensibilité de la période T de la houle

Comme précédemment, pour ce cas, nous allons évaluer l'impact de la période sur les paramètres caractéristiques de la houle à savoir la cambrure des vagues et leur hauteur.

En ce qui concerne la cambrure de la houle, elle est impactée de la même manière que dans le cas précédent à savoir que plus la période est grande et plus la cambrure de la houle est faible. En revanche, contrairement au cas précédent, la période de la houle a une influence sur la hauteur de celle-ci. Ainsi, plus la période est grande et plus la hauteur de la houle est petite. La hauteur de la vague est un paramètre important puisqu'elle mesure l'amplitude de la houle. Une amplitude moins élevée traduit une quantité d'énergie transportée moins importante. Ainsi, dans ce cas, étant donné que la hauteur de la vague a diminué, la houle aura un impact moins important que dans le cas précédent.

Cas n°3 : Domaine monodimensionnel de longueur L avec pente du fond constante

Résolution : Méthode Analytique

Le modèle de Berkhoff nous donne :

$ \frac{\partial}{\partial x}(H\frac{\partial\phi}{\partial x})+k^2H\phi=0 $

La hauteur a pour expression :

$ H(x)=H_0-sx $ avec s la pente du fond du bassin

On a alors :

$ (H_0-sx)\frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k^2(H_0-sx)\phi(x) $

En réalisant le changement de variable suivant :$ X=H_0-sx $

On obtient l'équation : $ s^2X\frac{\partial^2\phi}{\partial X^2}+s^2X\frac{\partial\phi}{\partial X}+k^2X\phi(X)=0 $

En divisant par $ s^2 $ puis en multipliant par $ X $

On obtient l'équation de Bessel suivante :

$ X^2\frac{\partial^2\phi}{\partial X^2}+X\frac{\partial\phi}{\partial X}+\Big(\frac{k}{s}\Bigr)^2X^2\phi(X)=0 $

La solution est de la forme :

$ \phi(X)=AJ_0(X)+BY_0(X) $ avec $ J_0(X)=\sqrt{\frac{2}{\pi X}}\cos(X-\frac{\pi}{4}) $ et $ Y_0(X)=\sqrt{\frac{2}{\pi X}}\sin(X-\frac{\pi}{4}) $

c'est à dire : $ J_0(x)=\sqrt{\frac{2}{\pi (H_0-sx)}}\cos(H_0-sx-\frac{\pi}{4}) $ et $ Y_0(x)=\sqrt{\frac{2}{\pi(H_0-sx)}}\sin(H_0-sx-\frac{\pi}{4}) $

Avec les conditions initiales, on exprime les constantes A et B :

$ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

Résolution par la méthode homotopique

La relation d'homotopie est : $ (1-p)(\phi_{xx}-u_{0,xx})+p(mx\phi_{xx}-m\phi_x(x)+k^2(1-mx)\phi(x))=0 $ avec $ m=\frac{s}{H_0} $

On a par ailleurs :

• $ \phi=\sum_{k=0}^\infty p^n \phi_n $

• et sa dérivée première $ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $

• et sa dérivée seconde $ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $

Pour la suite, on prendra $ u_{0,xx}= 0 $ afin de simplifier les calculs.

Ordre 0 :

L'équation devient à l'ordre 0 : $ \phi_{0,xx}= 0 $

En appliquant les conditions initiales, on obtient :

$ \bullet x=0, \phi(x=0)=1 $ donc $ B_0= 1 $

$ \bullet x=L, \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(x=L) $ donc $ A_0=\frac{ik}{1-ikL} $ et donc pour $ kL=1 $, on a $ A_0=\frac{i}{L(1-i)} $

Soit finalement, $ \phi_0(x)=1+\frac{i}{L(1-i)}x $

Ordre 1 :

L'équation devient à l'ordre 1 : $ \phi_1,xx-mx\phi_{0,xx}-m\phi_0x+k^2(1-mx)\phi_0=0 $

Cas n°4 : Domaine monodimensionnel de longueur L avec pente du fond exponentielle et sortie libre amont

Résolution : Méthode analytique

Expression de la hauteur

$ H(x)=H_0\mathrm{e}^{-sx} $

L'équation de Berkhoff devient : $ H_0\mathrm{e}^{-sx}\frac{\partial^2\phi}{\partial x^2}-sH_0\mathrm{e}^{-sx}\frac{\partial\phi}{\partial x}+k_0^2H_0\mathrm{e}^{-sx}\phi=0 $

$ H_0\mathrm{e}^{-sx}\Big(\frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k_0^2\phi\Bigr)=0 $

$ H_0\mathrm{e}^{-sx}\neq0 $

Donc on obtient l'équation suivante : $ \frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k_0^2\phi=0 $

L'équation caractéristique associée est de la forme :$ x^2-sx+k_0^2=0 $

La forme des solutions dépend du signe de $ \Delta $: $ \Delta=s^2-4k_0^2 $

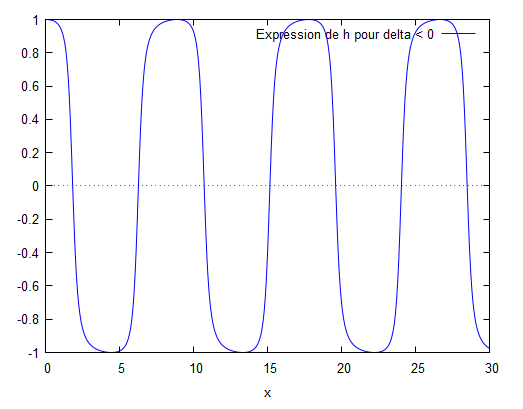
$ \bullet \Delta<0 $; l'équation est de la forme :$ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[c_1\cos\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)+c_2\sin\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)] $

$ \bullet \Delta=0 $; l'équation est de la forme : $ \phi(x)=(c_1x+c_2)\mathrm{e}^{\frac{s}{2}x} $

$ \bullet\Delta>0 $ ; l'équation est de la forme : $ \phi(x)=c_1\mathrm{e}^{\frac{s-\sqrt{s^2-4k_0^2}}{2}x}+c_2\mathrm{e}^{\frac{s+\sqrt{s^2-4k_0^2}}{2}x} $

Avec les conditions initiales, on exprime les constantes $ c_1 $ et $ c_2 $ :

$ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $

$ \bullet \Delta<0 $ : on note $ u=\frac{s}{2} $ et $ v=\frac{\sqrt{s^2-4k_0^2}}{2} $

$ c_1=1 $ et $ c_2=\frac{v\sin(vL)+\cos(vL)(ik-1)}{v\cos(vL)+\sin(vL)(1-ik)} $

L'équation s'écrit : $ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[\cos\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)+\frac{v\sin(vL)+\cos(vL)(ik-1)}{v\cos(vL)+\sin(vL)(1-ik)}\sin\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)] $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

$ T=2s $

$ H_0=2m $

$ k=0.709m^{-1} $

$ c=4.43m/s $

$ s=0.01 $

$ \bullet \Delta=0 $ :

$ c_1=\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL} $ et $ c_2=1 $

L'équation s'écrit : $ \phi(x)=(\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL}x+1)\mathrm{e}^{\frac{s}{2}x} $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

$ s=1.418 $

$ k=0.709m^{-1} $

$ c=4.43m/s $

$ T=2s $

$ H_0=2m $

$ \bullet\Delta>0 $ : on note $ x_1=\frac{s-\sqrt{s^2-4k_0^2}}{2} $ et $ x_2=\frac{s+\sqrt{s^2-4k_0^2}}{2} $

$ c_1=1-\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}} $ et $ c_2=\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}} $

L'équation s'écrit : $ \phi(x)=\Big(1-\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}}\Bigr)\mathrm{e}^{\frac{s-\sqrt{s^2-4k_0^2}}{2}x}+\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}}\mathrm{e}^{\frac{s+\sqrt{s^2-4k_0^2}}{2}x} $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

$ s=2 $

$ k=0.709m^{-1} $

$ c=4.43m/s $

$ T=2s $

$ H_0=2m $

Résolution par la méthode homotopique

L'équation de l'homotopie est : $ (1-p)[\phi_{xx}-u0_{xx}]+p[\phi_{xx}-s\phi_x+k_0^2\phi]=0 $

$ \phi=\sum_{k=0}^\infty p^n \phi_n $

$ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $

$ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $

Ordre 0 : $ \phi_{0,xx}-u0_{xx}=0 $

Ordre 1 : $ \phi_{1,xx}+u0_{xx}-s\phi_{0,x}+k_0^2\phi_0=0 $

Ordre 2 : $ \phi_{2,xx}-s\phi_{1,x}+k_0^2\phi_1=0 $

.

.

.

Ordre N : $ \phi_{N,xx}-s\phi_{N-1,x}+k_0^2\phi_{N-1}=0 $

Analyse des résultats et limites du modèle

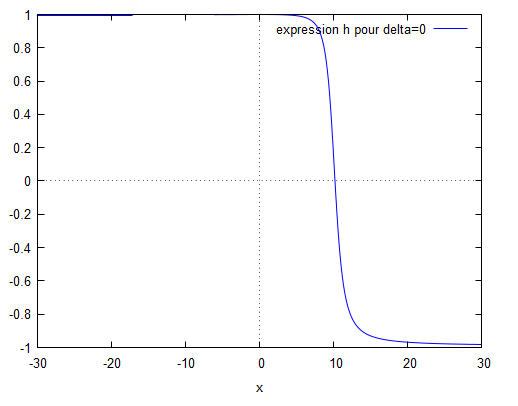
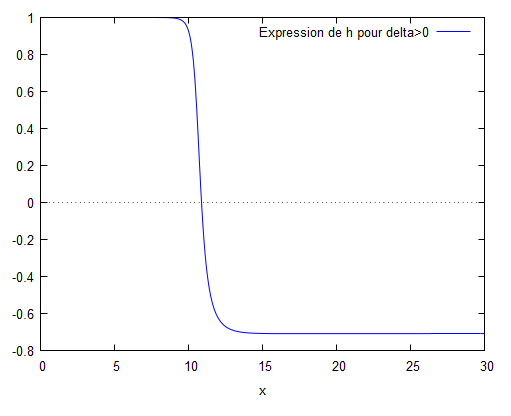
Le modèle de Berkhoff a permis de tracer l'évolution de la hauteur des vagues en fonction de la position. Les différents modèles montrent que la houle est régulière quelque soit les paramètres du fond sauf pour le cas n°4 où nous observons une hauteur de vague qui finit par tendre vers 0 pour delta nul et delta positif. On peut donc conclure que pour le cas n°4, seul le cas ou delta est négatif peut être observable.

Le modèle permet d'observer qualitativement les cambrures des vagues selon les différents cas. Il permet aussi d'analyser l'influence de la période de la houle sur les côtes. En effet, la houle transporte de l'énergie qui est proportionnelle à sa période, ce qui permet de déterminer son impact sur les côtes.

Cependant, pour l'étude de nos cas, nous nous sommes placés dans un domaine monodimensionnel or le modèle de Berkhoff est bidirectionnel. Il aurait donc fallu prolonger l'étude pour un domaine bidirectionnel pour s'approcher davantage de la réalité.

Le modèle de Berkhoff nécessite de nombreuses hypothèses simplificatrices comme énoncé dans la section "modèle de Berkhoff", comme notamment le fait que les sollicitations atmosphériques à la surface soient négligées or nous savons que le vent est un paramètre important qui influence la taille, le type de la vague et leur vitesse. Dans le but d'améliorer le modèle, il serait intéressant d'étudier la vitesse et la durée du vent, l'état d'origine à la surface de la mer et également considéré que le fluide (la mer) n'est pas parfait.