Wikibardig:Trinôme 5 : ZARO Pauline, TOURNEMIRE Clara, MORELL Maxime

Contexte

Le réchauffement climatique est un enjeu planétaire et une préoccupation pour tous les citoyens du monde. La remontée du niveau des océans en est une des nombreuses conséquences. L'élévation du niveau de la mer cause des dommages sur les aménagements côtiers et constitue un danger pour l'ensemble des populations. Dans ce projet, nous chercherons à modéliser l'impact du changement climatique sur le littoral. Notre étude se porte plus précisément sur la quantification de l'impact de la houle sur le littoral.

Les équations obtenues seront résolues par une méthode analytique et une méthode semi-analytique: l'homotopie.

Hypothèses du modèle

La houle est modélisée comme une onde régulière monochromatique. On considère un fluide parfait, incompressible et irrotationnel. les sollicitations atmosphériques à la surface libre (gradient de pression et vent ) sont négligeables.

Modèle de Berkhoff

Afin de modéliser la houle, nous utiliserons le modèle de Berkhoff, son écriture en domaine bidimensionnel est le suivant :

$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $

où $ \phi $ est le potentiel, k est le nombre d’onde fonction de la profondeur H et de la fréquence $ \omega $ (T est la période), par la relation implicite $ \omega^2=gk \tanh(kH) $ , C est la célérité de l’onde, Cg est la célérité de groupe des vagues.

Comme nous nous plaçons en domaine des ondes longues on peut écrire : $ C=C_g=\sqrt{gH} $.

D'autre part, l'évolution dans le temps de la hauteur de houle est donnée par : $ h(x,t)=\Re \left (\phi e^{-i\omega t} \right ) $.

La méthode d'homotopie

La méthode d'homotopie permet de calculer la solution d'une équation non linéaire de manière semi-analytique. Elle s'appuie sur la transformation de la la solution en série de Taylor. Nous ferons varier un paramètre $ p $ entre $ 0 $ et $ 1 $, pour $ p=0 $ nous obtenons la solution initiale et lorsque $ p=1 $ nous obtenons la solution finale exacte.

La méthode d'homotopie dans le cas général s'applique sur des équations du type :

$ L(u(x)) = f(x) + N(u(x)) $ avec $ x \in \Omega $

On peut réécrire cette équation telle que :

$ (1−p)[L(U(x,t);p)−L(u_0(x,t))]+cH(p)[L(U(x,t);p)−N(U(x,t),p)−f(x)] $

avec L un opérateur linéaire, N un opérateur non-linéaire, f les termes complémentaires de l’équation et $ u_0 $ une estimation initiale de la solution.

Pour le cas n°1 on a L qui correspond au Laplacien et N qui correspond à k U(x,t) = $ phi $ f(x)=0

On obtient la formule suivante:

$ (1-p)\phi_{xx} + p*(\phi_{xx}+k^2\phi) = 0 $

Nous ferons l'hypothèse que H(p)=p.

La méthode d'homotopie sera mise en oeuvre dans le logiciel Maxima, qui est un logiciel de calcul de formel qui se prête parfaitement à une résolution semi-analytique des équations.

Élaboration et validation de la méthode d'homotopie à travers plusieurs cas simples :

Nous allons considérer 3 cas différents :
-Cas n°1 : nous considérerons un domaine unidimensionnel à fond plat de longueur L avec l'entrée en aval d'une onde unitaire $ \phi = 1 $ et avec la sortie libre de cette onde en amont caractérisée par la condition à la limite en $ x=L : \frac{d\phi}{dx}=\phi_x=ik\phi $, donc $ \phi_x(L)=ik\phi(L) $.

-Cas n°2 : nous nous plaçons dans un domaine monodimensionnel à fond plat de longueur L avec l'entrée en aval d'une onde unitaire $ \phi = 1 $ ainsi qu'une condition de flux en aval $ \phi_{x} = ik(2-\phi) $ et également réflexion totale en amont $ \phi_{x} = 0 $.

-Cas n°3 : nous sommes toujours en domaine monodimensionnel de longueur L mais cette fois-ci avec une pente de fond constante avec une entrée par l'aval $ \phi = 1 $ et aussi une sortie libre en amont $ \phi_{x} = ik\phi(L) $.

Cas n°1 : Domaine unidimensionnel avec fond plat de longueur L : sans onde réfléchie

Dans ce premier cas simple, nous allons comparer la solution trouvée par homotopie et la solution trouvée par la méthode analytique afin de valider l'utilisation de la méthode d'homotopie à la résolution de l'équation citée ci-dessus. Nous considérons un domaine unidimensionnel avec fond plat de longueur L avec l'entrée en aval d'une onde unitaire $ \phi = 1 $ et avec la sortie libre de cette onde en amont caractérisée par la condition à la limite en $ x=L : \frac{d\phi}{dx}=\phi_x=ik\phi $, donc $ \phi_x(L)=ik\phi(L) $.

On a donc :
$ x=0,\ \phi=1 $
$ x=L,\ \phi_x=ik\phi $

L'équation du modèle de Berkhoff considérée $ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $ peut se réécrire en unidimensionnel : $ \frac{d}{dx}(CC_g\frac{d\phi}{dx}) + k^2CC_g\phi=0 $. Dans ce premier cas, on peut simplifier l'équation :
-En ondes longues, on a $ C=C_g=\sqrt{gH} $
-Ici, nous avons un domaine de fond plat, à une profondeur H qui est donc constante : $ H(x)=H $.

Donc l'équation peut se réécrire : $ \phi_{xx} + k^2\phi=0 $ (équivalente à $ \frac{d^2}{dx}\phi + k^2\phi=0 $). C'est l'équation que nous allons résoudre avec la méthode analytique et la méthode d'homotopie.

Résolution analytique

$ \phi_{xx} + k^2\phi=0 $ une équation différentielle linéaire homogène d'ordre 2 à coefficients constants définie $ \forall x\in [0,L] $

L'équation caractéristique de celle ci est : $ \begin{equation} \label{EC} r^2 + k^2 = 0 \end{equation} $
$ \Longleftrightarrow r=\pm ik $
On a donc la forme de solution suivante (puisque $ \beta = \Im(r) = k $ et $ \DeclareMathOperator{\e}{e} \alpha = \Re(r) = 0 \Rightarrow \e^{\alpha x} $) : $ \phi(x) = \lambda \cos(kx) + \mu \sin(kx) $

On trouve les coefficients $ \mu $ et $ \lambda $ avec les conditions aux limites :
$ \phi(0) = \lambda = 1 $
$ \phi_x(L) = ik\phi(L) \Longleftrightarrow -k\sin (kL) + \mu k \cos (kL) = ik(\cos (kL) + \mu \sin (kL)) \Longleftrightarrow \mu = \frac{\sin(kL) + i\cos(kL)}{\cos(kL)-i\sin(kL)} $

Donc $ \phi (x) = \cos (kx) + \bigg(\frac{\sin(kL) + i\cos(kL)}{\cos(kL)-i\sin(kL)}\bigg) \sin (kx) $

Maintenant que l'on a le potentiel des vitesses $ \phi $, on va déterminer $ h $ qui est la hauteur d'eau algébrique s'ajoutant à la hauteur d'eau moyenne $ H $ constante dans ce Cas n°1. On met $ \phi $ sous forme classique $ \alpha + i\beta $ : $ \phi = \cos (kx) + \bigg(\frac{\sin(kL) + i\cos(kL)}{\cos(kL)-i\sin(kL)}\bigg) \sin (kx) = \cos(kx) + \bigg(\frac{\big(\sin(kL) + i\cos(kL)\big)*\big(\cos(kL)+i\sin(kL)\big)}{\cos^2(kL)+\sin^2(kL)} \bigg)\sin(kx) = \cos(kx) + i\frac{\sin(kx)}{\cos^2(kL)+\sin^2(kL)} = \cos(kx) + i \sin(kx) = \e^{ikx} $
A ce stade, on se rend compte que l'on aurait dû résoudre l'équation avec la forme de solution $ A\e^{ikx} + B \e^{-ikx} $.

On a donc $ |\e^{ikx}|=1 $ et $ \Re(\e^{ikx})=\cos(kx) $

Donc $ h(x)=\frac{\Re(\phi)}{|\phi|} = \cos(kx) $

Avec le temps : $ h(x)=\cos(kx - \omega t) $

Ce qui donne :

Résolution par la méthode d'homotopie

Etablissons d'abord la relation homotopique :
$ (1-p)\phi_{xx} + p*(\phi_{xx}+k^2\phi) = 0 $

D'où :
$ \phi_{xx} + pk^2\phi = 0 $
$ \Leftrightarrow\sum_{i=0}^N p^i*\phi_{ixx} +pk^2*\sum_{i=0}^N p^i*\phi_{i} = 0 $
$ \Leftrightarrow\sum_{i=0}^N p^i*\phi_{ixx} +k^2*\sum_{i=0}^N p^(i+1)*\phi_{i} = 0 $
$ \Leftrightarrow\phi_{0,xx} +k^2*\sum_{i=0}^N p^(i+1)*\phi_{i} = 0 $

on réalise le changement de variable suivant i= i+1. D'où
$ \Leftrightarrow\phi_{0,xx} +k^2*\sum_{i=1}^N p^j*\phi_{i-1} = 0 $
$ \Leftrightarrow\phi_{0,xx} +k^2*\sum_{i=1}^N p^j*(\phi_{i,xx}+k^2*\phi_{i-1}) = 0 $

On obtient alors l'équation suivante: $ \phi_{i,xx}+k^2\phi_{i-1} = 0 $. Pour $ j \in [\![1;n]\!] $, on a alors:
$ \phi_{j,x} = -\int k^2*\phi_{j-1}*dx + A $
$ \phi_{j}= -\int\int k^2*\phi_{j-1}dx^2 + Ax + B $

On dit que $ \phi(x=0) = 0 \Rightarrow B = 0 $.
Déterminons maintenant A. Nous avons $ \phi_{x = L} = ik\phi(L) $ :

$ \Leftrightarrow \int (k^2*\phi\_{j-1}dx)(L) + A = ik\phi_{i} (L) $
$ \Leftrightarrow \int (k^2*\phi\_{j-1}dx)(L) + A = ik(\int \int k^2*\phi_{j-1} dx^2)(L) + ikAL $
$ \Leftrightarrow A*(1 - ikL) = ikk(\int \int k^2*\phi_{j-1} dx^2)(L)-(\int k^2 \phi_{j-1} dx)(L) $
$ \Leftrightarrow A = \frac{ik(\int \int k^2*\phi_{j-1} dx^2)(L) - (\int k^2 \phi_{j-1}dx)(L)}{1 - ikL} $

En conclusion , $ \phi_{j} = -k^2* \int\int \phi_{j-1}dx^2 + \frac{ik(\int\int k^2*\phi_{j-1} dx^2)(L) - (\int k^2 \phi_{j-1}dx)(L)}{1 - ikL} * x $

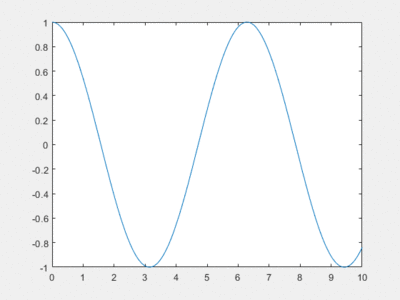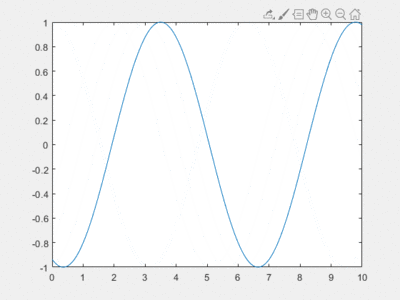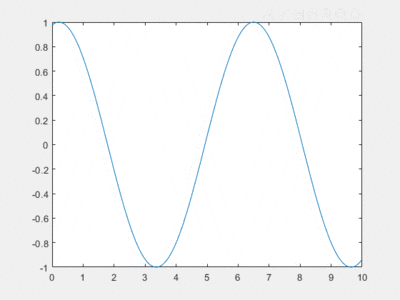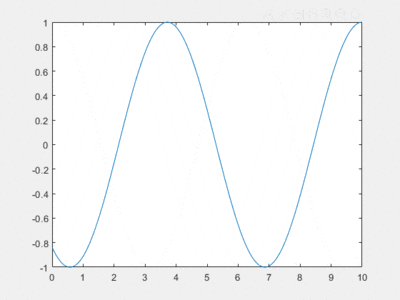
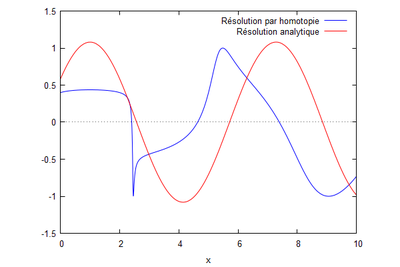
Après codage de la fonction sur Maxima on obtient la courbe suivante pour N=15 :

Cas n°2 : Domaine unidimensionnel avec fond plat de longueur L : avec onde réfléchie

Résolution analytique

Dans ce second cas, on se place en domaine unidimensionnel avec un fond plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_x=ik(2−\phi) $ et une réflexion totale en amont $ \phi_x=0 $.

On en déduit les conditions aux limites suivantes:

En Aval pour $ x=0 $ : $ \phi_x=ik(2−\phi) $
En Amont pour $ x=L $: $ \phi_x=0 $

On va reprendre l'équation de Berkhoff simplifiée (la même que celle utilisée dans le cas 1). Le problème simplifié revient à résoudre l'équation différentielle homogène suivante (EDH) : $ \phi_{xx} + k^2\phi=0 $

L'équation caractéristique associée à (EDH) est $ r^2+k^2=0 \Longleftrightarrow r=\pm ik $

La solution obtenue est $ \phi(x)=A\e^{-ikx} + B \e^{ikx} $

Déterminons A et B d'après les conditions aux limites:

pour $ x= 0 $ : $ \phi_{x} = ik(2-\phi) $
pour $ x=L $ : $ \phi_{x}= 0 $

On obtient alors $ B=1 $ et $ A = \e^{2ikL} $

La solution obtenue est : $ \phi(x)=\e^{2ikL} \e^{-ikx} + \e^{ikx} $

c'est à dire $ \phi(x)=e^{ik({2L-x})} + \e^{ikx} $

En prenant la partie réelle de $ \phi $ :
$ \Re (\phi) = \cos(k(2L-x))+\cos(kx)) $
Avec le temps :
$ h(x)=\cos(k(2L-x)-\omega t)+\cos(kx - \omega t)) $

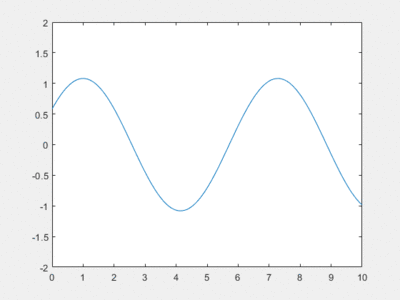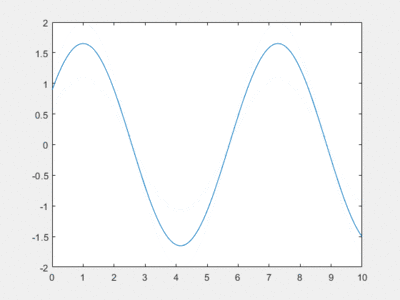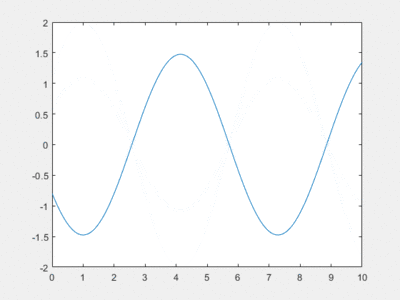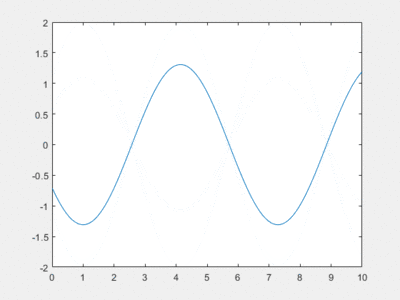
Résolution par homotopie

De même que dans le cas n°1, on a l'équation d'homotopie pour $ i>1 $ : $ \phi_{i,xx}+k^2 \phi_{i-1} = 0 $

On trouve de la même manière que dans le cas précédent $ A = (\int \int \phi_{i-1} dx^2)(L) $ et $ B=2-\frac{A}{i k} $.

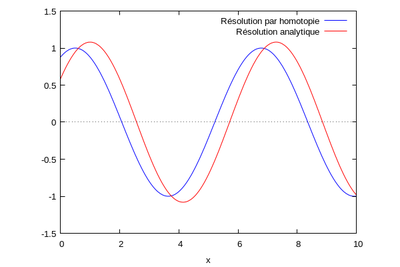
Cela nous donne le graphique suivant, pour N=70 :

L'erreur entraînant un graphique comme celui-ci est inconnue...

Cependant on peut résoudre le problème par homotopie par image virtuelle.
Il suffit de superposer une onde évoluant dans le sens des x croissants, et une onde évoluant dans le sens des x décroissants, toutes deux de même période.

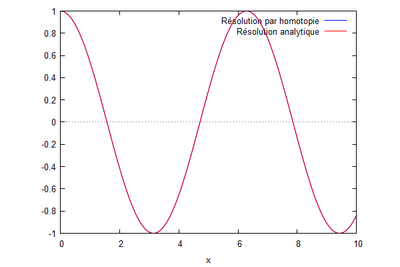
Cela donne le graphique suivant :

La hauteur de houle obtenue par homotopie semble très proche de celle qui est obtenue par solution analytique. La phase également, mais comporte une importance beaucoup moins grande dans le projet de modélisation.

Cas n°3 : Domaine unidimensionnel avec fond de pente constante : sans onde réfléchie

Résolution analytique

Dans le cas où k est constant , on obtient grâce à l'équation de Berkoff , l'équation suivante : $ (H0 - Px )*\phi_{xx} - P*\phi_{x} + k^2 *(H0 - Px)*\phi(x) = 0 $

En réalisant le changement de variable $ X = \frac{k*(H0 -Px)}{P} $, on obtient une équation de Bessel de la forme : $ X^2*\phi_{xx} + X *\phi_{x} + X^2*\phi(x) = 0 $

D'où la solution générale : $ \phi(x) = A*J0(X)+B*Y0(X) $

En posant $ x_L=\frac{k}{\alpha}(\alpha L-H_0) $ et $ x_0=-\frac{k}{\alpha}H_0 $

A l'aide des conditions limites en aval $ \phi(0) = 1 $ et en amont $ \phi_{x} = ik\phi $, on obtient la formule générale de $ \phi $ qui est :
$ _\phi(x) = \frac{J0(x)*(Y1(xL)-iY0(xL)) + Y0(x)*(J1(xL)+iJo(xL))}{J0(x0)*(Y1(xL)-iY0(xL))+Y0(x0)*(J1(xL)+iJ0(xL))} $

Résolution par homotopie

1er essai :

Pour écrire la relation d'homotopie, on va choisir comme opérateur linéaire :
$ L(U) = \frac{d^2}{dx^2} $
et non linéaire :$ N(U) = \frac{e}{1+ex} \frac{d}{dx}(U) + k^2 U $
En ayant posé que $ e = -\frac{P}{H_0} $

On obtient donc l'équation d'homotopie suivante :

$ (1-p)\phi_{xx} + p(\phi_{xx} + \frac{e}{1+ex} \phi_{x} +k^2 \phi)=0 $
Ce qui nous donne comme kième équation (avec k différent de 1) :

$ \phi_{i,xx}+\frac{e}{1+ex} \phi_{i-1,x}+k^2 \phi = 0 $ => Le programme n'aboutit pas

2ème essai :

Avec l'équation d'homotopie suivante :
$ \Phi_{xx} +p(ex\Phi_{xx}+e\Phi_{x}+k^{2}(1+ex)\Phi)=0 $

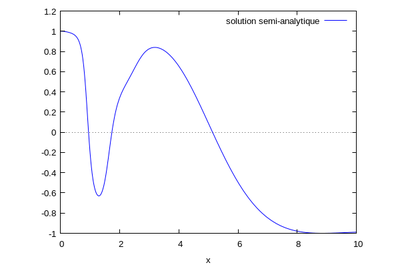
On a une courbe telle que, avec $ e=-\frac{1}{10} $ et $ N=50 $ :

La courbe analytique ne s'affiche pas, on ne peut donc vérfier si la courbe est cohérente.

Cas n°5: Domaine bidimensionnel avec fond plat : sans onde réfléchie

Dans ce cas on se place en domaine bidimensionnel avec les même conditions que dans le cas n°1.

L'équation de berkhoff s'écrit donc en domaine bidimensionnel : $ \nabla (gH\nabla\phi)+k^2gH\phi=0 $

on a $ C=C_g=\sqrt{gH} $, finalement comme H est constant l'équation s'écrit finalement :

$ \nabla (\nabla\phi)+k^2\phi=0 \Longleftrightarrow \Delta \phi +k^2 \phi=0 $

On ne peut pas résoudre cette équation analytiquement on choisit de résoudre cette équation par une méthode semi-analytique c'est à dire par la méthode de l'homotopie.

En supposant que $ \phi $ ne dépend pas de y :

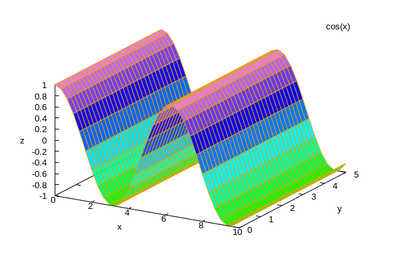
On essaye plusieurs pistes :

Piste 1 : utilisation de théorèmes connus pour simplifier le calcul

On a l'équation suivante :

$ \Delta \phi_{i} = -k^2 \phi_{i-1} $

$ \Longrightarrow div (grad (\phi_i))= -k^2 \phi_{i-1} $

$ \Longrightarrow \int \int \int div(grad(\phi_i)) d \tau = - \int \int \int k^2 \phi_{i-1} d \tau $

Par le théorème de Stokes pour tout volume et pour toute surface fermée délimitant ce volume :

$ \Longrightarrow \int \int grad(\phi_i) dS = - \int \int \int k^2 \phi_{i-1} d \tau $

Par intégration selon $ z $ :

$ \Longrightarrow \int \int \int grad(\phi_i)) d \tau = - \int \int \int \int k^2 \phi_{i-1} d \tau dz $

Par le théorème du gradient pour tout volume et pour toute surface fermée délimitant ce volume :

$ \Longrightarrow \int \int \phi_i dS = - \int \int \int \int k^2 \phi_{i-1} dS dz^2 $

$ \Longrightarrow \int \int \phi_i dx dy = - \int \int dz^2 * \int \int k^2 \phi_{i-1} dx dy $

En supposant que la hauteur de la houle au dessus ou au dessous de la profondeur moyenne est négligeable devant la profondeur moyenne :

$ \Longrightarrow \int \int \phi_i dx dy = - \frac{H^2}{2} \int \int \phi_{i-1} dx dy $

Est-ce utile ? Est-ce que ça a un intérêt ? => Surement pas...

Piste 2 : passage en polaire

On considère un domaine en quart de cercle de rayon L où on impose $ \phi=1 $ en $ r=0 $ et $ \phi_{x}(L)=ik\phi(L) $ en $ r=L $.
On a donc le laplacien en coordonnées cylindriques qui s'exprime tel que :

$ \Delta \phi = \frac{1}{r}(\frac{\partial}{\partial r}(r \frac{\partial}{\partial r} \phi)) $
en supposant que $ \phi $ ne dépend pas de $ \theta $ et de $ z $.

On obtient donc que pour la relation d'homotopie on a :

$ \phi_i=\int \frac{-\int k^2 \phi_{i-1}(r)rdr}{r}dr $

On a donc $ A=\frac{ik((\int \frac{-\int k^2 \phi_{i-1}(r)rdr}{r}dr)(L))-(\frac{1}{r}\int -k^2 \phi_{i-1}(r)rdr)(L)}{1-ikL} $

On a des problèmes d'affichages, à venir plus tard.

Piste 3 : on essaye de changer la relation d'homotopie

On veut ici tenter de changer la relation d'homotopie de celle habituellement proposée, puisque le laplacien n'est pas un opérateur linéaire.
Prenons :

$ L(\phi)=k^2 \phi $
$ N(\phi)=-(\frac{\partial^2}{\partial x^2}\phi + \frac{\partial^2}{\partial y^2}\phi) $

On a donc l'équation d'homotopie étant :

$ (1-p) k^2 \phi + p(k^2 \phi + \Delta \phi)=0 $

Ce qui donne la i-ième équation :

$ \phi_{i}=-\frac{1}{k^2}(\frac{\partial^2}{\partial x^2}\phi + \frac{\partial^2}{\partial y^2}\phi) $

Il faut donc déterminer $ \phi_0 $ pour effectuer l'homotopie.
L'équation d'ordre 0 est :

$ \Delta \phi_0 = 0 \Longleftrightarrow \frac{\partial^2}{\partial x^2}\phi_0 + \frac{\partial^2}{\partial y^2}\phi_0 = 0 $

En supposant une forme de solution telle que : $ \phi_0(x,y)=X(x)*Y(y) $, puis par séparation des variables :

$ \frac{X''(x)}{X(x)}=-\frac{Y''(x)}{Y(x)}=-\lambda^2 $

et en omettant le cas trivial lorsque $ \lambda > 0 $, on a que lorsque $ \lambda < 0 $, la solution devient :

$ X(x)=A \sin(\lambda x) + B \cos(\lambda x) $
$ Y(y)=C \sinh(\lambda y) + D \cosh(\lambda y) $

Donc on a :

$ \phi_0 = (A \sin(\lambda x) + B \cos(\lambda x))(C \sinh(\lambda y) + D \cosh(\lambda y)) $

Il faudrait maintenant chercher A, B, C et D, puis réaliser le programme d'homotopie. => A voir si c'est la bonne méthode.

Bon courage et n'hésitez pas à communiquer avec moi par mail: jm.tanguy@shf-hydro.org