Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/trinome2: BUCHER-GIORGI-LOTHON : Différence entre versions
(→Résolution par la méthode homotopique) |
|||
| Ligne 158 : | Ligne 158 : | ||
avec une évolution dans le temps : <math>\color{blue}h(x,t)=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}}*\cos(wt)</math> | avec une évolution dans le temps : <math>\color{blue}h(x,t)=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}}*\cos(wt)</math> | ||
| + | |||
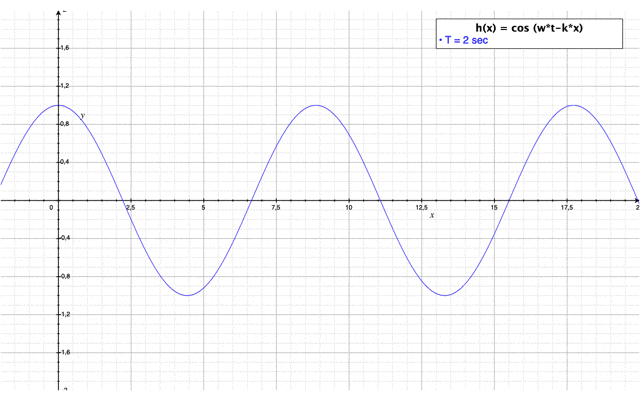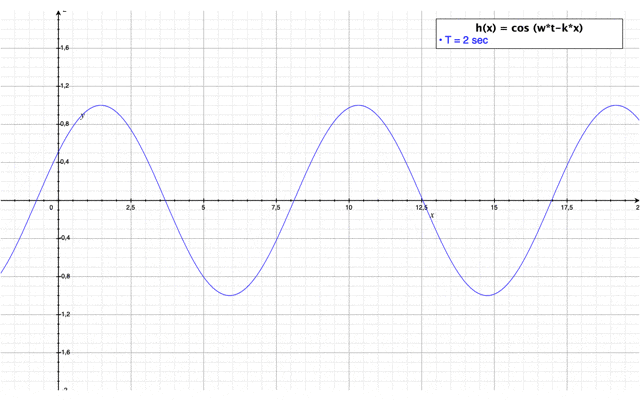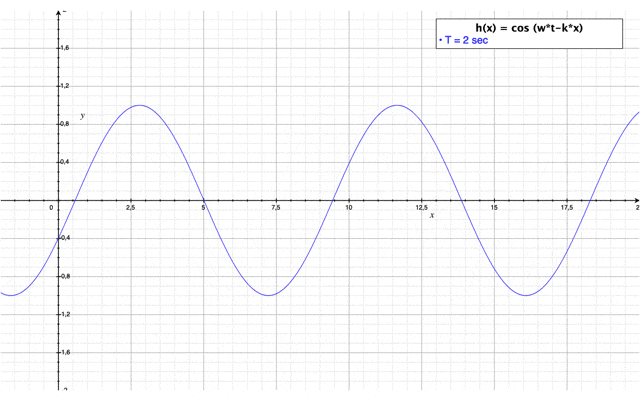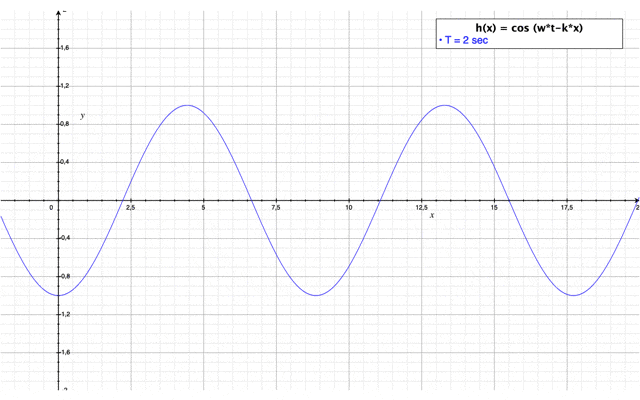
| + | [[Fichier:Cas_2.PNG|center|550px|Représentation graphique de la hauteur de houle du cas n°2]] | ||
==== Résolution par la méthode homotopique==== | ==== Résolution par la méthode homotopique==== | ||
Version du 12 juin 2020 à 16:03
Contextualisation
Le thème d’étude est la quantification de l’impact des houles sur le littoral. La probabilité de survenue d’événements extrêmes va considérablement augmenter à cause du changement climatique et leurs impacts sur le littoral va provoquer des désordres sur les secteurs les plus vulnérables entraînant le recul du trait de côte, la disparition de propriétés et d’ouvrages et des déplacements de populations.
Modèle de Berkhoff
Dans le but de modéliser la houle, nous allons utiliser le modèle de Berkhoff. Ce modèle est utilisé pour prédire la propagation et l'impact des vagues sur les côtes. C'est un modèle bi-dimensionnel qui a pour expression:
$ \frac{\partial }{\partial x_i}(CC_g \frac{\partial \phi}{\partial x_i})+ k^2CC_g\phi = 0 $ avec $ i = {1,2} $
On note:
$ \phi $ : le potentiel de vitesse
$ C $ : la célérité de l'onde
$ C_g $ : la célérité de groupe des vagues
$ k $ : le nombre d'onde
$ H $ : la hauteur de la houle
Il se base sur un grand nombre d'hypothèses:
- le fluide est considéré conne étant parfait, incompressible et irrotationnel
- le fond est fixe et imperméable
- la hauteur de la houle est faible par rapport à sa longueur d’onde et à la profondeur
- les sollicitations atmosphériques à la surface libre sont négligées
Nous nous plaçons dans le cadre des ondes longues, ce qui signifie que $ C = C_g = \sqrt{gH} $.
L'équation devient alors:
$ \frac{\partial }{\partial x_i}(H \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 $
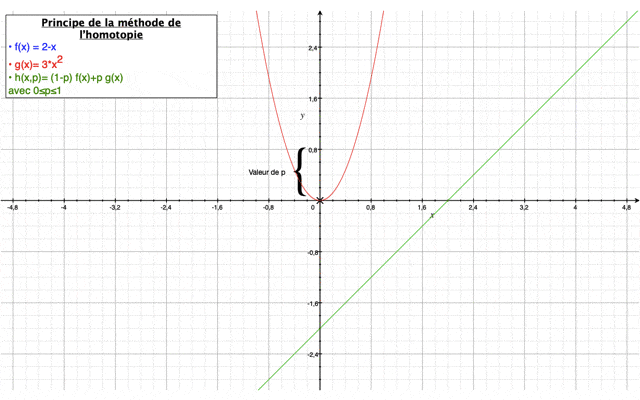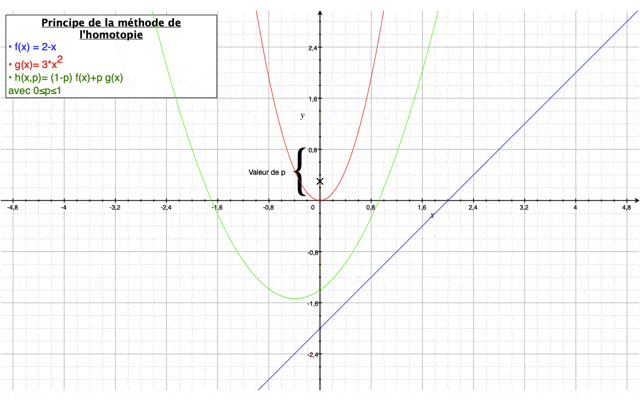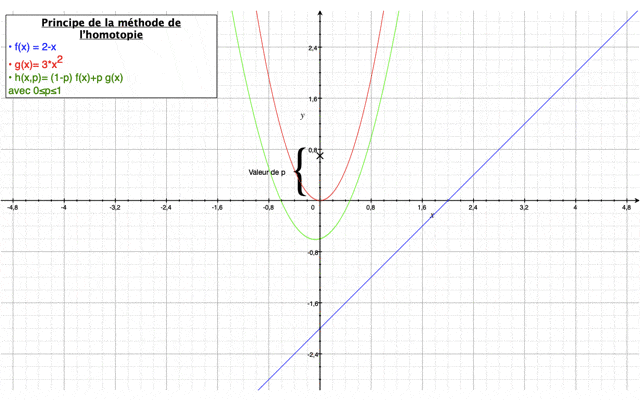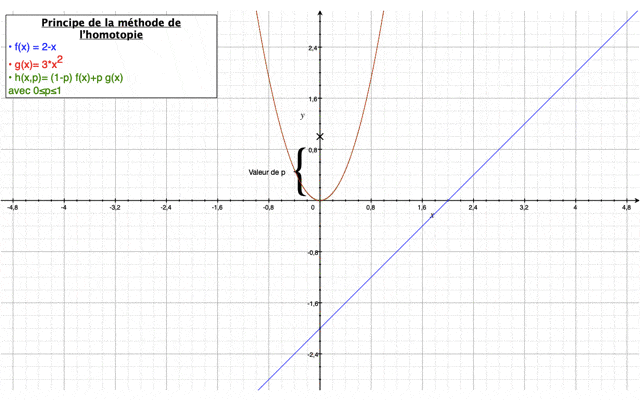
Méthode homotopique
Tout d'abord, la méthode de l'homotopie a pour but de résoudre des équations différentielles et des intégrales. Elle permet à partir d’une solution connue relativement simple de converger vers une solution complète grâce à un paramètre p qui varie entre 0 et 1 et qui assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre.
Elle est définie comme suit :$ (1−p)[L(U(x,t);p)−L(u0(x,t))]+cH(p)[L(U(x,t);p)−N(U(x,t),p)−f(x)] $
avec L est un opérateur linéaire, N un opérateur non-linéaire, f les termes complémentaires de l’équation et u0 est une estimation initiale de la solution.
Dans notre cas, on prendra $ H(p)=p $
Ci-dessous est présentée dans une vidéo le principe général de la méthode.
Étude cas
Cas n°1 : canal uniforme unidimensionnel plat de longueur L avec sortie libre amont
Résolution : Méthode analytique
Dans le cadre de l'hypothèse canal uniforme plat, on a $ H = constante $. On a alors:
$ \frac{\partial }{\partial x_i}(H \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 \Leftrightarrow H\frac{\partial }{\partial x_i}( \frac{\partial \phi}{\partial x_i})+ k^2H\phi = 0 \Leftrightarrow \cancel{H}\frac{\partial }{\partial x_i}( \frac{\partial \phi}{\partial x_i})+ k^2\cancel{H}\phi = 0 \Leftrightarrow \frac{\partial^2 \phi}{\partial x_i^2}+ k^2\phi = 0 $
On obtient alors une équation différentielle du second degré sans second membre à résoudre. L'équation d’onde est la suivante: $ h(x,t)=a_0\cos(kx-\omega t) $
$ \phi(x)=A\cos(kx)+B\sin(kx) $
avec $ k = \frac{\omega}{c} \Rightarrow k = \frac{2\pi}{T\sqrt{gH_0}} $
D'après les conditions initiales, on a:
$ \bullet \phi(0)=1 \Rightarrow A=1 $
$ \bullet \phi(L)=ik\phi \Rightarrow B= i $
On en déduit l'expression de $ \phi $:
$ \phi(x)= \cos(kx)+i\sin(kx) $
La hauteur de houle est :
$ H = \frac{Re(\phi)}{ |\phi|}= \cos(kx) $
avec une évolution dans le temps : $ \color{blue}h(x,t)=\cos(wt-kx) $
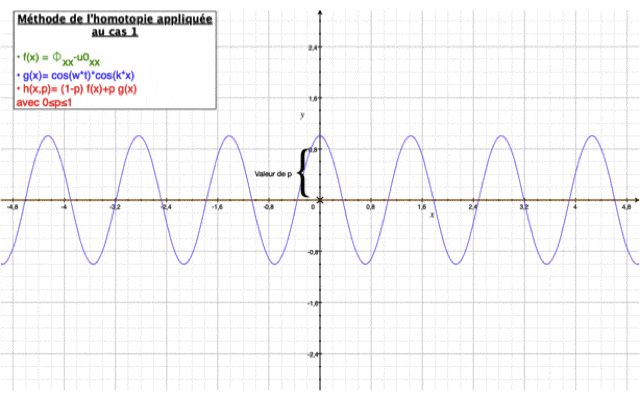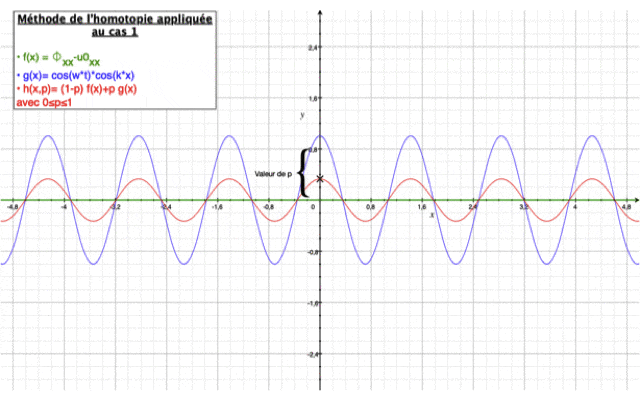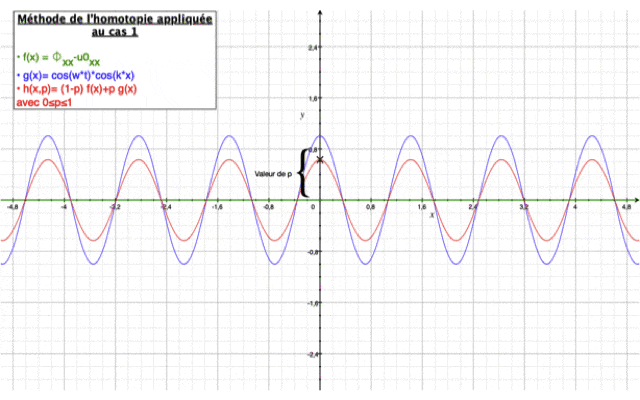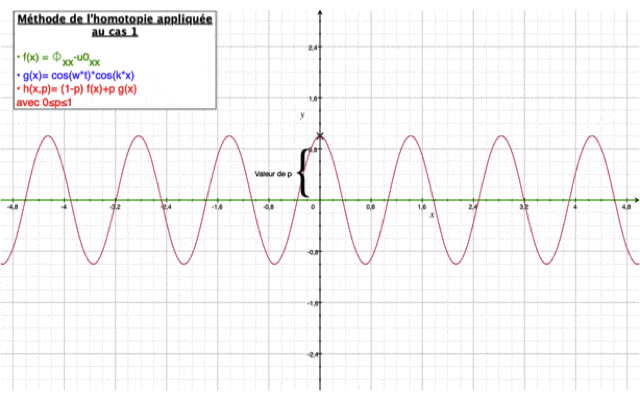
Résolution par la méthode homotopique
L'équation de l'homotopie est de la forme : $ (1-p)[\phi_{xx}-u0_{xx}]+p[\phi_{xx}+k_0^2\phi]=0 $
$ \phi=\sum_{k=0}^\infty p^n \phi_n $
$ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $
Ordre 0 : $ \phi_{0,xx}-u0{xx}=0 $
Ordre 1 :$ \phi_{1,xx}+u0{xx}+k_0^2 \phi_0=0 $
Ordre 2 : $ \phi_{2,xx}+k_0^2 \phi_1=0 $
Ordre 3 : $ \phi_{3,xx}+k_0^2 \phi_2=0 $ .
.
.
.
Ordre N : $ \phi_{N,xx}+k_0^2 \phi_{N-1}=0 $
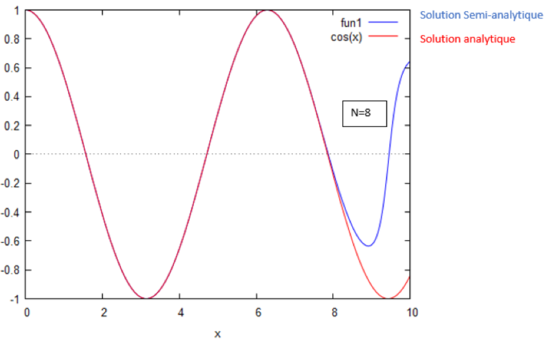
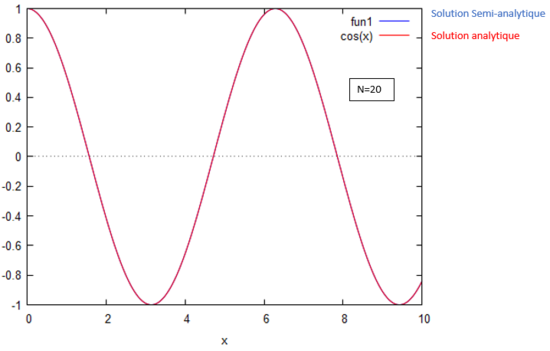
Ci-dessous cette vidéo illustre le principe de la méthode appliquée au Cas n°1
Représentation animée du modèle
Valeurs attribuées pour le régime de houle :
$ H_0=2 m $
$ T=2 s $
$ c=4.43 m.s^{-1} $
$ k=0.709 m^{-1} $
Cas n°2 : canal uniforme unidimensionnel réflexion totale amont
Résolution : Méthode analytique
L'équation différentielle est la même que dans le cas n°1. Seules les conditions initiales changent.
$ \phi(x)=Ae^{-ikx}+Be^{ikx} $
avec $ k = \frac{\omega}{c} \Rightarrow k = \frac{2\pi}{T\sqrt{gH_0}} $
D'après les conditions initiales, on a:
$ \bullet $ En aval: $ \phi_x=ik(2-\phi) \Rightarrow B=1 $
$ \bullet $En amont: $ \phi_x=0 \Rightarrow A = e^{2ikL} $
On en déduit l'expression de $ \phi $:
$ \phi(x)= e^{ik(2L-x)}+e^{ikx} = \cos(2kl-kx)+i\sin(2kL-kx)+\cos(kx)+i\sin(kx) $
La hauteur de la houle est :
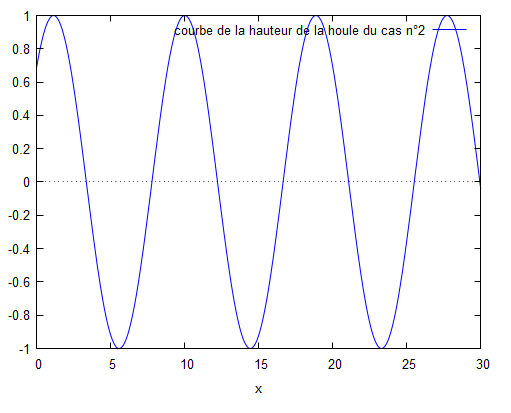
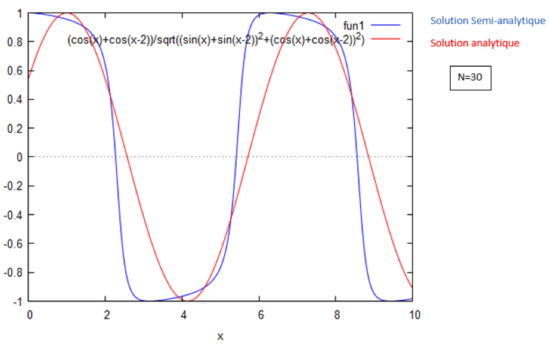
$ H =\frac{Re(\phi)}{|\phi|}=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}} $
avec une évolution dans le temps : $ \color{blue}h(x,t)=\frac{\cos(2kL-kx)+cos(kx)}{\sqrt{\Big(\cos(2kL-kx)+cos(kx)\Bigr)^2+\Big(\sin(2kL-kx)+\sin(kx)\Bigr)^2}}*\cos(wt) $
Résolution par la méthode homotopique
L'équation de l'homotopie est la même que pour le cas n°1, seules les conditions initiales changent.
Cas n°3 : Domaine monodimensionnel de longueur L avec pente du fond constante
Résolution : Méthode Analytique
Berkhoff :
$ \frac{\partial}{\partial x}(H\frac{\partial\phi}{\partial x})+k^2H\phi=0 $ Expression de la hauteur
$ H(x)=H_0-sx $ avec s la pente du fond du bassin
$ k=k_0 $
On obtient :
$ (H_0-sx)\frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k_0^2(H_0-sx)\phi(x) $
En réalisant le changement de variable suivant :$ X=H_0-sx $
On obtient l'équation : $ s^2X\frac{\partial^2\phi}{\partial X^2}+s^2X\frac{\partial\phi}{\partial X}+k_0^2X\phi(X)=0 $
En divisant par $ s^2 $ puis en multipliant par $ X $
On obtient l'équation de Bessel suivante :
$ X^2\frac{\partial^2\phi}{\partial X^2}+X\frac{\partial\phi}{\partial X}+\Big(\frac{k_0}{s}\Bigr)^2X^2\phi(X)=0 $
La solution est de la forme :
$ \phi(X)=AJ_0(X)+BY_0(X) $ avec $ J_0(X)=\sqrt{\frac{2}{\pi X}}\cos(X-\frac{\pi}{4}) $ et $ Y_0(X)=\sqrt{\frac{2}{\pi X}}\sin(X-\frac{\pi}{4}) $
c'est à dire : $ J_0(x)=\sqrt{\frac{2}{\pi (H_0-sx)}}\cos(H_0-sx-\frac{\pi}{4}) $ et $ Y_0(x)=\sqrt{\frac{2}{\pi(H_0-sx)}}\sin(H_0-sx-\frac{\pi}{4}) $
Avec les conditions initiales, on exprime les constantes A et B :
$ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $
Expression de la hauteur :
$ H= \frac{Re(\phi)}{|\phi|} $
Résolution par la méthode homotopique
L'équation de l'homotopie est :
$ (1-p)[\phi_{xx}-u0_{xx}]+p[(1-mx)\phi_{xx}-m\phi_x+k_0^2(1-mx)\phi]=0 $ avec $ m=\frac{s}{H_0} $
$ \phi=\sum_{k=0}^\infty p^n \phi_n $
$ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $
$ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $
Ordre 0 : $ \phi_{0,xx}-u0{xx}=0 $
Ordre 1 : $ \phi_{1,xx}+u0{xx}-mx\phi_{0,xx}-m\phi_{0,x}+k_0^2(1-mx)\phi_0=0 $
Ordre 2 : $ \phi_{2,xx}-mx\phi_{1,xx}-m\phi_{1,x}+k_0^2(1-mx)\phi_1=0 $ .
.
.
.
Ordre N : $ \phi_{N,xx}-mx\phi_{N-1,xx}-m\phi_{N-1,x}+k_0^2(1-mx)\phi_{N-1}=0 $
Représentation animée du modèle
Cas n°4 : Domaine monodimensionnel de longueur L avec pente du fond exponentielle et sortie libre amont
Résolution : Méthode analytique
Expression de la hauteur
$ H(x)=H_0\mathrm{e}^{-sx} $
L'équation de Berkhoff devient : $ H_0\mathrm{e}^{-sx}\frac{\partial^2\phi}{\partial x^2}-sH_0\mathrm{e}^{-sx}\frac{\partial\phi}{\partial x}+k_0^2H_0\mathrm{e}^{-sx}\phi=0 $
$ H_0\mathrm{e}^{-sx}\Big(\frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k_0^2\phi\Bigr)=0 $
$ H_0\mathrm{e}^{-sx}\neq0 $
Donc on obtient l'équation suivante : $ \frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k_0^2\phi=0 $
L'équation caractéristique associée est de la forme :$ x^2-sx+k_0^2=0 $
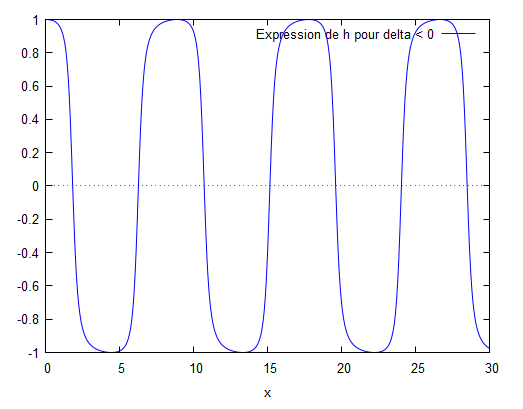
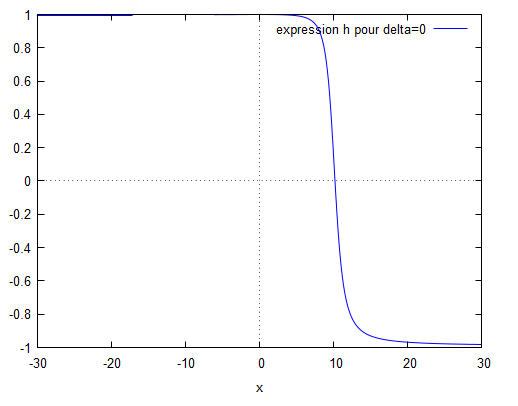
La forme des solutions dépend du signe de $ \Delta $: $ \Delta=s^2-4k_0^2 $
$ \bullet \Delta<0 $; l'équation est de la forme :$ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[c_1\cos\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)+c_2\sin\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)] $
$ \bullet \Delta=0 $; l'équation est de la forme : $ \phi(x)=(c_1x+c_2)\mathrm{e}^{\frac{s}{2}x} $
$ \bullet\Delta>0 $ ; l'équation est de la forme : $ \phi(x)=c_1\mathrm{e}^{\frac{s-\sqrt{s^2-4k_0^2}}{2}x}+c_2\mathrm{e}^{\frac{s+\sqrt{s^2-4k_0^2}}{2}x} $
Avec les conditions initiales, on exprime les constantes $ c_1 $ et $ c_2 $ :
$ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $
$ \bullet \Delta<0 $ : on note $ u=\frac{s}{2} $ et $ v=\frac{\sqrt{s^2-4k_0^2}}{2} $
$ c_1=1 $ et $ c_2=\frac{v\sin(vL)+\cos(vL)(ik-1)}{v\cos(vL)+\sin(vL)(1-ik)} $
L'équation s'écrit : $ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[\cos\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)+\frac{v\sin(vL)+\cos(vL)(ik-1)}{v\cos(vL)+\sin(vL)(1-ik)}\sin\Big(\frac{\sqrt{s^2-4k_0^2}}{2}x\Bigr)] $
Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $
$ \bullet \Delta=0 $ :
$ c_1=\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL} $ et $ c_2=1 $
L'équation s'écrit : $ \phi(x)=(\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL}x+1)\mathrm{e}^{\frac{s}{2}x} $
Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $
$ \bullet\Delta>0 $ : on note $ x_1=\frac{s-\sqrt{s^2-4k_0^2}}{2} $ et $ x_2=\frac{s+\sqrt{s^2-4k_0^2}}{2} $
$ c_1=\frac{1}{\mathrm{e}^{L(x_1-x_2)}\frac{x_1-ik}{ik-x_2}+1} $ et $ c_2=\frac{1}{1+\mathrm{e}^{L(x_2-x_1)}\frac{ik-x_2}{x_1-ik}} $
L'équation s'écrit : $ \phi(x)=\frac{1}{\mathrm{e}^{L(x_1-x_2)}\frac{x_1-ik}{ik-x_2}+1}\mathrm{e}^{\frac{s-\sqrt{s^2-4k_0^2}}{2}x}+\frac{1}{1+\mathrm{e}^{L(x_2-x_1)}\frac{ik-x_2}{x_1-ik}}\mathrm{e}^{\frac{s+\sqrt{s^2-4k_0^2}}{2}x} $
Expression de la hauteur :
$ H= \frac{Re(\phi)}{|\phi|} $
Résolution par la méthode homotopique
L'équation de l'homotopie est : $ (1-p)[\phi_{xx}-u0_{xx}]+p[\phi_{xx}-s\phi_x+k_0^2\phi]=0 $
$ \phi=\sum_{k=0}^\infty p^n \phi_n $
$ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $
$ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $
Ordre 0 : $ \phi_{0,xx}-u0_{xx}=0 $
Ordre 1 : $ \phi_{1,xx}+u0_{xx}-s\phi_{0,x}+k_0^2\phi_0=0 $
Ordre 2 : $ \phi_{2,xx}-s\phi_{1,x}+k_0^2\phi_1=0 $
.
.
.
Ordre N : $ \phi_{N,xx}-s\phi_{N-1,x}+k_0^2\phi_{N-1}=0 $
 S'abonner à un flux RSS
S'abonner à un flux RSS