Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/BRETON-NGUYEN-SALLES : Différence entre versions
(→Solution analytique) |
|||
| Ligne 170 : | Ligne 170 : | ||
En multipliant par X et en divisant par pK, on a <math>X^2\phi_{XX}+X\phi_X+X^2\phi=0 </math> <br> | En multipliant par X et en divisant par pK, on a <math>X^2\phi_{XX}+X\phi_X+X^2\phi=0 </math> <br> | ||
| − | On a donc la solution générale <math>\phi(x)=A.J_0(x)+B.Y_0(x) </math> avec <math>J_0</math> une fonction de Bessel de 1ère espèce et <math>Y_0</math> une fonction de Bessel de 2ème espèce. | + | On a donc la solution générale <math>\phi(x)=A.J_0(x)+B.Y_0(x) </math> avec <math>J_0</math> une fonction de Bessel de 1ère espèce et <math>Y_0</math> une fonction de Bessel de 2ème espèce. |
D'après les conditions limites : <math>\phi(0)=1</math> et <math>\phi(x)=ik\phi</math> <br> | D'après les conditions limites : <math>\phi(0)=1</math> et <math>\phi(x)=ik\phi</math> <br> | ||
| + | |||
On trouve :<math>\phi(x) = \frac{J_0(x)*(Y_1(xL)-iY_0(xL)) + Y_0(x)*(J_1(xL)+iJ_0(xL))}{J_0(x_0)*(Y_1(xL)-iY_0(xL))+Y_0(x_0)*(J_1(xL)+iJ_0(xL))} </math> | On trouve :<math>\phi(x) = \frac{J_0(x)*(Y_1(xL)-iY_0(xL)) + Y_0(x)*(J_1(xL)+iJ_0(xL))}{J_0(x_0)*(Y_1(xL)-iY_0(xL))+Y_0(x_0)*(J_1(xL)+iJ_0(xL))} </math> | ||
| + | |||
==== Solution semi-analytique (homotopie) ==== | ==== Solution semi-analytique (homotopie) ==== | ||
| Ligne 192 : | Ligne 194 : | ||
== '''Les limites du modèle''' == | == '''Les limites du modèle''' == | ||
| − | Nous rencontrons 2 grands types de limitations : les limitations physiques ainsi que les limitations mathématiques | + | Nous rencontrons 2 grands types de limitations : les limitations physiques ainsi que les limitations mathématiques |
==== Limites physiques ==== | ==== Limites physiques ==== | ||
* Le fond du canal influence la houle et réciproquement. Or, notre modèle ne prend notamment pas en compte des phénomènes tels que le transport des sédiments et des sables qui pourraient modifier le fond du canal et donc avoir une influence sur la houle. | * Le fond du canal influence la houle et réciproquement. Or, notre modèle ne prend notamment pas en compte des phénomènes tels que le transport des sédiments et des sables qui pourraient modifier le fond du canal et donc avoir une influence sur la houle. | ||
| − | * | + | * irrégularité du fond |
| − | * | + | * irrégularité u trait de côte |
* Pourquoi l'onde serait pure ??????? | * Pourquoi l'onde serait pure ??????? | ||
| − | * | + | * réalisme de certaines données (L=1m par exemple) |
| − | * | + | * la houle se différencie de la vague par son absence de relation au vent. Mais l'érosion est affectée par les 2 : vent et houle |
==== Limites mathématiques ==== | ==== Limites mathématiques ==== | ||
| − | * | + | * beaucoup de variables sont considérées constantes (<math>k,\omega,L etc</math>) |
| − | * | + | * on suppose une uniformité spatiale et temporelle du phénomène ????? |
| − | * | + | * l'ordre d'homotopie "n" influe beaucoup sur la qualité du modèle : divergence rapide si "n" petit |
Version du 20 juin 2020 à 14:50
Notre travail a pour but de modéliser l'impact du changement climatique sur les côtes, en quantifiant l'impact des houles sur le littoral.
Pour modéliser les houles, nous utilisons le modèle de Berkhoff aussi appelé équation de pente douce, obtenu en 1972. Ce modèle est une équation aux dérivées partielles, que nous nous proposons de résoudre par une méthode analytique pour les cas simples et semi-analytique pour les cas plus complexes.
Nous nous placerons dans l'hypothèse d'ondes longues et nous étudierons différents cas concrets de géométries et de conditions aux limites.
Sommaire |
Cas n°1
Cette situation traite un canal uniforme unidimensionnel plat de longueur L avec l'entrée d'une onde de fréquence unitaire $ ϕ=1 $ par l'aval et une sortie libre en amont $ ϕ_x=ikϕ $.
Dans ce cas précis, l'équation de Berkhoff se simplifie comme suit: $ \frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $
Solution analytique
Nous résolvons l'équation caractéristique associée : $ X^2 + k^2 = 0 $
$ Δ = -4k^2 $ d'où $ λ_1 = -ik $ et $ λ_2 = ik $
donc la solution est de la forme $ Ae^{-ikx}+ Be^{ikx} $, avec A et B des constantes.
Détermination des constantes A et B grâce aux conditions limites :
- $ ϕ(x=0)=1 $ → $ A+B=1 $
- $ \dfrac{\partial ϕ}{\partial x}(x=0)=-ik $ → $ A=1 $ et $ B=0 $
donc $ ϕ(x)=e^{ikx} $
$ ϕ(x,t)=e^{i(\omega t+kx)} $
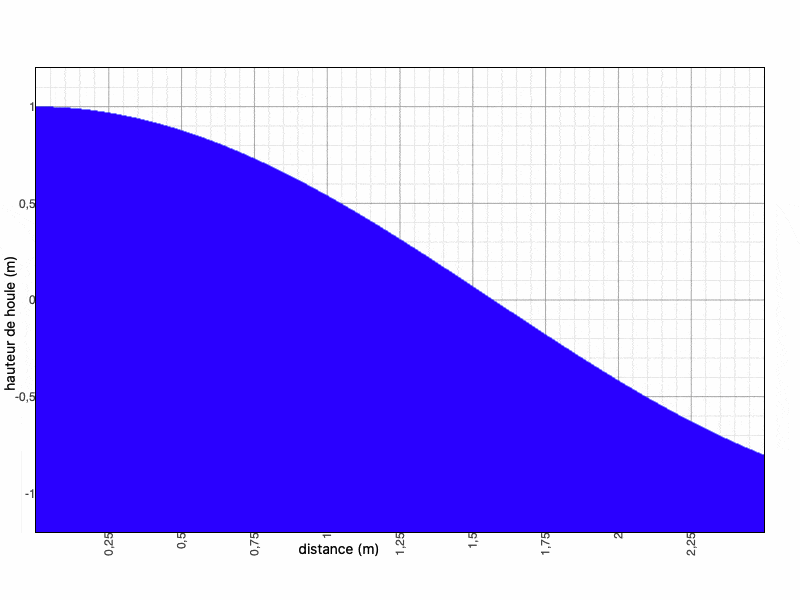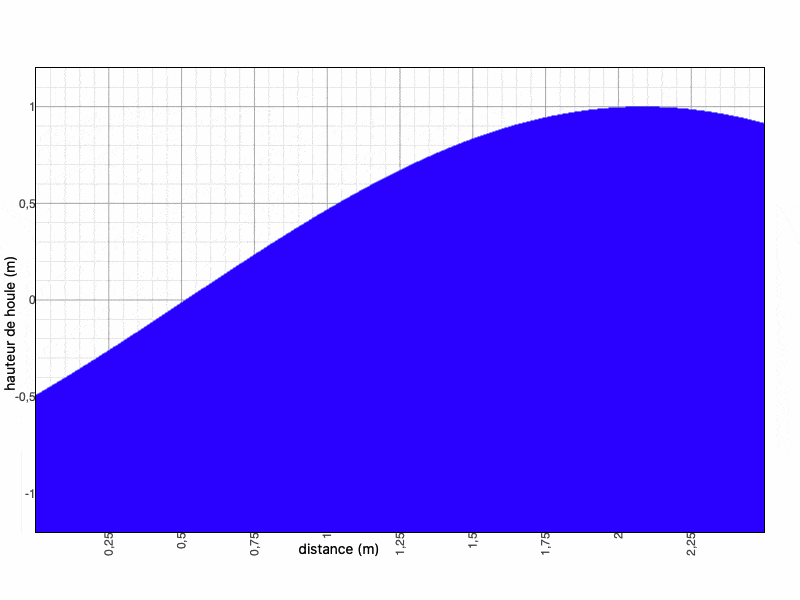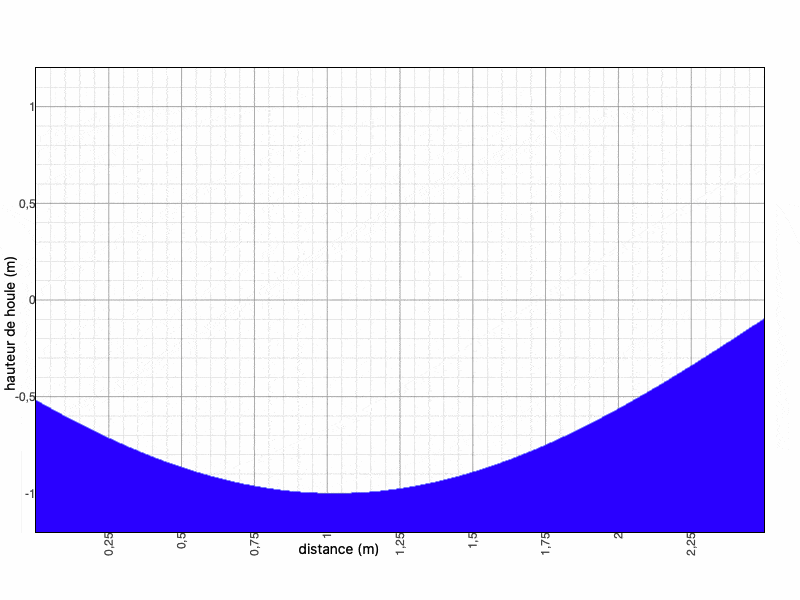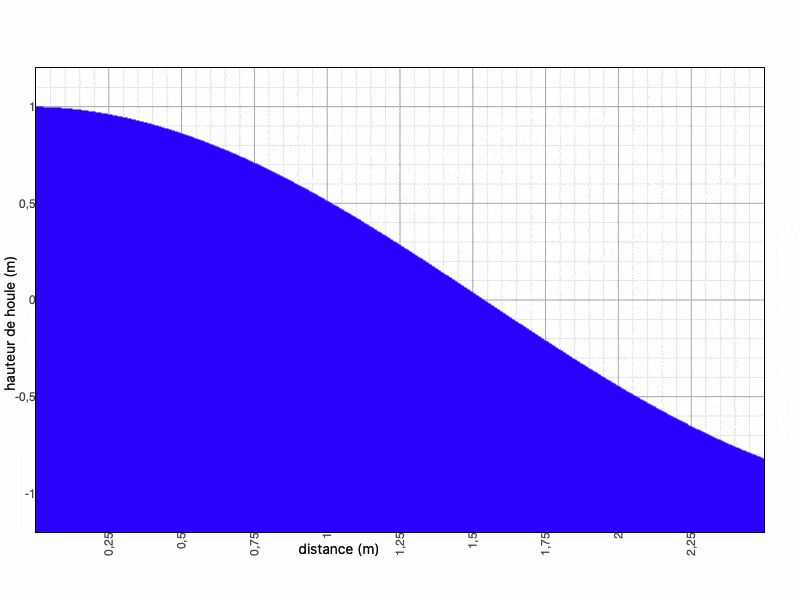
or $ H=Re(ϕ) $ donc $ \fbox{h(x,t)=cos(ωt+kx)} $
N.B. : sur les graphiques, la valeur $ h(x)=0 $ représente le niveau moyen de la surface.
Solution semi-analytique (homotopie)
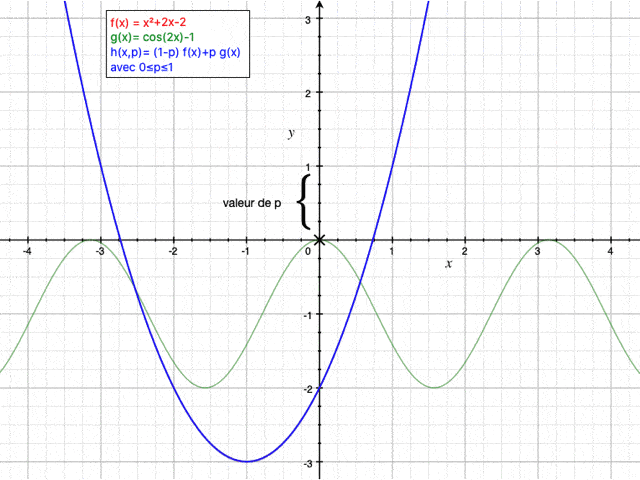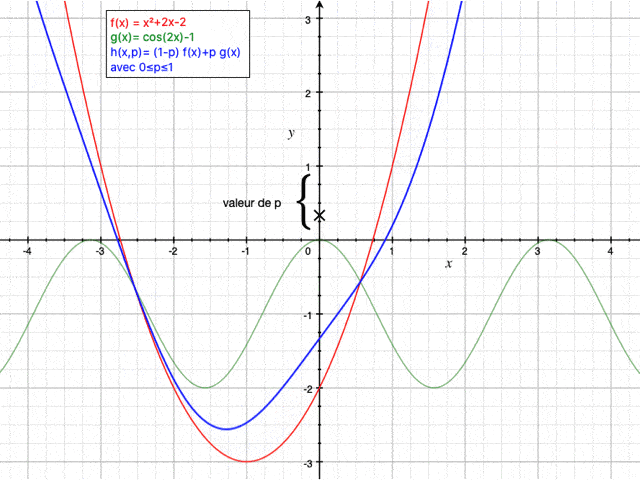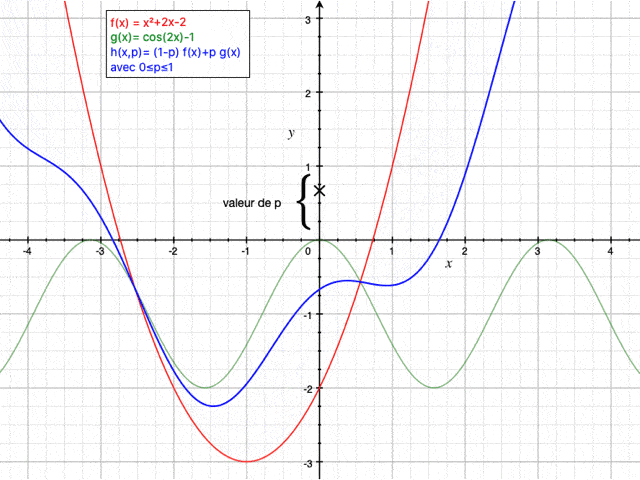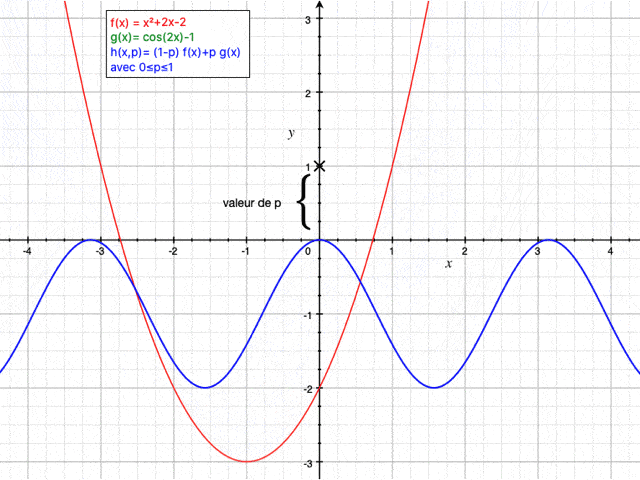
Le principe de la méthode d'homotopie est brièvement expliqué dans cette vidéo. Il s'agit de "passer" d'une fonction à une autre au travers d'un paramètre p variant de 0 à 1. Lorsque p vaut 0 et 1, $ h(x) $ est confondue avec respectivement $ f(x) $ et $ g(x) $.
Dans ce cas, la relation d'homotopie (ayant pour paramètre p entre 0 et 1) s'exprime comme ceci (on choisit la dérivée seconde comme opérateur linéaire et on part d'une solution initiale nulle):
$ (1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0 $
Or:
- $ ϕ(x,p) = \sum_{n=0}^∞ p^nϕ_n = ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $
- $ ϕ_{xx}(x,p) = ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+... $
D'où : $ (1−p)((ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...)-u_{0,xx})+p[ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)]=0 $
On développe ensuite en fonction des ordres de p.
Ordre 0 :
$ ϕ_{0,xx}-u_{0,xx}=0 $
→ $ \dfrac{\partial^2 ϕ_0}{\partial x^2} = \dfrac{\partial^2 u_0}{\partial x^2} $
→ $ \dfrac{\partial ϕ_0}{\partial x} = \dfrac{\partial u_0}{\partial x} + A $
→ $ ϕ_0(x) = Ax + u_0 + B $
Détermination des constantes A et B :
- $ ϕ(0) = 1 $ → $ 1 = u_0+B $ or $ u_0=1 $ donc $ B=0 $
- $ \dfrac{\partial ϕ}{\partial x} = ikϕ $ or $ ϕ = Ax + B + u_0 $ et $ \dfrac{\partial ϕ}{\partial x} = A $
d'où pour $ x=L $, $ A = ik(AL+B+u_0) $ ↔ $ A = \dfrac{ik}{1-ikL} $
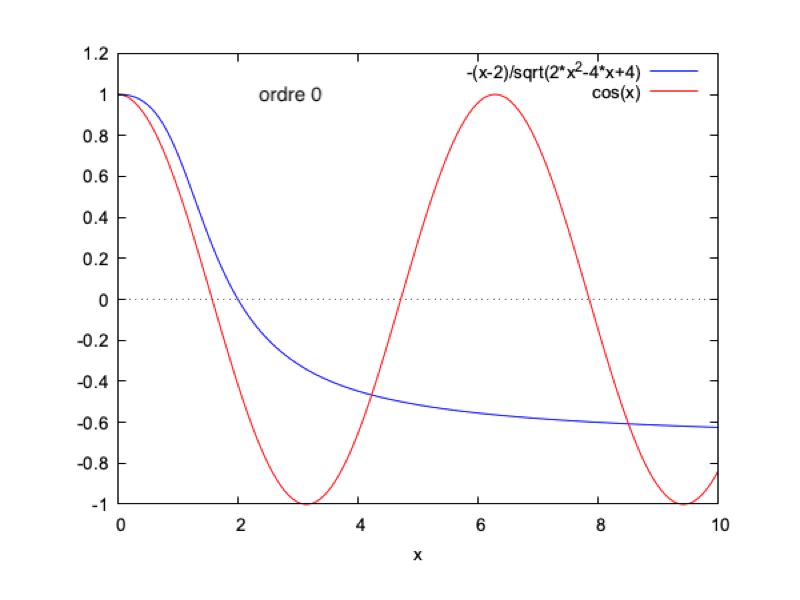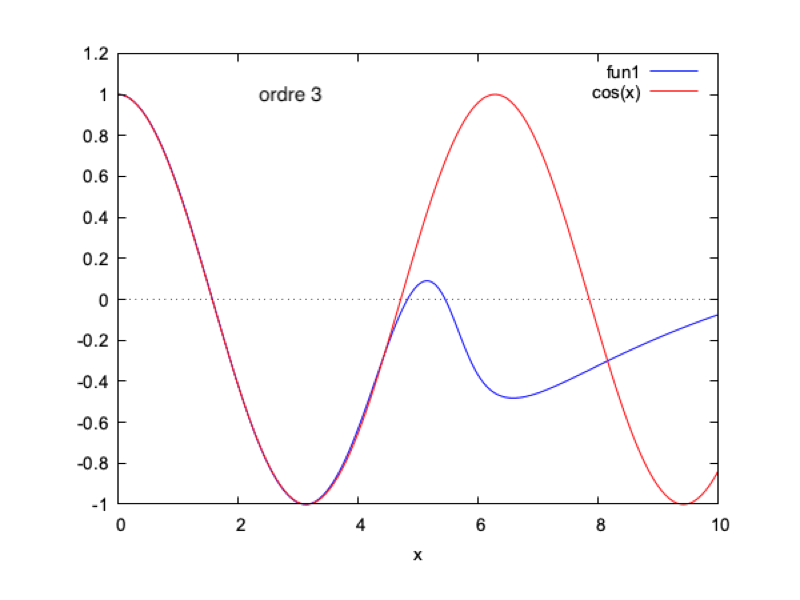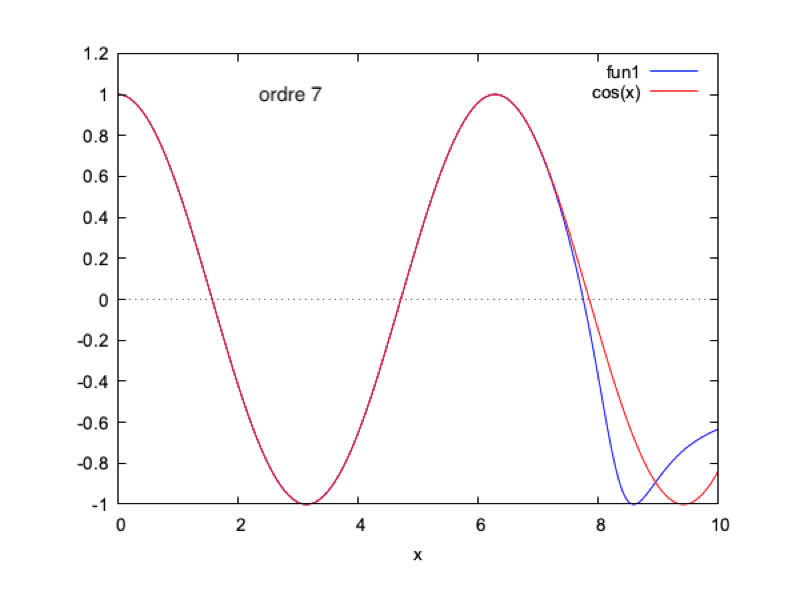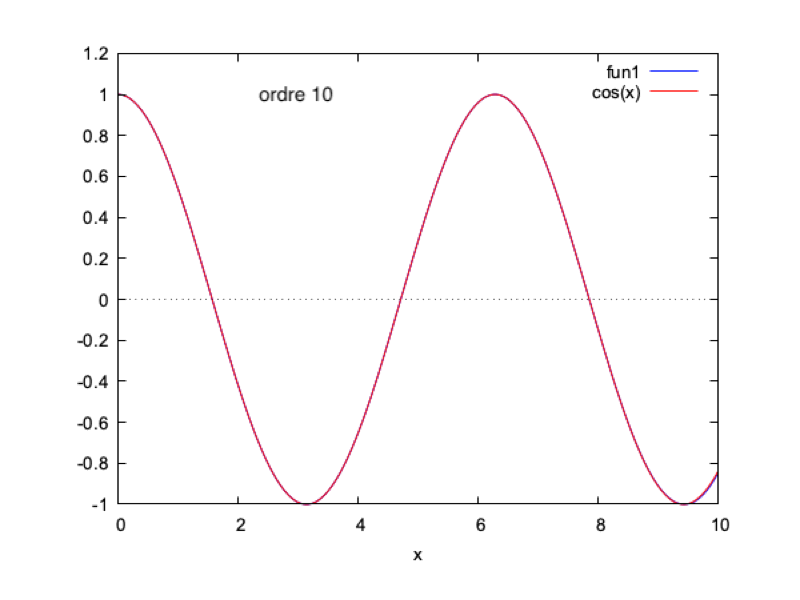
Donc $ ϕ_0(x) = u_0+\dfrac{iku_0x}{1-ikL} = 1 + \dfrac{ikx}{1-ikL} $
or $ kL=1 $ ie $ L=\dfrac{1}{k} $donc $ ϕ_0(x) = 1 - \dfrac{kx}{2} + \dfrac{ikx}{2} $
On a : $ |ϕ_0|=\sqrt {1-(\dfrac{kx}{2})^2 + (\dfrac{kx}{2})^2} = \sqrt {1-kx+\dfrac{k^2x^2}{2}} $
donc $ H = \dfrac{1+\dfrac{kx}{2}}{\sqrt {1-kx+\dfrac{k^2x^2}{2}}}= \dfrac{Re(ϕ_0)}{|ϕ_0|} $
donc $ \boxed{h(x,t)= \dfrac {1+\dfrac {kx}{2}} {\sqrt {1-kx+\dfrac {k^2x^2} {2}}} cos(\omega t) } $
Ordre 1 :
$ \dfrac{\partial^2 ϕ_1}{\partial x^2} = -\dfrac{\partial^2 u_0}{\partial x^2} - k^2 ϕ_0 $
$ \Rightarrow $ $ \dfrac{\partial ϕ_1}{\partial x} = -\dfrac{\partial u_0}{\partial x} - k^2 \int ϕ_0 + A_1 $ donc $ ϕ_1(x)=-u_0-k^2 \iint ϕ_0 +A_1x + B_1 $
or $ \iint ϕ_0 = -\dfrac{u_0x^2}{2}+\dfrac{iku_0x^3}{6(1-ikL)} $
donc pour $ u_0=1 $: $ ϕ_1(x)=-1-\dfrac{k^2x^2}{2}+\dfrac{ik^3x^3}{6(1-ikL)} + A_1x + B_1 $
- $ x=0 \rightarrow \phi_1(x)=1 \rightarrow B_1=0 $
- $ x=L : \dfrac{\partial ϕ}{\partial x}=ik\phi=-\dfrac{17}{12}ik+\dfrac{k}{12}+A_1i~~(1) $
Or on a également $ \dfrac{\partial ϕ}{\partial x}=-k^2x+\dfrac{k^3}{4}x^2-\dfrac{ik^3}{4}x^2 + A_1 $ donc pour $ x=L : \dfrac{\partial ϕ}{\partial x}= -k+\dfrac{k}{4}-\dfrac{ik}{4}+A_1~~(2) $
Donc $ (1)=(2) \Rightarrow -\dfrac{17}{12}ik+\dfrac{k}{12}+A_1L=-k+\dfrac{k}{4}-\dfrac{ik}{4}+A_1~ie~A_1=k-\dfrac{1}{6}iK $
D'où $ \phi_1(x)= -1-\dfrac{k^2x^2}{2}+\dfrac{(k^3-ik^3)}{12}x^3+(k-\dfrac{ik}{6})x $
On continue pendant un nombre n d'itérations. On pourra ensuite calculer $ \boxed{h=\dfrac{Re(\phi_0+...+\phi_n)}{|\phi_0+...+\phi_n|}} $
Nous faisons ce calcul sur Maxima et nous obtenons les courbes suivantes (mises en regard de la solution analytique pour $ k=1 $ et $ \omega=1 $, à $ t=0 $) :
Cas n°2
Nous étudions maintenant un canal uniforme unidimensionnel, avec une réflexion totale en amont $ ϕ_x=0 $ et une condition de flux aval $ ϕ_x=ik(2−ϕ) $
Comme dans le cas n°1, l'équation de Berkhoff se simplifie comme suivant: $ \frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $ Seules les conditions limites changent.
Solution analytique
L'équation caractéristique est la même que dans le cas n°1 : $ X^2 + k^2 = 0 $
La solution est de la forme $ Ae^{-ikx}+ Be^{ikx} $, avec A et B des constantes.
Détermination des constantes $ A $ et $ B $ grâce aux conditions limites :
- $ A=e^{2ikL} $
- $ B=1 $
Donc $ ϕ(x)=e^{ik(2L-x)}+e^{ikx} $
Ainsi $ ϕ(x,t)=e^{i[k(2L-x)-\omega t]}+e^{i(kx-\omega t)} $
D'où la hauteur d'eau est : $ \boxed{h(x,t)=Re(ϕ(x,t))=cos(k(2L-x)-\omega t)+cos(kx-\omega t)} $
Solution semi-analytique (homotopie)
Comme dans le cas n°1, la relation d'homotopie s'exprime comme suivant :
$ (1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0 $
Grâce au même raisonnement que ci-dessus, on obtient donc : $ (1−p)((ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...)-u_{0,xx})+p[ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)]=0 $
On développe de même en fonction des ordres de p (seules les conditions limites changent).
Ordre 0 :
On a $ ϕ_{0}=Ax+B+u_0 $
Détermination des constantes $ A $ et $ B $ grâce aux conditions limites :
- en amont : $ x=0 $ $ \Rightarrow $ $ \dfrac{\partial ϕ_0}{\partial x} = 0 = A $ donc $ A=0 $
- en aval : $ x=L $ $ \Rightarrow $ $ \dfrac{\partial ϕ_0}{\partial x} = ik(2-ϕ_0) = ik(2-AL-B-u_0) = A $ ie $ B=2-u_0 \rightarrow B=1 $
donc $ ϕ_{0}=1+u_0=2 $ d'où $ h=\dfrac{Re(\phi)}{|\phi|} = \dfrac{2}{\sqrt{2^2}} ie $ $ \fbox{h=1} $
Ordre 1 :
On a $ ϕ_{1}=u_0-k^2\iint ϕ_0+A_1x+B_1 $
or $ \iint ϕ_0= x^2 $ donc $ ϕ_1 = u_0-k^2x^2+A_1x+B_1 $
Détermination des constantes $ A_1 $ et $ B_1 $ grâce aux conditions limites :
- $ x=0 $$ \Rightarrow $ $ \dfrac{\partial ϕ_0}{\partial x} = 0 = A_1-2k^2x $ or $ x=0 $ donc $ A_1=0 $
- $ x=L $$ \Rightarrow $ $ \dfrac{\partial ϕ_1}{\partial x} = ik(2-ϕ_1) = ik(2-u_0-k^2L^2+A_1L+B_1) = A_1-2k^2L = 2-u_0-k^2L^2+B_1 = \dfrac{2kL}{i}=-2ikL $ donc $ B_1=-2ikL-2+u_0+k^2L^2 $
or $ kL=1 $ et $ u_0=1 $ donc $ B_1=-2i $
donc $ ϕ_1(x)=1-k^2x^2-2i $
Dès la deuxième itération , on peut voir l'évolution de la houle graphiquement (l'amont est à gauche) en calculant $ \Phi(x) =ϕ_0(x) + ϕ_1(x) $, puis $ h(x,t) $ :
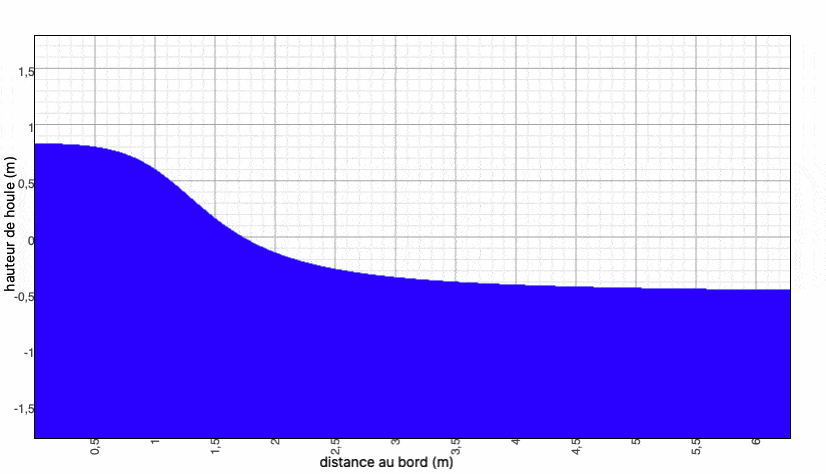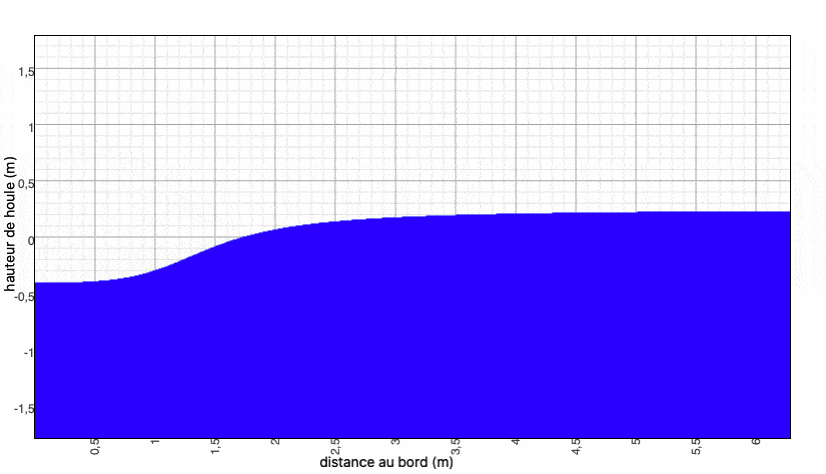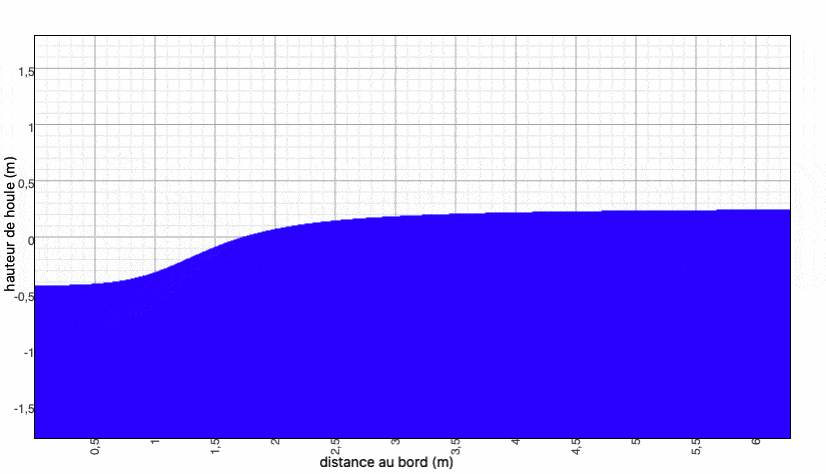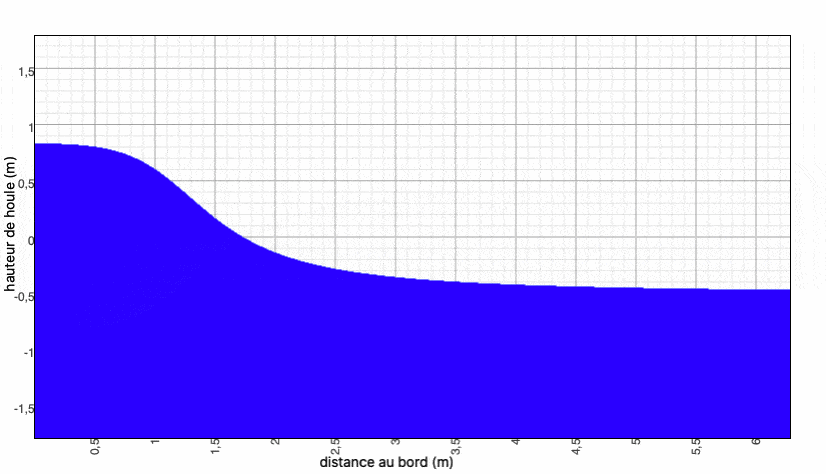
On continue pendant un nombre n d'itérations. On pourra ensuite calculer $ \boxed{h=\dfrac{Re(\phi_0+...+\phi_n)}{|\phi_0+...+\phi_n|}} $
Nous faisons ce calcul sur Maxima et nous obtenons les résultats suivants :
Cas n°3
Nous cherchons à modéliser un canal uniforme unidimensionnel avec une pente de fond constante avec l'entrée d'une onde de fréquence unitaire par l'aval $ ϕ=1 $ et une sortie libre en amont $ ϕ_x=ikϕ $.
Dans ce cas précis, l'équation de Berkhoff se simplifie comme suit:
$ \nabla (CC_g\nabla\phi)+k^2CC_g\phi=0 $
or $ CC_g=gH $ et $ H $ n'est pas constante car il s'agit d'une pente.
On prend donc $ H(x)=-px+h $ avec $ h $ la hauteur initiale et $ p $ la pente.
D'où $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $.
Solution analytique
On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
On prend comme changement de variable $ X=\dfrac{K}{P}(h-px) $
On a alors : $ pkX\dfrac{\partial^2\phi}{\partial X^2}+pK\dfrac{\partial\phi}{\partial X}+pkX\phi=0 $
En multipliant par X et en divisant par pK, on a $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $
On a donc la solution générale $ \phi(x)=A.J_0(x)+B.Y_0(x) $ avec $ J_0 $ une fonction de Bessel de 1ère espèce et $ Y_0 $ une fonction de Bessel de 2ème espèce.
D'après les conditions limites : $ \phi(0)=1 $ et $ \phi(x)=ik\phi $
On trouve :$ \phi(x) = \frac{J_0(x)*(Y_1(xL)-iY_0(xL)) + Y_0(x)*(J_1(xL)+iJ_0(xL))}{J_0(x_0)*(Y_1(xL)-iY_0(xL))+Y_0(x_0)*(J_1(xL)+iJ_0(xL))} $
Solution semi-analytique (homotopie)
Cas n°5
Le dernier cas concret que nous traitons est un domaine bidimensionnel plat avec une direction préférentielle des houles.
L'équation de Berkhoff se simplifie comme suivant pour un canal bidimensionnel :
$ \nabla (gH\nabla\phi)+k^2gH\phi=0 $
Dans ce cas précis, le fond est plat, d'où : $ \nabla \phi+k^2\phi=0 $
Ici, on ne peut pas trouver la solution analytique. On peut seulement approcher la solution grâce à une méthode de différences finies ou grâce à l'homotopie. Nous allons ici résoudre cette équation par homotopie (solution semi-analytique).
Solution semi-analytique (homotopie)
Les limites du modèle
Nous rencontrons 2 grands types de limitations : les limitations physiques ainsi que les limitations mathématiques
Limites physiques
- Le fond du canal influence la houle et réciproquement. Or, notre modèle ne prend notamment pas en compte des phénomènes tels que le transport des sédiments et des sables qui pourraient modifier le fond du canal et donc avoir une influence sur la houle.
- irrégularité du fond
- irrégularité u trait de côte
- Pourquoi l'onde serait pure ???????
- réalisme de certaines données (L=1m par exemple)
- la houle se différencie de la vague par son absence de relation au vent. Mais l'érosion est affectée par les 2 : vent et houle
Limites mathématiques
- beaucoup de variables sont considérées constantes ($ k,\omega,L etc $)
- on suppose une uniformité spatiale et temporelle du phénomène ?????
- l'ordre d'homotopie "n" influe beaucoup sur la qualité du modèle : divergence rapide si "n" petit
 S'abonner à un flux RSS
S'abonner à un flux RSS