Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/BRETON-NGUYEN-SALLES : Différence entre versions
(→Limites mathématiques) |
(→Solution semi-analytique (homotopie)) |
||
| (34 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | <html><iframe frameborder="0" width="480" height="270" src="https://www.dailymotion.com/embed/video/k2BqGkgrmrscSCw7A30 | + | <html><iframe frameborder="0" width="480" height="270" src="https://www.dailymotion.com/embed/video/k2BqGkgrmrscSCw7A30?queue-enable=false" allowfullscreen></iframe><br /><a href="https://dai.ly/k2BqGkgrmrscSCw7A30" target="_blank">Vidéo d'introduction</a> <i>par <a href="http://www.dailymotion.com/Wikhydro" target="_blank">Wikhydro</a></i></html> |
Modélisation de la houle par homotopie : une brève introduction | Modélisation de la houle par homotopie : une brève introduction | ||
|} | |} | ||
| Ligne 10 : | Ligne 10 : | ||
Nous nous placerons dans l'hypothèse d'ondes longues et nous étudierons différents cas concrets de géométries et de conditions aux limites. | Nous nous placerons dans l'hypothèse d'ondes longues et nous étudierons différents cas concrets de géométries et de conditions aux limites. | ||
| − | == '''Cas n°1''' == | + | == '''Cas n°1 : canal uniforme unidimensionnel avec sortie libre en amont''' == |
Cette situation traite un canal uniforme unidimensionnel plat de longueur L avec l'entrée d'une onde de fréquence unitaire <math>ϕ=1</math> par l'aval et une sortie libre en amont <math>ϕ_x=ikϕ</math>. | Cette situation traite un canal uniforme unidimensionnel plat de longueur L avec l'entrée d'une onde de fréquence unitaire <math>ϕ=1</math> par l'aval et une sortie libre en amont <math>ϕ_x=ikϕ</math>. | ||
| Ligne 27 : | Ligne 27 : | ||
Détermination des constantes A et B grâce aux conditions limites : | Détermination des constantes A et B grâce aux conditions limites : | ||
* <math>ϕ(x=0)=1</math> → <math>A+B=1</math> | * <math>ϕ(x=0)=1</math> → <math>A+B=1</math> | ||
| − | * <math>\dfrac{\partial ϕ}{\partial x}(x= | + | * <math>\dfrac{\partial ϕ}{\partial x}(x=L)=ik \phi</math> → <math>A=0</math> et <math>B=1</math> |
| Ligne 48 : | Ligne 48 : | ||
<span style="color: DeepPink;"><math>(1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0</math></span><br> | <span style="color: DeepPink;"><math>(1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0</math></span><br> | ||
Or: | Or: | ||
| + | * <math> u_0 =0 </math> | ||
* <math>ϕ(x,p) = \sum_{n=0}^∞ p^nϕ_n = ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... </math> | * <math>ϕ(x,p) = \sum_{n=0}^∞ p^nϕ_n = ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... </math> | ||
*<math>ϕ_{xx}(x,p) = ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...</math> | *<math>ϕ_{xx}(x,p) = ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...</math> | ||
D'où : | D'où : | ||
| − | <math>(1−p) | + | <math>(1−p)(ϕ_{xx})+p(ϕ_{xx}+k^2ϕ)=0</math>, c'est-à-dire : |
| + | <span style="color: Red;"><math>ϕ_{xx}+p k^2ϕ=0</math> </span><br><br> | ||
| + | Soit en développant : <math>ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+p k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)=0</math> | ||
| − | On développe ensuite en fonction des ordres de p. <br> | + | On "développe" ensuite en fonction des ordres de p. <br> |
<span style="color: Coral;">Ordre 0 : </span><br> | <span style="color: Coral;">Ordre 0 : </span><br> | ||
| − | <math>ϕ_ | + | <math>ϕ_{0,xx}=0 \implies \dfrac{\partial ϕ_0}{\partial x} = A \implies ϕ_0(x) = Ax + B</math> <br> |
| − | + | ||
| − | + | ||
| − | + | ||
Détermination des constantes A et B : <br> | Détermination des constantes A et B : <br> | ||
| − | * <math>ϕ(0) = 1 | + | * <math>ϕ(0) = 1 \implies B=1 </math> <br> |
| − | * <math>\dfrac{\partial ϕ}{\partial x} = ikϕ </math> or <math>ϕ = Ax + B | + | * <math>\dfrac{\partial ϕ}{\partial x} = ikϕ </math> or <math>ϕ = Ax + B</math> et <math>\dfrac{\partial ϕ}{\partial x} = A </math> <br> d'où pour <math>x=L</math>, <math>A = ik(AL+B) \implies A = \dfrac{ik}{1-ikL} = \dfrac{ik}{1-i} </math> avec <math>kL=1</math> <br> |
| − | Donc <math>ϕ_0(x) | + | Donc <math>ϕ_0(x) = 1 + \dfrac{ikx}{1-i}</math> <br> |
or <math>kL=1</math> ie <math>L=\dfrac{1}{k}</math>donc <span style="color: DodgerBlue;"><math>ϕ_0(x) = 1 - \dfrac{kx}{2} + \dfrac{ikx}{2}</math></span> <br> | or <math>kL=1</math> ie <math>L=\dfrac{1}{k}</math>donc <span style="color: DodgerBlue;"><math>ϕ_0(x) = 1 - \dfrac{kx}{2} + \dfrac{ikx}{2}</math></span> <br> | ||
| − | On a : <math>H = \Re(ϕ_0) = 1 | + | On a : <math>H = \Re(ϕ_0) = 1-\dfrac{kx}{2}</math> <br> |
| − | donc <span style="color: DodgerBlue;"><math>\boxed{h(x,t)= 1 | + | donc <span style="color: DodgerBlue;"><math>\boxed{h(x,t)= 1-\dfrac {kx}{2} cos(\omega t)}</math></span> <br> |
<span style="color: Coral;">Ordre 1 : </span><br> | <span style="color: Coral;">Ordre 1 : </span><br> | ||
| − | <math>\dfrac{\partial^2 ϕ_1}{\partial x^2} = | + | <math>\dfrac{\partial^2 ϕ_1}{\partial x^2} = k^2 ϕ_0 \implies ϕ_1(x)=-k^2 \iint ϕ_0 +A_1x + B_1</math> <br> |
| − | + | or <math>\iint ϕ_0 = \dfrac{x^2}{2}-\dfrac{ikx^3}{6(1-i)}</math> <br> | |
| − | or <math>\iint ϕ_0 = | + | donc : <math>ϕ_1(x)=-\dfrac{k^2x^2}{2}+\dfrac{ik^3x^3}{6(1-i)} + A_1x + B_1</math> |
| − | donc | + | |
| − | *<math>x=0 \ | + | *<math>x=0 \implies \phi(x)=\phi_0(x) +p\phi_1(x) \implies B_1=0</math> <br> |
| − | *<math>x=L : \dfrac{\partial ϕ}{\partial x}=ik\phi | + | *<math>x=L : \dfrac{\partial ϕ(x=L)}{\partial x}=ik\phi(x=L) \implies A_1=\dfrac{k}{2}-\dfrac{iK}{3}</math> <br> |
| − | + | ||
| − | + | ||
| − | D'où <span style="color: DodgerBlue;"><math>\phi_1(x)= | + | D'où <span style="color: DodgerBlue;"><math>\phi_1(x)= \dfrac{(k^3-ik^3)}{12}x^3-\dfrac{k^2}{2}x^2+(\dfrac{k}{2}-\dfrac{iK}{3})x</math></span> <br> |
| + | |||
On continue pendant un nombre n d'itérations. On pourra ensuite calculer <span style="color: DodgerBlue;"><math>\boxed{h(x,t)=\Re((\phi_0+...+\phi_n)e^{-i\omega t})}</math></span> <br> | On continue pendant un nombre n d'itérations. On pourra ensuite calculer <span style="color: DodgerBlue;"><math>\boxed{h(x,t)=\Re((\phi_0+...+\phi_n)e^{-i\omega t})}</math></span> <br> | ||
Nous faisons ce calcul sur Maxima et nous obtenons les courbes suivantes (mises en regard de la solution analytique pour <math>k=1</math> et <math>\omega=1</math>, à <math>t=0</math>) : | Nous faisons ce calcul sur Maxima et nous obtenons les courbes suivantes (mises en regard de la solution analytique pour <math>k=1</math> et <math>\omega=1</math>, à <math>t=0</math>) : | ||
| Ligne 92 : | Ligne 90 : | ||
[[File:Cas1_homotopie_ordres0à10_sans_module.gif]] | [[File:Cas1_homotopie_ordres0à10_sans_module.gif]] | ||
| − | |||
| − | |||
| − | |||
==== Etude de sensibilité des paramètres ==== | ==== Etude de sensibilité des paramètres ==== | ||
| Ligne 112 : | Ligne 107 : | ||
L'amplitude est supposée constante ici, mais ce n'est pas le cas dans la réalité : à faible profondeur non seulement les vagues se rapprochent et ralentissent mais aussi leur hauteur augmente. | L'amplitude est supposée constante ici, mais ce n'est pas le cas dans la réalité : à faible profondeur non seulement les vagues se rapprochent et ralentissent mais aussi leur hauteur augmente. | ||
| − | == '''Cas n°2''' == | + | == '''Cas n°2 : canal uniforme unidimensionnel avec réflexion totale en amont''' == |
Nous étudions maintenant un canal uniforme unidimensionnel, avec une réflexion totale en amont <math>ϕ_x=0</math> et une condition de flux aval <math>ϕ_x=ik(2−ϕ)</math> | Nous étudions maintenant un canal uniforme unidimensionnel, avec une réflexion totale en amont <math>ϕ_x=0</math> et une condition de flux aval <math>ϕ_x=ik(2−ϕ)</math> | ||
| Ligne 148 : | Ligne 143 : | ||
Grâce au même raisonnement que ci-dessus, on obtient donc : | Grâce au même raisonnement que ci-dessus, on obtient donc : | ||
| − | <math>(1−p)((ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...) | + | <math>(1−p)((ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...))+p[ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)]=0</math> |
| Ligne 154 : | Ligne 149 : | ||
On développe de même en fonction des ordres de p (seules les conditions limites changent). <br> | On développe de même en fonction des ordres de p (seules les conditions limites changent). <br> | ||
<span style="color: Coral;">Ordre 0 : </span><br> | <span style="color: Coral;">Ordre 0 : </span><br> | ||
| − | On a <math>ϕ_{0}=Ax+B | + | On a <math>ϕ_{0}=Ax+B</math> |
Détermination des constantes <math>A</math> et <math>B</math> grâce aux conditions limites : | Détermination des constantes <math>A</math> et <math>B</math> grâce aux conditions limites : | ||
| − | * en aval : <math>x=L | + | * en aval : <math>x=L \implies \dfrac{\partial ϕ_0}{\partial x} = 0 \implies A=0 </math> <br> |
| − | * en amont : <math>x=0 | + | * en amont : <math>x=0 \implies \dfrac{\partial ϕ_0}{\partial x} = ik(2-\phi_0) = ik(2-Ax-B)=A~ie~ik(2-B)=0~ie~B=2</math> |
| − | donc <span style="color: DodgerBlue;"><math>\boxed{ϕ_{0} | + | donc <span style="color: DodgerBlue;"><math>\boxed{ϕ_{0}=2}</math></span> <br> |
<span style="color: Coral;">Ordre 1 : </span><br> | <span style="color: Coral;">Ordre 1 : </span><br> | ||
| − | On a <math>ϕ_{1}= | + | On a <math>ϕ_{1}=-k^2\iint ϕ_0+A_1x+B_1</math> <br> |
| − | or <math>\iint ϕ_0= x^2 </math> donc <math>ϕ_1(x) = | + | or <math>\iint ϕ_0= x^2 </math> donc <math>ϕ_1(x) =-k^2x^2+A_1x+B_1</math> <br> |
or | or | ||
| − | * en aval : <math>x=L | + | * en aval : <math>x=L \implies A_1=2k</math> <br> |
| − | * en amont : <math>x=0 | + | * en amont : <math>x=0 \implies \dfrac{\partial \phi}{\partial x}= \dfrac{\partial ϕ_0}{\partial x} + p \dfrac{\partial ϕ_1}{\partial x} = ik(2-\phi) \implies B=2i</math> <br> |
| − | + | ||
| − | + | ||
| − | D'où <span style="color: DodgerBlue;"><math>\boxed{ϕ_1(x)=-k^2x^2+2kx+2i | + | D'où <span style="color: DodgerBlue;"><math>\boxed{ϕ_1(x)=-k^2x^2+2kx+2i}</math></span><br> |
On continue pendant un nombre n d'itérations. On pourra ensuite calculer <span style="color: DodgerBlue;"><math>\boxed{\Re((\phi_0+...+\phi_n)e^{-i\omega t})}</math></span> <br> | On continue pendant un nombre n d'itérations. On pourra ensuite calculer <span style="color: DodgerBlue;"><math>\boxed{\Re((\phi_0+...+\phi_n)e^{-i\omega t})}</math></span> <br> | ||
| Ligne 184 : | Ligne 177 : | ||
N.B. La phase et l'amplitude de la solution analytique sont ajustées respectivement à -3,45 et 2,42 afin d'obtenir une bonne superposition des données. Les raisons de cet ajustement nous sont inconnues. | N.B. La phase et l'amplitude de la solution analytique sont ajustées respectivement à -3,45 et 2,42 afin d'obtenir une bonne superposition des données. Les raisons de cet ajustement nous sont inconnues. | ||
| − | == '''Cas n°3''' == | + | == '''Cas n°3 : canal uniforme unidimensionnel avec pente de fond constante et sortie libre en amont''' == |
Nous cherchons à modéliser un canal uniforme unidimensionnel avec une pente de fond constante avec l'entrée d'une onde de fréquence unitaire par l'aval <math>ϕ=1</math> et une sortie libre en amont <math>ϕ_x=ikϕ</math>. | Nous cherchons à modéliser un canal uniforme unidimensionnel avec une pente de fond constante avec l'entrée d'une onde de fréquence unitaire par l'aval <math>ϕ=1</math> et une sortie libre en amont <math>ϕ_x=ikϕ</math>. | ||
| Ligne 209 : | Ligne 202 : | ||
On trouve :<math>\phi(x) = \frac{J_0(x)*(Y_1(x_L)-iY_0(x_L)) + Y_0(x)*(J_1(x_L)+iJ_0(x_L))}{J_0(x_0)*(Y_1(x_L)-iY_0(x_L))+Y_0(x_0)*(J_1(x_L)+iJ_0(x_L))} </math> , soit, avec <math>\widetilde{Y} = Y_1(x_L)-iY_0(x_L)</math> et <math>\widetilde{J}=J_1(x_L)+iJ_0(x_L)</math> : | On trouve :<math>\phi(x) = \frac{J_0(x)*(Y_1(x_L)-iY_0(x_L)) + Y_0(x)*(J_1(x_L)+iJ_0(x_L))}{J_0(x_0)*(Y_1(x_L)-iY_0(x_L))+Y_0(x_0)*(J_1(x_L)+iJ_0(x_L))} </math> , soit, avec <math>\widetilde{Y} = Y_1(x_L)-iY_0(x_L)</math> et <math>\widetilde{J}=J_1(x_L)+iJ_0(x_L)</math> : | ||
<math>\phi(x) = \frac{J_0(x)*\widetilde{Y} + Y_0(x)*\widetilde{J}}{J_0(x_0)*\widetilde{Y}+Y_0(x_0)*\widetilde{J}} </math> | <math>\phi(x) = \frac{J_0(x)*\widetilde{Y} + Y_0(x)*\widetilde{J}}{J_0(x_0)*\widetilde{Y}+Y_0(x_0)*\widetilde{J}} </math> | ||
| + | |||
| + | [[File:cas3_analytique4.png]] | ||
| + | |||
| + | N.B. La pente du fond n'est pas représentée ici. | ||
==== Solution semi-analytique (homotopie) ==== | ==== Solution semi-analytique (homotopie) ==== | ||
| Ligne 244 : | Ligne 241 : | ||
D'où : <span style="color: DodgerBlue;"><math>\boxed{\phi_1(x)=(ax+1-h)\phi_0+a(\dfrac{ikx^2}{2(1-ikL)}x^2+x)-k^2(\dfrac{ikx^3}{6(1-ikL)}x^3+\dfrac{x^2}{2})+Ax+B}</math></span> <br> | D'où : <span style="color: DodgerBlue;"><math>\boxed{\phi_1(x)=(ax+1-h)\phi_0+a(\dfrac{ikx^2}{2(1-ikL)}x^2+x)-k^2(\dfrac{ikx^3}{6(1-ikL)}x^3+\dfrac{x^2}{2})+Ax+B}</math></span> <br> | ||
| − | == '''Cas n°5''' == | + | Les graphes donnés par Maxima sont déconcertants (pour l'instant): |
| + | |||
| + | Graphe avec prise en compte du module de <math>\phi</math> | ||
| + | La solution homotopique n'est même pas calculée. | ||
| + | |||
| + | [[File:cas3_loupé.png]] | ||
| + | |||
| + | |||
| + | Graphe sans prise en compte du module de <math>\phi</math> | ||
| + | |||
| + | [[File:cas3_sans_module.png]] | ||
| + | |||
| + | == '''Cas n°5 : domaine bidimensionnel plat avec direction préférentielle des houles''' == | ||
Le dernier cas concret que nous traitons est un domaine bidimensionnel plat avec une direction préférentielle des houles. | Le dernier cas concret que nous traitons est un domaine bidimensionnel plat avec une direction préférentielle des houles. | ||
| Ligne 258 : | Ligne 267 : | ||
On a <math>\nabla \phi(x,y)+k^2\phi(x,y)=0 ~ie~ \dfrac{\partial^2\phi}{\partial x^2}+\dfrac{\partial^2\phi}{\partial y^2}+k^2\phi(x,y)=0</math> <br> | On a <math>\nabla \phi(x,y)+k^2\phi(x,y)=0 ~ie~ \dfrac{\partial^2\phi}{\partial x^2}+\dfrac{\partial^2\phi}{\partial y^2}+k^2\phi(x,y)=0</math> <br> | ||
Donc on obtient la relation homotopique suivante : <math>(1-p)(\phi_{xx}+\phi_{yy})+p(\phi_{xx}+\phi_{yy}+k^2\phi)=0</math> <br> | Donc on obtient la relation homotopique suivante : <math>(1-p)(\phi_{xx}+\phi_{yy})+p(\phi_{xx}+\phi_{yy}+k^2\phi)=0</math> <br> | ||
| + | |||
| + | |||
| + | Une idée de développement peut être de considérer l'équation de Berkhoff, simplifiée en Helmholtz : | ||
| + | |||
| + | [[File:cas5_biais.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | Et de faire un changement de repère de façon à obtenir : | ||
| + | |||
| + | |||
| + | |||
| + | [[File:cas5_droit.jpg]] | ||
== '''Les limites du modèle et applications ''' == | == '''Les limites du modèle et applications ''' == | ||
| Ligne 282 : | Ligne 304 : | ||
==== Limites mathématiques ==== | ==== Limites mathématiques ==== | ||
| − | * Beaucoup de variables sont considérées constantes (<math>k,\omega,L | + | * Beaucoup de variables sont considérées constantes (<math>k,\omega,L</math>etc), afin de limiter la complexité du modèle. |
* on suppose une uniformité spatiale et temporelle du phénomène : La zone génératrice de la houle est supposée être à un seul endroit et constante. On peut ainsi prédire l'effet d'une houle moyenne (en ondes longues, donc à faible profondeur), mais le pouvoir érosif de grandes crêtes n'est pas calculé. | * on suppose une uniformité spatiale et temporelle du phénomène : La zone génératrice de la houle est supposée être à un seul endroit et constante. On peut ainsi prédire l'effet d'une houle moyenne (en ondes longues, donc à faible profondeur), mais le pouvoir érosif de grandes crêtes n'est pas calculé. | ||
* l'ordre d'homotopie "n" influe beaucoup sur la qualité du modèle : La divergence est rapide si "n" est petit. | * l'ordre d'homotopie "n" influe beaucoup sur la qualité du modèle : La divergence est rapide si "n" est petit. | ||
Version actuelle en date du 19 août 2020 à 11:54
Notre travail a pour but de modéliser l'impact du changement climatique sur les côtes, en quantifiant l'impact des houles sur le littoral.
Pour modéliser les houles, nous utilisons le modèle de Berkhoff aussi appelé équation de pente douce, obtenu en 1972. Ce modèle est une équation aux dérivées partielles, que nous nous proposons de résoudre par une méthode analytique pour les cas simples et semi-analytique pour les cas plus complexes.
Nous nous placerons dans l'hypothèse d'ondes longues et nous étudierons différents cas concrets de géométries et de conditions aux limites.
[modifier] Cas n°1 : canal uniforme unidimensionnel avec sortie libre en amont
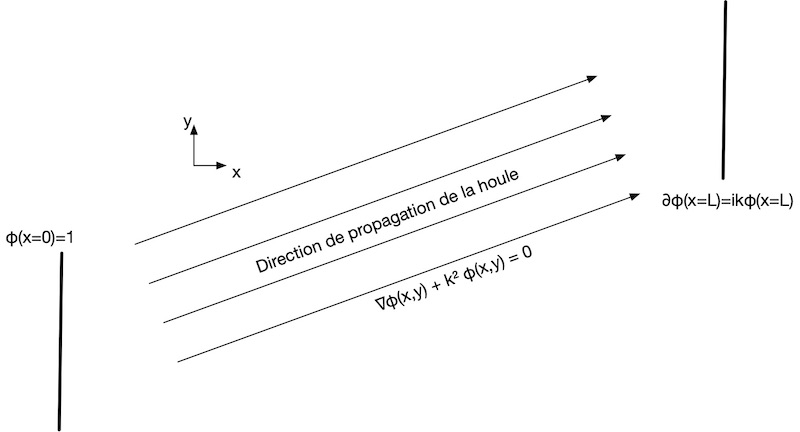
Cette situation traite un canal uniforme unidimensionnel plat de longueur L avec l'entrée d'une onde de fréquence unitaire $ ϕ=1 $ par l'aval et une sortie libre en amont $ ϕ_x=ikϕ $.
Dans ce cas précis, l'équation de Berkhoff se simplifie comme suit: $ \frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $
[modifier] Solution analytique
Nous résolvons l'équation caractéristique associée : $ X^2 + k^2 = 0 $
$ Δ = -4k^2 $ d'où $ λ_1 = -ik $ et $ λ_2 = ik $
donc la solution est de la forme $ Ae^{-ikx}+ Be^{ikx} $, avec A et B des constantes.
Détermination des constantes A et B grâce aux conditions limites :
- $ ϕ(x=0)=1 $ → $ A+B=1 $
- $ \dfrac{\partial ϕ}{\partial x}(x=L)=ik \phi $ → $ A=0 $ et $ B=1 $
donc $ ϕ(x)=e^{ikx} $
$ ϕ(x,t)=e^{i(kx-\omega t)} $
or $ H=\Re(ϕ) $ donc $ \fbox{h(x,t)=cos(kx-ωt)} $
N.B. : sur les graphiques, la valeur $ h(x)=0 $ représente le niveau moyen de la surface.
[modifier] Solution semi-analytique (homotopie)
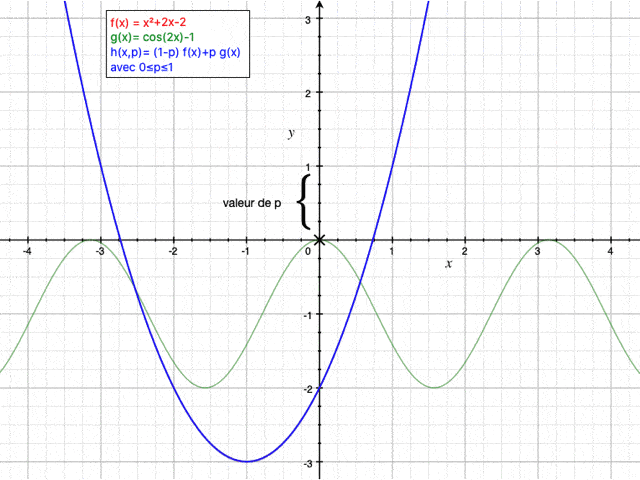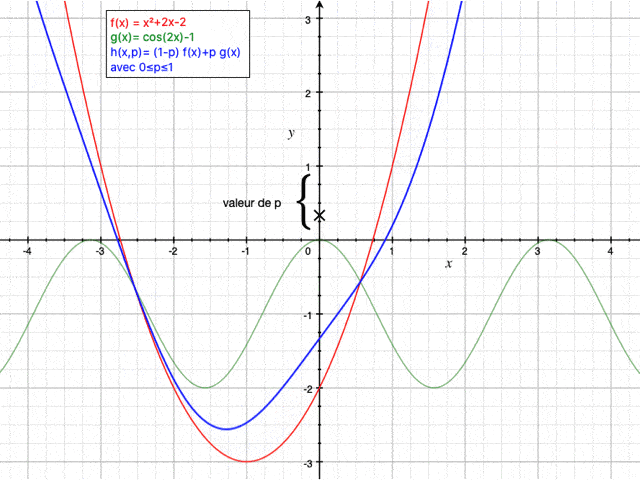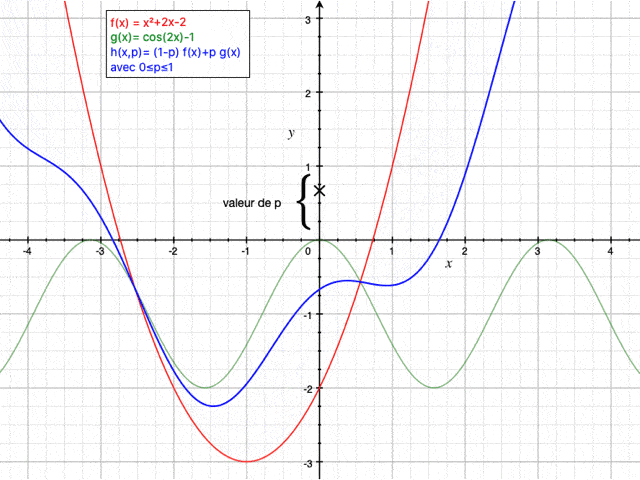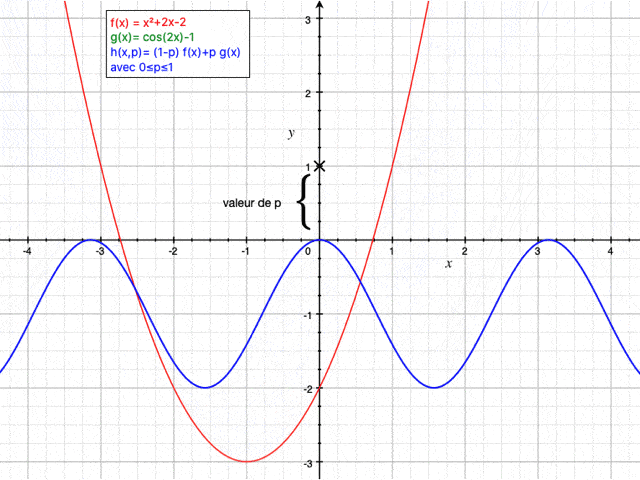
Le principe de la méthode d'homotopie est brièvement expliqué dans cette vidéo. Il s'agit de "passer" d'une fonction à une autre au travers d'un paramètre p variant de 0 à 1. Lorsque p vaut 0 et 1, $ h(x) $ est confondue avec respectivement $ f(x) $ et $ g(x) $.
Dans ce cas, la relation d'homotopie (ayant pour paramètre p entre 0 et 1) s'exprime comme ceci (on choisit la dérivée seconde comme opérateur linéaire et on part d'une solution initiale nulle):
$ (1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0 $
Or:
- $ u_0 =0 $
- $ ϕ(x,p) = \sum_{n=0}^∞ p^nϕ_n = ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $
- $ ϕ_{xx}(x,p) = ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+... $
D'où :
$ (1−p)(ϕ_{xx})+p(ϕ_{xx}+k^2ϕ)=0 $, c'est-à-dire :
$ ϕ_{xx}+p k^2ϕ=0 $
Soit en développant : $ ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+p k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)=0 $
On "développe" ensuite en fonction des ordres de p.
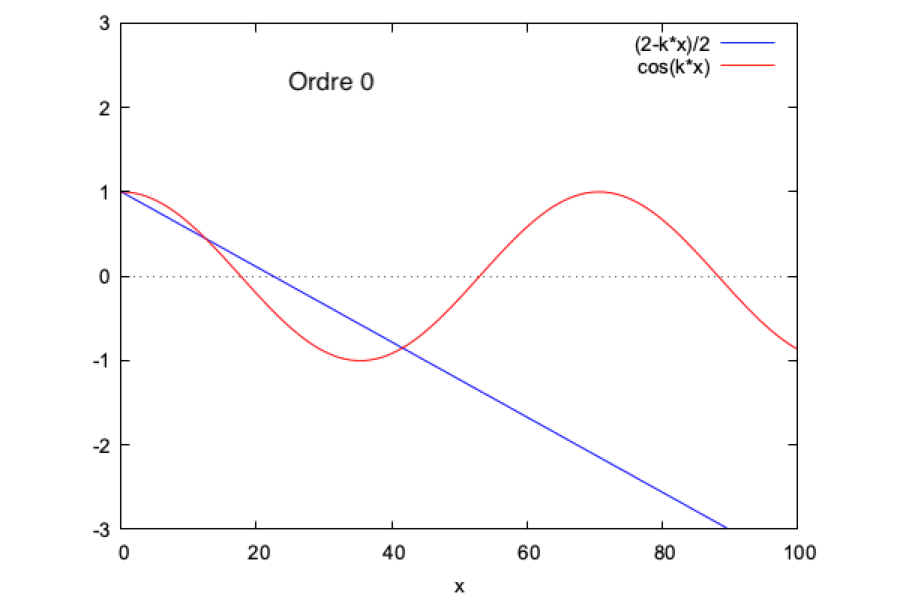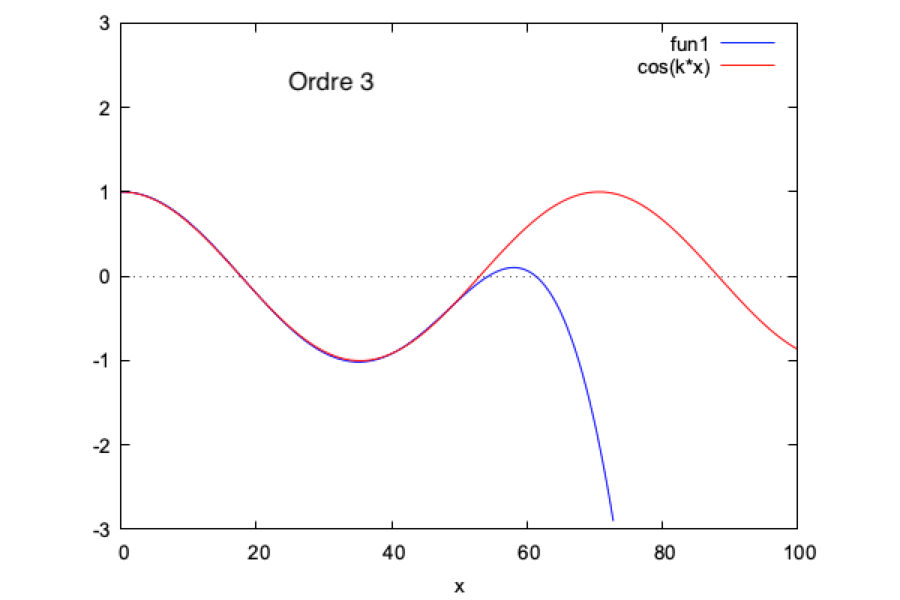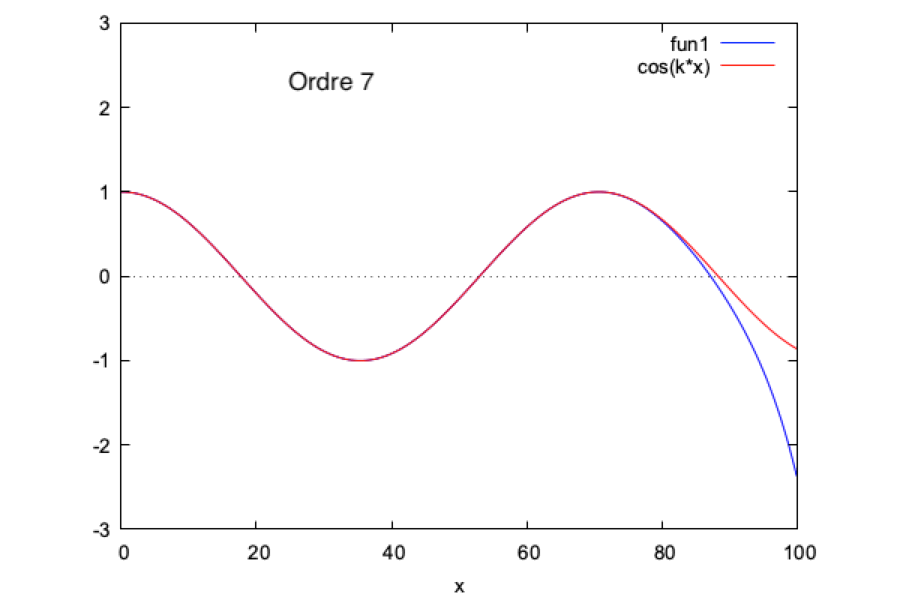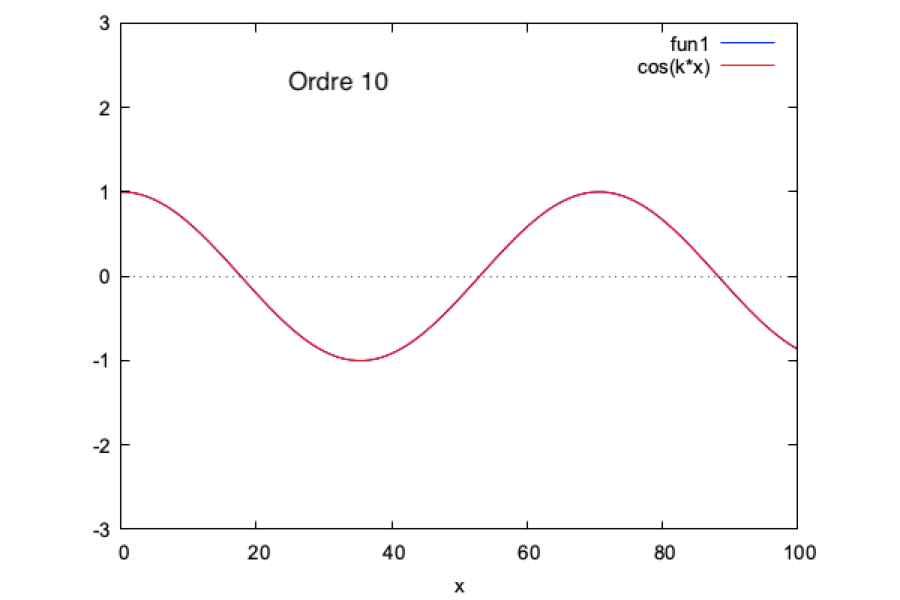
Ordre 0 :
$ ϕ_{0,xx}=0 \implies \dfrac{\partial ϕ_0}{\partial x} = A \implies ϕ_0(x) = Ax + B $
Détermination des constantes A et B :
- $ ϕ(0) = 1 \implies B=1 $
- $ \dfrac{\partial ϕ}{\partial x} = ikϕ $ or $ ϕ = Ax + B $ et $ \dfrac{\partial ϕ}{\partial x} = A $
d'où pour $ x=L $, $ A = ik(AL+B) \implies A = \dfrac{ik}{1-ikL} = \dfrac{ik}{1-i} $ avec $ kL=1 $
Donc $ ϕ_0(x) = 1 + \dfrac{ikx}{1-i} $
or $ kL=1 $ ie $ L=\dfrac{1}{k} $donc $ ϕ_0(x) = 1 - \dfrac{kx}{2} + \dfrac{ikx}{2} $
On a : $ H = \Re(ϕ_0) = 1-\dfrac{kx}{2} $
donc $ \boxed{h(x,t)= 1-\dfrac {kx}{2} cos(\omega t)} $
Ordre 1 :
$ \dfrac{\partial^2 ϕ_1}{\partial x^2} = k^2 ϕ_0 \implies ϕ_1(x)=-k^2 \iint ϕ_0 +A_1x + B_1 $
or $ \iint ϕ_0 = \dfrac{x^2}{2}-\dfrac{ikx^3}{6(1-i)} $
donc : $ ϕ_1(x)=-\dfrac{k^2x^2}{2}+\dfrac{ik^3x^3}{6(1-i)} + A_1x + B_1 $
- $ x=0 \implies \phi(x)=\phi_0(x) +p\phi_1(x) \implies B_1=0 $
- $ x=L : \dfrac{\partial ϕ(x=L)}{\partial x}=ik\phi(x=L) \implies A_1=\dfrac{k}{2}-\dfrac{iK}{3} $
D'où $ \phi_1(x)= \dfrac{(k^3-ik^3)}{12}x^3-\dfrac{k^2}{2}x^2+(\dfrac{k}{2}-\dfrac{iK}{3})x $
On continue pendant un nombre n d'itérations. On pourra ensuite calculer $ \boxed{h(x,t)=\Re((\phi_0+...+\phi_n)e^{-i\omega t})} $
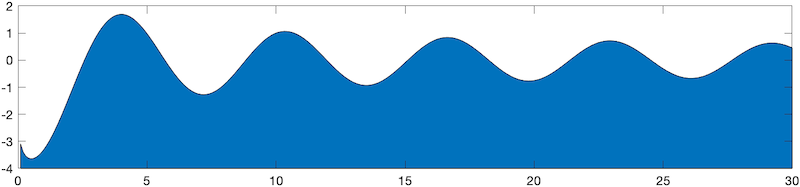
Nous faisons ce calcul sur Maxima et nous obtenons les courbes suivantes (mises en regard de la solution analytique pour $ k=1 $ et $ \omega=1 $, à $ t=0 $) :
[modifier] Etude de sensibilité des paramètres
Il y a deux paramètres qui interviennent dans notre équation : la fréquence $ \omega $ et la profondeur $ H $. On peut voir sur le graphique ci-dessous l'impact de la variation de la fréquence $ \omega $ sur la forme de la houle.
En effet, on remarque que plus la période est faible, plus les vagues sont rapprochées. Une brève discussion sur la période d'une houle est faite en fin d'article.
Sur le prochain graphique, on observe l'impact de la profondeur $ H $ sur la houle.
On remarque que plus la profondeur est faible plus les vagues se rapprochent et plus elles ralentissent, à la différence d'un simple changement de période. L'amplitude est supposée constante ici, mais ce n'est pas le cas dans la réalité : à faible profondeur non seulement les vagues se rapprochent et ralentissent mais aussi leur hauteur augmente.
[modifier] Cas n°2 : canal uniforme unidimensionnel avec réflexion totale en amont
Nous étudions maintenant un canal uniforme unidimensionnel, avec une réflexion totale en amont $ ϕ_x=0 $ et une condition de flux aval $ ϕ_x=ik(2−ϕ) $
Comme dans le cas n°1, l'équation de Berkhoff se simplifie comme suivant: $ \frac{\partial^2 ϕ}{\partial x^2} +k^2ϕ = 0 $ Seules les conditions limites changent.
[modifier] Solution analytique
L'équation caractéristique est la même que dans le cas n°1 : $ X^2 + k^2 = 0 $
La solution est de la forme $ Ae^{-ikx}+ Be^{ikx} $, avec A et B des constantes.
Détermination des constantes $ A $ et $ B $ grâce aux conditions limites :
- $ A=e^{2ikL} $
- $ B=1 $
Donc $ ϕ(x)=e^{ik(2L-x)}+e^{ikx} $
La solution est simplifiée à une amplitude et une phase nulles. Cependant on constate qu'ajouter une amplitude $ U $ et une phase $ \Phi $ ne change pas cette solution.
Ainsi $ ϕ(x,t)=e^{i[k(2L-x)-\omega t]}+e^{i(kx-\omega t)} $
D'où la hauteur d'eau est : $ \boxed{h(x,t)=\Re(ϕ(x,t))=cos(k(2L-x)-\omega t)+cos(kx-\omega t)} $
[modifier] Solution semi-analytique (homotopie)
Comme dans le cas n°1, la relation d'homotopie s'exprime comme suivant :
$ (1−p)(ϕ_{xx}-u_{0,xx})+p(ϕ_{xx}+k^2ϕ)=0 $
Grâce au même raisonnement que ci-dessus, on obtient donc : $ (1−p)((ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...))+p[ϕ_{0,xx}(x)+pϕ_{1,xx}(x)+p^2ϕ_{2,xx}(x)+p^3ϕ_{3,xx}(x)+...+k^2(ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+...)]=0 $
On développe de même en fonction des ordres de p (seules les conditions limites changent).
Ordre 0 :
On a $ ϕ_{0}=Ax+B $
Détermination des constantes $ A $ et $ B $ grâce aux conditions limites :
- en aval : $ x=L \implies \dfrac{\partial ϕ_0}{\partial x} = 0 \implies A=0 $
- en amont : $ x=0 \implies \dfrac{\partial ϕ_0}{\partial x} = ik(2-\phi_0) = ik(2-Ax-B)=A~ie~ik(2-B)=0~ie~B=2 $
donc $ \boxed{ϕ_{0}=2} $
Ordre 1 :
On a $ ϕ_{1}=-k^2\iint ϕ_0+A_1x+B_1 $
or $ \iint ϕ_0= x^2 $ donc $ ϕ_1(x) =-k^2x^2+A_1x+B_1 $
or
- en aval : $ x=L \implies A_1=2k $
- en amont : $ x=0 \implies \dfrac{\partial \phi}{\partial x}= \dfrac{\partial ϕ_0}{\partial x} + p \dfrac{\partial ϕ_1}{\partial x} = ik(2-\phi) \implies B=2i $
D'où $ \boxed{ϕ_1(x)=-k^2x^2+2kx+2i} $
On continue pendant un nombre n d'itérations. On pourra ensuite calculer $ \boxed{\Re((\phi_0+...+\phi_n)e^{-i\omega t})} $
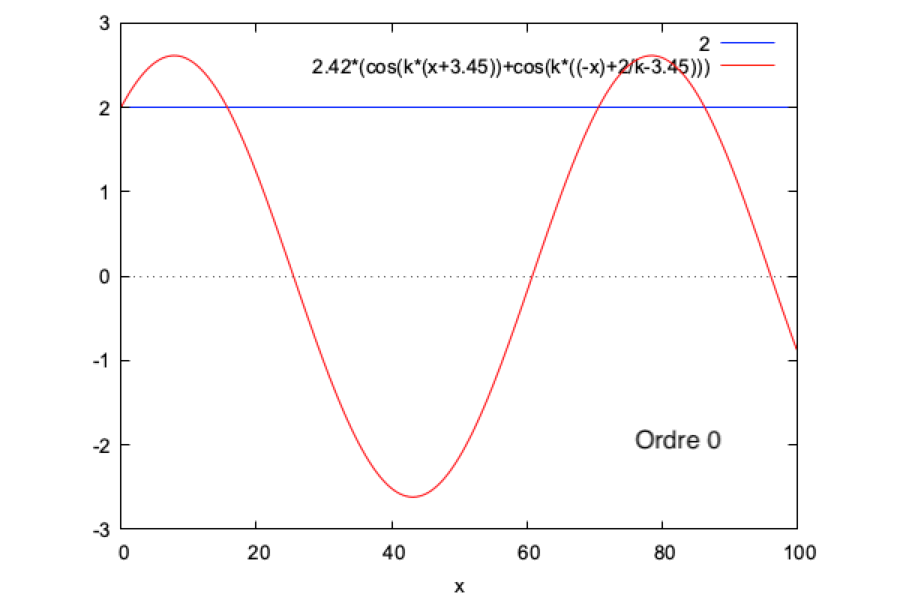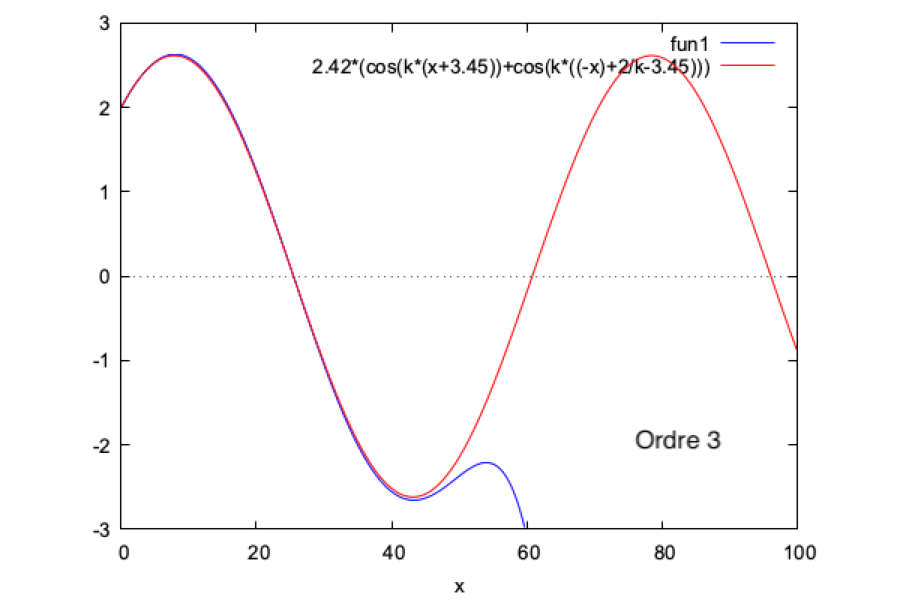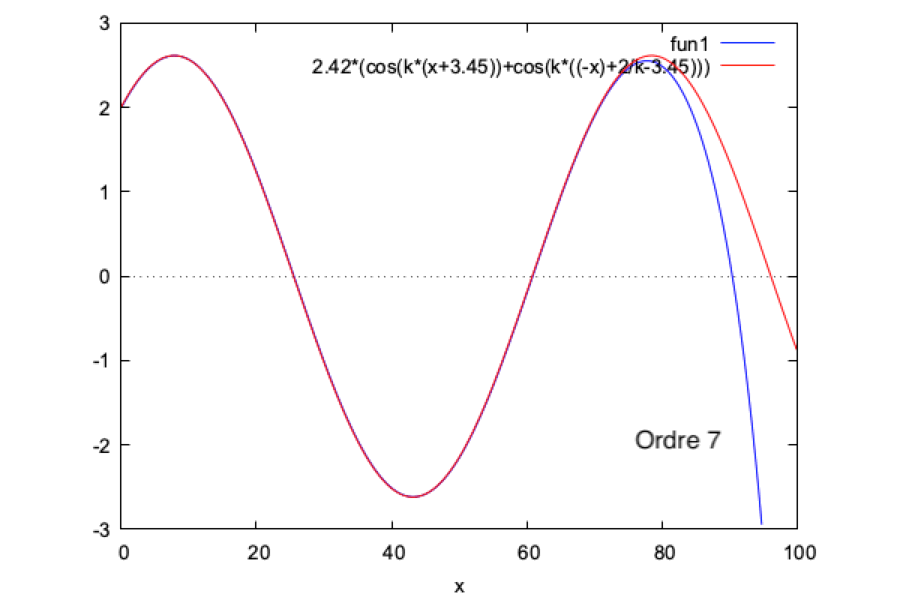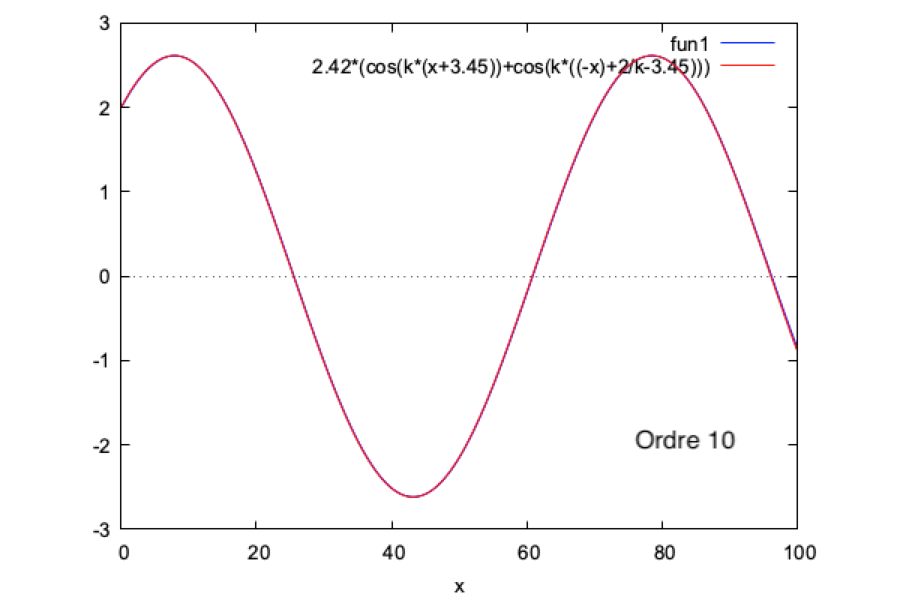
Nous faisons ce calcul sur Maxima et nous obtenons les résultats suivants :
N.B. La phase et l'amplitude de la solution analytique sont ajustées respectivement à -3,45 et 2,42 afin d'obtenir une bonne superposition des données. Les raisons de cet ajustement nous sont inconnues.
[modifier] Cas n°3 : canal uniforme unidimensionnel avec pente de fond constante et sortie libre en amont
Nous cherchons à modéliser un canal uniforme unidimensionnel avec une pente de fond constante avec l'entrée d'une onde de fréquence unitaire par l'aval $ ϕ=1 $ et une sortie libre en amont $ ϕ_x=ikϕ $.
Dans ce cas précis, l'équation de Berkhoff se simplifie comme suit:
$ \nabla (CC_g\nabla\phi)+k^2CC_g\phi=0 $
or $ CC_g=gH $ et $ H $ n'est pas constante car il s'agit d'une pente.
On prend donc $ H(x)=-ax+h $ avec $ h $ la hauteur initiale et $ a $ la pente.
D'où $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $.
[modifier] Solution analytique
On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
On prend comme changement de variable $ X=\dfrac{K}{P}(h-px) $
On a alors : $ pkX\dfrac{\partial^2\phi}{\partial X^2}+pK\dfrac{\partial\phi}{\partial X}+pkX\phi=0 $
En multipliant par X et en divisant par pK, on a $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $
On a donc la solution générale $ \phi(x)=A.J_0(x)+B.Y_0(x) $ avec $ J_0 $ une fonction de Bessel de 1ère espèce et $ Y_0 $ une fonction de Bessel de 2ème espèce.
D'après les conditions limites : $ \phi(0)=1 $ et $ \phi(x)=ik\phi $
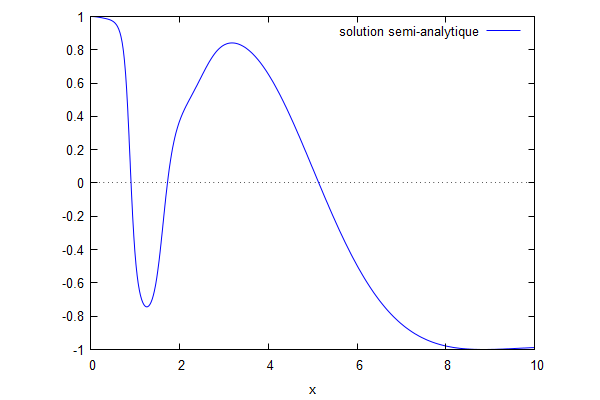
On trouve :$ \phi(x) = \frac{J_0(x)*(Y_1(x_L)-iY_0(x_L)) + Y_0(x)*(J_1(x_L)+iJ_0(x_L))}{J_0(x_0)*(Y_1(x_L)-iY_0(x_L))+Y_0(x_0)*(J_1(x_L)+iJ_0(x_L))} $ , soit, avec $ \widetilde{Y} = Y_1(x_L)-iY_0(x_L) $ et $ \widetilde{J}=J_1(x_L)+iJ_0(x_L) $ : $ \phi(x) = \frac{J_0(x)*\widetilde{Y} + Y_0(x)*\widetilde{J}}{J_0(x_0)*\widetilde{Y}+Y_0(x_0)*\widetilde{J}} $
N.B. La pente du fond n'est pas représentée ici.
[modifier] Solution semi-analytique (homotopie)
On a donc $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $ avec $ H=-ax+h $
D'où $ (-ax+h)\phi_{xx}(x)-a\phi_x(x)+k^2(-ax+h)\phi(x)=0 $
On a donc la relation d'homotopie :
$ (1-p)(\phi_{xx}-u_{0,xx})+p((h-ax)\phi_{xx}-a\phi_x(x)+k^2(h-ax)\phi(x)=0 $
On prend $ u_0=0 $ pour simplifier les calculs. On obtient donc :
$ (1-p)(\phi_{xx}+p((h-ax)\phi{xx}-a\phi_x(x)+k^2(h-ax)\phi(x)=0 $
Ordre 0 :
- $ \phi_{0,xx}=0 \Rightarrow \dfrac{\partial ϕ_0}{\partial x} = A \Rightarrow \phi_0=Ax+B $
- $ \phi_0(0)=B=1 \Rightarrow B=1 \Rightarrow \phi_0=Ax+B $
- $ \dfrac{\partial ϕ_0}{\partial x}(L) = ik(AL+B)=A \Rightarrow ik(AL+1)=A \Rightarrow A=\dfrac{ik}{1-ikL} $
D'où : $ \boxed{\phi_0(x)=\dfrac{ikx}{1-ikL}x+1} $
Ordre 1 :
- $ \phi_{1,xx}+(h-ax-1)\phi{0,xx}-a\phi_{0,x}+k^2\phi_0=0 $
- $ \dfrac{\partial ϕ_1^2}{\partial x^2}= -(h-ax-1)\dfrac{\partial ϕ_0^2}{\partial x^2}+a\dfrac{\partial ϕ_0}{\partial x}-k^2\phi_0 $
- $ \dfrac{\partial ϕ_1}{\partial x}= -(h-ax-1)\dfrac{\partial ϕ_0}{\partial x}+a ϕ_0-\int{k^2}\phi_0+A $
- $ ϕ_1= -(h-ax-1)ϕ_0+a \int{ϕ_0}-k^2\iint{\phi_0}+Ax+B $
or $ ϕ_0=\dfrac{ikx}{1-ikL}x+1 ~ie~ \int{ϕ_0}=\dfrac{ikx^2}{2(1-ikL)}x^2+x ~ie~ \iint{ϕ_0}=\dfrac{ikx^3}{6(1-ikL)}x^3+\dfrac{x^2}{2} $
D'où : $ \boxed{\phi_1(x)=(ax+1-h)\phi_0+a(\dfrac{ikx^2}{2(1-ikL)}x^2+x)-k^2(\dfrac{ikx^3}{6(1-ikL)}x^3+\dfrac{x^2}{2})+Ax+B} $
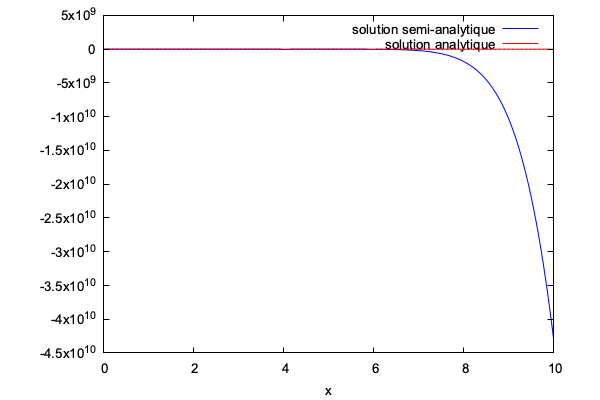
Les graphes donnés par Maxima sont déconcertants (pour l'instant):
Graphe avec prise en compte du module de $ \phi $ La solution homotopique n'est même pas calculée.
Graphe sans prise en compte du module de $ \phi $
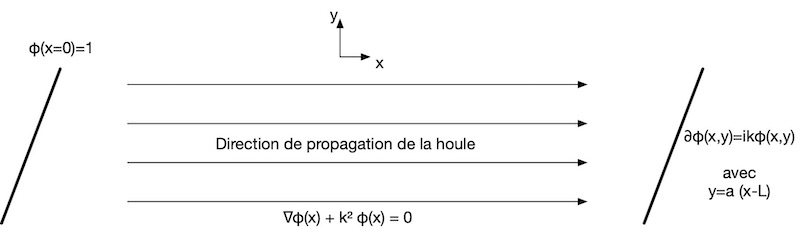
[modifier] Cas n°5 : domaine bidimensionnel plat avec direction préférentielle des houles
Le dernier cas concret que nous traitons est un domaine bidimensionnel plat avec une direction préférentielle des houles.
L'équation de Berkhoff se simplifie comme suivant pour un canal bidimensionnel :
$ \nabla (gH\nabla\phi)+k^2gH\phi=0 $
Dans ce cas précis, le fond est plat, d'où : $ \nabla \phi+k^2\phi=0 $
Ici, on ne peut pas trouver la solution analytique. On peut seulement approcher la solution grâce à une méthode de différences finies ou grâce à l'homotopie. Nous allons ici résoudre cette équation par homotopie (solution semi-analytique).
[modifier] Solution semi-analytique (homotopie)
On a $ \nabla \phi(x,y)+k^2\phi(x,y)=0 ~ie~ \dfrac{\partial^2\phi}{\partial x^2}+\dfrac{\partial^2\phi}{\partial y^2}+k^2\phi(x,y)=0 $
Donc on obtient la relation homotopique suivante : $ (1-p)(\phi_{xx}+\phi_{yy})+p(\phi_{xx}+\phi_{yy}+k^2\phi)=0 $
Une idée de développement peut être de considérer l'équation de Berkhoff, simplifiée en Helmholtz :
Et de faire un changement de repère de façon à obtenir :
[modifier] Les limites du modèle et applications
Nous rencontrons 2 grands types de limitations : les limitations physiques ainsi que les limitations mathématiques
[modifier] Limites physiques
- Le fond du canal influence la houle et réciproquement. Or, notre modèle ne prend notamment pas en compte des phénomènes tels que le transport des sédiments et du sable qui pourraient modifier le fond du canal et donc avoir une influence sur la houle. Ces phénomènes sont cependant limités car se déroulant sur un temps long.
- Le fond est en général très irrégulier, et la présence de hauts-fonds ou d'autres irrégularités est de nature à modifier la houle ; c'est d'ailleurs ce qui est en général utilisé pour limiter l'érosion, en installant des épaves de bateau en guise de digue par exemple.
 (Épaves protectrices - Moreton Island, Australie - Photo Ludovic BRETON - travail personnel)
(Épaves protectrices - Moreton Island, Australie - Photo Ludovic BRETON - travail personnel)
- Le trait de côte est très irrégulier lui aussi, et les phénomènes de réflexion et diffraction sont nombreux. Modéliser la houle en simplifiant le trait de côte peut ainsi induire des erreurs.
- L'onde est assimilée à une onde sinusoïdale pure. Bien que la houle a tendance à devenir une onde pure au bout d'une certaine distance (en ne conservant que les ondes les plus longues), celle-ci n'est pas forcément totalement pure, et notre modèle ne le prend pas en compte.
- Nous pouvons questionner le réalisme de certaines données (kL = 1 par exemple).
- Les vagues deviennent de la houle à partir du moment où elles quittent leur aire génératrice (en général loin au large), c'est-à-dire où elles sortent de la zone où souffle le vent qui les a fait naître. Il y a donc très souvent une différence entre "vagues de mer" et houle au niveau de leurs direction, célérité et amplitude. Ce modèle n'est pas capable de prendre en compte des zones où la mer est fréquemment sujette à des "croisements" entre vagues et houle.

Enfin, considérer la hauteur d'eau comme un proxy pour la quantification de l'érosion est réducteur, puisque seule l'énergie potentielle des vagues est considérée. Leur énergie cinétique n'est pas prise en compte ; or on peut raisonnablement penser que celle-ci joue fortement sur l'érosion du trait de côte, ainsi que sur les submersions marines.
[modifier] Limites mathématiques
- Beaucoup de variables sont considérées constantes ($ k,\omega,L $etc), afin de limiter la complexité du modèle.
- on suppose une uniformité spatiale et temporelle du phénomène : La zone génératrice de la houle est supposée être à un seul endroit et constante. On peut ainsi prédire l'effet d'une houle moyenne (en ondes longues, donc à faible profondeur), mais le pouvoir érosif de grandes crêtes n'est pas calculé.
- l'ordre d'homotopie "n" influe beaucoup sur la qualité du modèle : La divergence est rapide si "n" est petit.
[modifier] Propositions d'applications
Cette méthode permet de modéliser à la fois la réflexion des ondes, ainsi que leur réfraction ou diffraction sur les digues.
Elle permet ainsi de prédire non seulement les phénomènes de submersion marine, mais aussi et surtout l’impact de l’érosion sur le trait de côte.
De plus, la méthode de l'homotopie méthode s’adapte à une grande variété de géométries et donc une grande variété de cas.
Cela peut être très utile pour modéliser des formes de littoral complexes avec des estuaires, des rades ou des baies par exemple afin de piloter leur aménagement par la suite.
 S'abonner à un flux RSS
S'abonner à un flux RSS