Utilisateur:ABET / CASTELLAN / KERGOAT : Différence entre versions
| Ligne 35 : | Ligne 35 : | ||
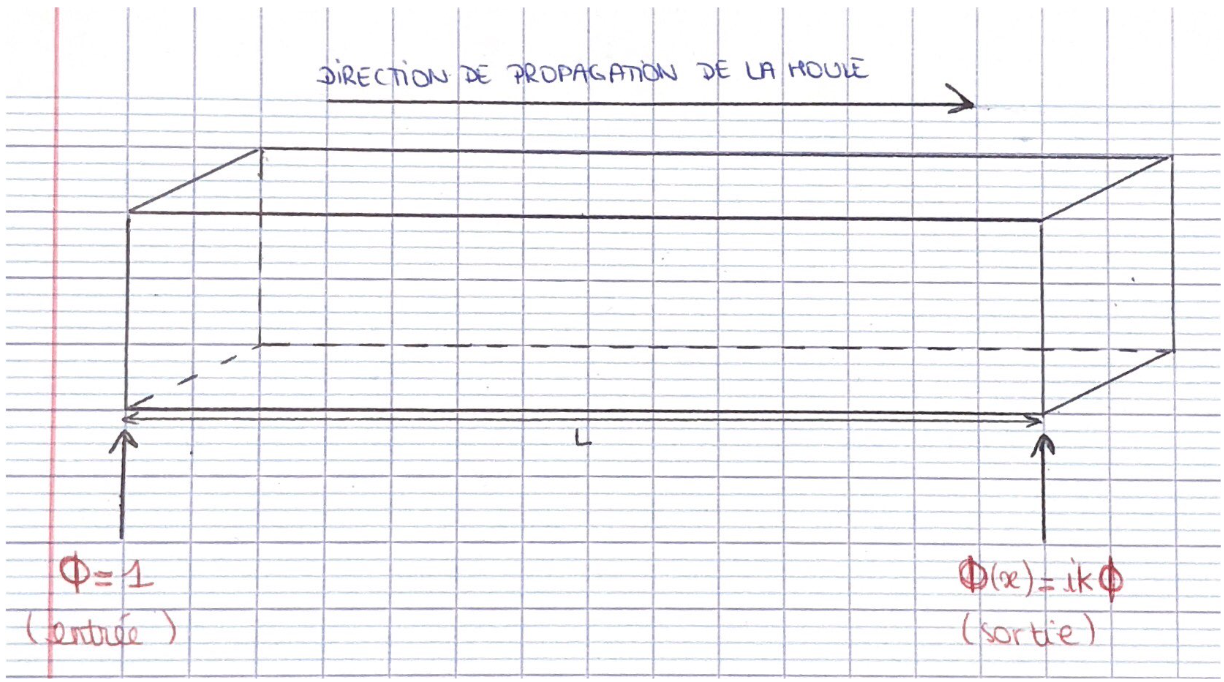
On se place dans le cas d’un canal monodimensionnel plat de longueur L avec une fréquence d’entrée au niveau de l’aval φ = 1 et une sortie libre au niveau de l’amont avec <math>\phi_{x} = ik\phi </math> | On se place dans le cas d’un canal monodimensionnel plat de longueur L avec une fréquence d’entrée au niveau de l’aval φ = 1 et une sortie libre au niveau de l’amont avec <math>\phi_{x} = ik\phi </math> | ||
| + | |||
| + | [[File:Cas_1_Model.png]] | ||
==== <span style="color:seagreen">Résolution Analytique</span> ==== | ==== <span style="color:seagreen">Résolution Analytique</span> ==== | ||
Version du 6 juin 2023 à 10:31
Sommaire |
IMPACT DU CHANGEMENT CLIMATIQUE SUR LES CÔTES ET DANS LES ESTUAIRES
Contexte
”Environ 1 milliard de personnes pourraient vivre d’ici 2050 dans des zones côtières menacées par la montée des eaux et les épisodes de submersions marines lors des tempêtes” , alertent les experts de l’ONU.
C’est dans ce climat d’incertitude et d’insécurité qu’évoluent les populations côtières, c’est à dire plus de 60 pourcents de la population mondiale. L’érosion des côtes et l’impact de la houle sur les littoraux s’accélèrent avec le changement climatique. Ce phénomène doit donc être étudié afin d’anticiper l’érosion des littoraux et de réaliser des aménagements adaptés. C’est pourquoi des outils mathématiques sont nécessaires pour prévoir l’impact des houles sur le littoral.
C’est en appliquant le principe de l’homotopie à l'équation de Berkhoff que nous pouvons modéliser l’impact du réchauffement climatique et de la houle sur les côtes.
- le bâtiment Le Signal, un symbole de l’érosion côtière en France (Gironde), d’après Le Monde.
Méthode homotopique
L’objectif de l’homotopie est de résoudre des équations différentielles et des intégrales. A partir d’une solution connue relativement simple, elle permet de converger vers une solution plus complète grâce à un paramètre p qui varie entre 0 et 1. Il assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre.
Elle est définie comme suit :$ (1−p)[L(U(x,t);p)−L(u0(x,t))]+cH(p)[L(U(x,t);p)−N(U(x,t),p)−f(x)] $
avec L est un opérateur linéaire, N un opérateur non-linéaire, f les termes complémentaires de l’équation et u0 est une estimation initiale de la solution.
Dans notre cas, on prendra $ H(p)=p $
Etude des différents cas
Cas n°1
On se place dans le cas d’un canal monodimensionnel plat de longueur L avec une fréquence d’entrée au niveau de l’aval φ = 1 et une sortie libre au niveau de l’amont avec $ \phi_{x} = ik\phi $
Résolution Analytique
On souhaite résoudre l’équation du modèle de Berkhoff $ \boxed{\nabla.(CC_{g}\nabla\phi) + k^2\phi = 0} $
On pose une solution du potentiel $ \phi = A\mathrm{e}^{ikx} + B\mathrm{e}^{-ikx} $ et on résoud l’équation à l’aide des conditions aux limites
- Condition 1 :
$ \phi(x=0)=1 $
$ \phi(x=0) = A + B = 1 \Rightarrow A = 1 - B $
- Condition 2 :
$ \phi_x(L) = ik\phi(L) $
$ \phi_x(L) = ikA\mathrm{e}^{ikL} - ikB\mathrm{e}^{-ikL} = ik(A\mathrm{e}^{ikL} + B\mathrm{e}^{-ikL}) $
Il vient: $ 2ikB\mathrm{e}^{-ikL} \Rightarrow B = 0 \Rightarrow A = 1 $
Finalement
$ \phi(x)={e}^{ikx} = cos(kx) + isin(kx) $
Ce qui nous donne:
$ \boxed{h(x,t) = Re(\phi(x))\times{e}^{-i \omega t} = cos(kx)cos(\omega t) - sin(kx) cos(\omega t) =cos(kx-\omega t)} $
Résolution par homotopie
On reprend les mêmes conditions initiales mais cette fois ci on part de la relation d’homotopie $ \boxed{(1-p) \phi_{xx} + p(\phi_{xx}+k^2\phi) = 0} $
On introduit la décomposition de φ telle que:
$ \phi(x,p) = \phi_0(x) + p\phi_1(x) + p^2\phi_3(x) + p^3\phi_3(x) + ... $
$ \phi_{xx}(x) = \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... $
L’équation générale d’homotopie avec la décomposition s’écrit donc
$ \boxed{(1-p)(\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ...) + p ( \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... + k^2 + \phi_0(x) + p\phi_1(x) + p^2\phi_3(x) + p^3\phi_3(x) + ... ) = 0} $
- Ordre 0
On reprend l’équation à l’ordre 0 telle que:
$ (1-p)\phi_{0,xx} + p\phi_{0,xx} = 0 \Rightarrow \phi_{0,xx} = 0 \Rightarrow \phi_0 = Ax + B $
Conditions aux limites
$ \begin{cases} \phi_0^0 = 1 = B \\\phi_{0,x}^L = ik\phi_{0}^L = ik(AL + 1) = A \Rightarrow A = \frac{ik}{1-ikL} \end{cases} $
On a donc
$ \phi_0 (x) = \frac{ik}{1-ikL} x + 1 $
- Ordre 1
On reprend l’équation à l’ordre 1 telle que:
$ (1-p)(\phi_{0,xx} + p\phi_{1,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + k^2\phi_0) = 0 $
On a vu à l’ordre 0 que $ \phi_{0,xx} = 0 donc \phi_{1,xx} = -k^2\phi_0 \Rightarrow \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B $
Conditions aux limites $ \begin{cases} \phi_1^0 = 0 = B \\\ phi_{1,x}^L = ik \phi_1^L \end{cases} $
On obtient après calculs $ \boxed{\phi_1(x) = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} x - k^2(\frac{ik}{6-ikL} x^3 + \frac{1}{2} x^2)} $
- Ordre 2
Pour simplifier l'écriture on pose $ \alpha = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} $ et $ \beta = \frac{ik}{6-ikL} $
On reprend l'équation générale à l'ordre 2 telle que $ (1 - p)(\phi_{0,xx} + p\phi_{1,xx} + p^2\phi_{2,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + p^2\phi_{2,xx} + k^2\phi_0 + k^2p\phi_1 = 0 $
Sachant que $ \phi_{1,xx} = - k^2\phi_0 $ et $ \phi_{0,xx} = 0 $, on obtient :
$ p(-k^2\phi_0 + p^2\phi_{2,xx}) + pk^2\phi_0 + p^2k^2\phi_1 = 0 \Rightarrow \phi_{2,xx} = - k^2\phi_1 \Rightarrow \phi_2 = -k^2 \int\int\phi_1dxdx + Ax + B $
Conditions aux limites
$ \begin{cases} \phi_2^0 = B \\ \phi_{2,x}^L = ik\phi_2^L \\ \phi_{2,x}^L = ik[-k^2\int\int(\alpha x - k^2(\beta x^3 + \frac{1}{2} x^2)) dx dx +AL] = ik [-k^2(\alpha\frac{1}{6} L^3 - k^2 ( \beta \frac{1}{20} L^5 + \frac{1}{24} L^4 + AL)] \\ \phi_{2,x}^L = -k^2[\alpha \frac{1}{2} L^2 - k^2 ( \beta \frac{1}{4} L^4 + \frac{1}{6} L^3)] + A\\ \ A = \frac{ik}{1-ikL}[-k^2(\frac{1}{6}\alpha L^3 - k^2(\frac{1}{20}\beta L^5 + \frac{1}{24} L^4) - \frac{1}{2}\alpha L^2 + k^2(\frac{1}{4}\beta L^4 + \frac{1}{6} L^3)] \end{cases} $
$ \boxed{\phi_2 = -k^2 [ \frac{1}{6}\alpha x^3 - k^2(\frac{1}{20}\beta x^5 + \frac{1}{24} x^4)] + Ax} $
Cas n°2
On se place dans le cas d’un domaine monodimensionnel plat de longueur L avec entrée par l’aval d’une onde de fréquence unitaire et une condition de flux aval $ \phi_x=ik(2-\phi) $ et réflexion totale amont $ \phi_x=0 $.
Résolution Analytique
Comme dans le cas n°1: On obtient $ \phi = A\mathrm{e}^{ikx} + B\mathrm{e}^{-ikx} $et on résout l’équation à l’aide des conditions aux limites:
- En aval:
$ \phi(x=0) = ik(2-\phi) $ ce qui nous donne $ \phi_x (0) = ikA-ikB=ik(2-A-B) \Rightarrow A=1 $
- En amont:
$ \phi_{x}(x=L) = 0 $ ce qui nous donne $ \phi_x (L) = ikA\mathrm{e}^{ikL} - ikB\mathrm{e}^{-ikL} = 0 \Rightarrow B = \mathrm{e}^{2ikL} $
Finalement
$ \boxed{\phi(x) = \mathrm{e}^{ikL} - \mathrm{e}^{ik(2L-x)}} $
Résolution par homotopie
- Ordre 0
On a $ \phi_0(x) = Ax+B $ Ce qui nous donne $ \phi_{0,x}^0 = A =ik(2-B) $ et $ \phi_{0,x}^L = A = 0 $
Donc $ B = 2 \Rightarrow <span style="color:crimson">\boxed{ \phi_0 = 2} $</span>
- Ordre 1
En partant de la relation d'homotopie on obtient comme pour le premier cas :
$ \phi_{1,xx} + k^2\phi_0 = 0 $ donc $ \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B $
Soit $ \boxed{\phi_{1} = -k^2x^2 + Ax + B et <math>\phi_{1,x} = -2xk^2 + A} $
Conditions aux limites $ \begin{cases} \phi_{1,x}^0 = ik(2 - \phi_1^0) = ik(2 - B) = A \Rightarrow B = 2 - \frac{A}{ik}\\ \phi_{1,x}^L = 0 = -2Lk^2 + A \Rightarrow A = 2Lk^2 \end{cases} $
Donc B = 2(1 + iLk)
Au final $ \phi_1 = - k^2x^2 + 2xLk^2 + 2(1 + ikL) $
- Ordre 2
Ici $ \phi_{2,xx} + k^2\phi_0 = 0 \Rightarrow \phi_2 = -k^2\int\int\phi_{0}dxdx +Ax + B = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + Ax + B $ $ \phi_{2,x} = -k^2\int\phi{1}dx + A = -k^2 ( -k^2\frac{x^3}{3} + Lk^2\frac{x^2}{3} + 2ikLx ) + A $
Conditions aux limites $ \begin{cases} \phi{2,x}^0 = A = ik(2 - \phi^0) = ik ( 2 - B ) \Rightarrow B = 2 - \frac{A}{ik}\\ \phi{2,x}^L = 0 \Rightarrow A = -k^2 ( -k^2\frac{L^3}{3} + k^2\frac{L^3}{3} + 2ikL^2 ) \Rightarrow A = -2ik^{2}L^2 \end{cases} $
Donc B = 2 ( 1 - kL^2 )
Au final, on a $ \boxed{\phi_2 = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + -2ik^{2}L^{2}x + B = 2 ( 1 - kL^2 )} $
Cas n°3
On se place dans le cas d’un canal monodimensionnel de longueur L avec une pente de fond constante (s=constante) avec entrée par l’aval d’une onde de fréquence $ \phi = 1 $ et sortie libre en amont $ \phi_{x} = ik\phi $
Résolution Analytique
On part de l’équation de Berkhoff en considérant qu’on se trouve en petite profondeur soit $ \nabla.(CC_{g}\nabla\phi) + k^2\phi = 0 $ avec $ C = C_{g} =\sqrt{gH} $ non constantes
- Cas 1 $ k = k_{0}\sqrt\frac{H_{0}}{H(x)} $
$ \nabla.(gH\nabla\phi) = gH \frac{\partial^2\phi}{\partial^2x} - g\frac{\partial{H}}{\partial{x}} \frac{\partial\phi}{\partial{x}} $
On injecte dans l’équation de Berkhoff, on divise l’équation par g et on pose le changement de variable $ H(x) = z = H_0 - sx \Rightarrow \frac{\partial{H}}{\partial{x}} = -s \frac{\partial{H}}{\partial{z}} $ pour obtenir $ H \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k^{2}H\phi = 0 $
En prenant en compte la condition sur k, on obtient $ (H_{0} - sx) \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k_{0}^{2}H_{0}\phi = 0 $
On note que $ \frac{\partial\phi}{\partial{x}} = - s \frac{\partial\phi}{\partial{z}} et \frac{\partial^2\phi}{\partial^2{x}} = s_{2} \frac{\partial^2\phi}{\partial^2{z}} $
Soit en multipliant par $ z $ et en divisant par $ s^2 $ l’équation devient $ z_{2}\frac{\partial^2\phi}{\partial^2{z}} + z\frac{\partial\phi}{\partial{z}} + \frac{k_{0}^{2}}{s^{2}}zH_{0}\phi $ que l’on peut associer à une équation de Bessel, il faut poser $ \alpha^{2} = \frac{k_{0}^{2} H_{0}}{s^2} $ on obtient $ z^{2}\phi_{zz} + z\phi_z + \alpha^{2}z\phi = 0 $
On pose $ A $ et $ B $ deux constantes et $ J_0 $ et $ Y_0 $ des fonction de Bessel respectivement de première et de deuxième espèce d’ordre 0. On pose alors la solution $ \phi(z) = A J_{0}(2\alpha\sqrt{z}) + B Y_{0}(2\alpha\sqrt{z}) $
$ \begin{cases} \phi(x=0) = \phi(z=H_{0}) = AJ_{0}(2\alpha\sqrt{H_{0}}) + BY_{0}(2\alpha\sqrt{H_{0}}) = 1\\ \Rightarrow \\ A = \frac{1 - BY_{0}(2\alpha\sqrt{H_{0}})}{J_{0}(2\alpha\sqrt{H_{0}})} \\ \phi_{x}{x=L} = -s \phi_{z}(z=H_{0}-sL=z_{L}) = ik\phi(z=H_{0}-sL) \Rightarrow \phi_z^{z_{L}} = \frac{ik}{s} (AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}}) = \frac{\alpha}{\sqrt{z_{L}}} AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}}) \Rightarrow i((AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}})) = AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}}) \\ \Rightarrow B = A\frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}}{iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}} \end{cases} $
On trouve alors $ A = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} $ et $ B = \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}}(J_{1}(2\alpha\sqrt{z_{L}} - iJ_{0}(2\alpha\sqrt{z_{L}}))} $
Finalement
$ \boxed{\phi = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})} J_{0}(2\alpha\sqrt{z}) + \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}}(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}}(J_{1}(2\alpha\sqrt{z_{L}} - iJ_{0}(2\alpha\sqrt{z_{L}})} Y_{0}(2\alpha\sqrt{z})} $
Résolution par homotopie
On prend l'équation générale d'homotopie adapté au changement de variable telle que : $ (H_{0} - sx) \phi_{xx} - s\phi_{x} + k_{0}^{2}H_{0}\phi = 0 $
- Ordre 0
A l'ordre 0, on a $ \phi_{0,xx} = 0 $ soit $ \phi_{0} = Ax + B $
D'après les conditions initiales on a :
$ \begin{cases} \phi(x=0) = 1 = B\\ \phi_{x}(x=L) = ik\phi(x=L) \end{cases} $
On retrouve la même solution que pour l'ordre 0 du cas 1 tel que $ \boxed{\phi_{0}(x) = \frac{ik}{1-ikL} x + 1} $
- Ordre 1
Tout comme dans les autre cas on a $ \phi_{0,xx} = 0 $ donc après calculs sur l’équation d’homotopie, on obtient $ \boxed{\phi_{1,xx} + (H_{0} - sx)\phi_{0,xx} - s\phi{0,x} + k_{0}^2H_{0}\phi_{0} = 0} $
Soit $ \phi_{1,xx} = s\phi_{0,x} - k^2H_{0}\phi_{0} = -s(\frac{ik}{1-ikL} - k^{2}H_{0}(\frac{ik}{1-ikL}x + 1) $ $ \phi_{1,x} = -s(\frac{ik}{1-ikL}x - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}x^{2} + x) + A $ $ \phi_{1} = -s(\frac{ik}{2(1-ikL)}x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + Ax + B $
Conditions initiales
- $ \phi_{1}^{0} = 1 = B $ - $ \phi{1,x}^{L} = s(\frac{ik}{1-ikL}L - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}L^{2} + L) + A = ik (-s(\frac{ik}{2(1-ikL)}L^{2} - k^{2}H_{0}(\frac{ik}{6(1-ikL)}L^{3} + \frac{L^{2}}{2}) + AL + 1) $
En posant $ \alpha = \frac{ik}{1 - ikL} $ on obtient
$ s(\alphaL - k^{2}H_{0}(\frac{\alpha}{2}L^{2} + L) + A = ik (-s(\frac{\alpha}{2(}L^{2} - k^{2}H_{0}(\frac{\alpha}{6}L^{3} + \frac{L^{2}}{2}) + AL + 1) $
Soit $ A(1 - ikL) = s(\alpha(L - ik\frac{L^{2}}{2}) - k_{0}^{2}H_{0}(-\frac{\alpha}{2}L^{2} - L + ik\frac{\alpha}{6}L^{3} +ik\frac{L^{2}}{2}) + ik $
En divisant et en remplaçant $ \alpha $ par son expression, on trouve : $ A = \frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}}) - \frac{(ik)^2k_{0}^2H_{0}L^{2}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) = \frac{ik}{1 - ikL} $
Au final $ \phi_{1}(x) = -s(\frac{ik}{2(1-ikL)}x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + (\frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}}) - \frac{(ik)^2k_{0}^2H_{0}L^{2}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) = \frac{ik}{1 - ikL}) x + 1 $
Cas n°4
On s'intéresse ici à une vague générée par une source périodique sinusoïdale. On se place en grande profondeur, une source ponctuelle est placée autour d'un cercle de rayon $ r_0 $, le cercle est lui-même centré sur un domaine circulaire de rayon R. L'équation de Berkhoff s'exprime alors $ \Delta\phi = k^2\phi = 0 $
Avec les conditions initiales suivantes $ \begin{cases} \phi^{r=r_{0}} = 1\\ \phi_{r}^{r=R} = ik\phi^{r=R} \end{cases} $
Le problème étant caractérisé par une symétrie de révolution, l'équation se transforme telle que : $ \phi_{rr} = \frac{1}{r}\phi_{r} + k^2\phi = 0 $
On prendra les valeurs numériques suivantes $ R_{0} = 1m, R = 100m $ et $ k = 0.1m^{-1} $
Résolution Analytique
On retrouve une équation du type Bessel traitée dans le cas 3, la solution est du type $ \phi(r) = AJ_{0}^{kr} + BY_{0}^{kr} \Rightarrow \phi_{r}^{r} = k(AJ_{1}^{kr} + BY_{1}^{kr}) $
En prenant, les conditions initiales : $ \begin{cases} \phi^{r=r_{0}} = AJ_{0}^{kr_{0}} + BY_{0}^{kr_{0}} = 1\\ \phi_{r}^{r=R} = -(kAJ_{1}^{kR} + kBY_{1}^{kR}) = ikAJ_{0}^{kR} + ikBY_{0}^{kR} \end{cases} $
On retrouve de la même manière que pour le cas 3 $ B = \frac{1-AJ_{0}^{kr_{0}}}{Y_{0}^{kr_{0}}} $ et $ A = -B\frac{ikY_{0}^{kR} + kY_{1}^{kR}}{ikJ_{0}^{kR} + kJ_{1}^{kR}} $
Après calcul on obtient $ B = \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR})}} $ et $ A = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR})}} $
Soit
$ \boxed{\phi(r) = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR})}}J_{0}^{kr} + \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR})}}Y_{0}^{kr}} $
Résolution par homotopie
On part de l’équation d’homotopie suivante $ (1-p)\phi_{rr} + p\phi_{rr} + \frac{1}{r}\phi_{r} + k^2\phi = 0 $
- Ordre 0
On reprend les mêmes conditions que précédemment telles que $ \phi_{0,rr} = 0 $ ce qui implique $ \phi_{0} = Ar + B $
Conditions aux limites : $ \begin{cases} \phi^{r_{0}} = 1 = Ar{0} + B\\ \phi_{r}^{R} = A = ik(AR + B) \Rightarrow \ A = \frac{ik}{1 - ikR}B \end{cases} $
Après résolution, on obtient $ B = \frac{1 - ikR}{1 + ik(r_{0} - R)} $ et $ A = \frac{ik}{1 + ik(r_{0} - R)} $
Au final pour l’ordre 0 $ \boxed{\phi_{0} = \frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}} $
- Ordre 1
On reprend l’équation générale d’homotopie pour un ordre 1, on trouve $ \phi_{1,rr} + \frac{1}{r} \phi_{0,r} + k^2\phi_{0} = 0 $
Soit $ \phi_{1,rr} = - \frac{1}{r} (\frac{ik}{1 + ik(r_{0} - R)}) - k^2 (\frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}) $
$ \Rightarrow \phi_{1,r} = -ln(r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} r^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} r + C_{1} $
$ \Rightarrow \phi_{1} = - (r ln(r) - r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r^2 + C_{1}r + C_{2} $
Conditions aux limites : $ \begin{cases} \phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r_{0}^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} R^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} R + C_{1} = ik ( - (R ln(R) - R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} R^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} R^2 + C_{1}R + C_{2} \end{cases} $
En reprenant les notations à l'ordre à pour $ A $ et $ B $, on a
$ \begin{cases}\phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) A - \frac{k^2}{6} A r_{0}^3 - \frac{k^2}{2} B r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) A - \frac{k^2}{2} A R^2 - k^2 B R + C_{1} = ik ( - (R ln(R) - R) A - \frac{k^2}{6} A R^3 - \frac{k^2}{2}B R^2 + C_{1}R + C_{2} \end{cases} $
 S'abonner à un flux RSS
S'abonner à un flux RSS