Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/Emeline/Jallet : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
| − | == Modèle de Berkhoff == | + | == '''Modèle de Berkhoff''' == |
La houle peut être modélisée par l'équation aux dérivées partielles (EDP) issue du modèle de Berkhoff suivante : | La houle peut être modélisée par l'équation aux dérivées partielles (EDP) issue du modèle de Berkhoff suivante : | ||
| Ligne 9 : | Ligne 9 : | ||
<math> \phi </math> : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence <math>\omega </math>, C : la célérité de l’onde, Cg : la célérité de groupe des vagues. | <math> \phi </math> : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence <math>\omega </math>, C : la célérité de l’onde, Cg : la célérité de groupe des vagues. | ||
| − | == | + | == '''Résolution''' == |
Pour résoudre cette équation, nous utiliserons une méthode analytique lorsque cela sera possible et une méthode par homotopie. | Pour résoudre cette équation, nous utiliserons une méthode analytique lorsque cela sera possible et une méthode par homotopie. | ||
Nous nous placerons dans différent cas pour résoudre cette équation. | Nous nous placerons dans différent cas pour résoudre cette équation. | ||
| − | === Cas N°1 === | + | === '''Cas N°1''' === |
Pour ce premier cas, nous étudierons le cas d'un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire <math>\phi=1</math>(condition de Dirichlet) et sortie libre amont <math>\phi_{x}=ik\phi</math> (condition de Robin). | Pour ce premier cas, nous étudierons le cas d'un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire <math>\phi=1</math>(condition de Dirichlet) et sortie libre amont <math>\phi_{x}=ik\phi</math> (condition de Robin). | ||
| − | + | ==== Méthode analytique ===== | |
Dans cette situation l'équation issue du modèle de Berkhoff s'écrit : <math> \phi_{xx} + k^2\phi=0 </math>. | Dans cette situation l'équation issue du modèle de Berkhoff s'écrit : <math> \phi_{xx} + k^2\phi=0 </math>. | ||
| Ligne 40 : | Ligne 40 : | ||
| − | + | ==== Méthode par homotopie ==== | |
En choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle, la relation d'homotopie devient : | En choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle, la relation d'homotopie devient : | ||
| Ligne 56 : | Ligne 56 : | ||
<math> (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0</math> | <math> (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0</math> | ||
| − | Ordre 0 | + | ===== Ordre 0 ===== |
| + | A l'ordre 0, on a: | ||
<math> \phi_{xx}=0 </math> | <math> \phi_{xx}=0 </math> | ||
donc | donc | ||
| Ligne 79 : | Ligne 80 : | ||
| − | Ordre 1 | + | ===== Ordre 1 ===== |
| + | Puis à l'ordre 1: | ||
<math> \phi_{1,xx}(x)={-k^2}\phi_0(x) </math> | <math> \phi_{1,xx}(x)={-k^2}\phi_0(x) </math> | ||
| Ligne 114 : | Ligne 116 : | ||
| − | Ordre 2 | + | ===== Ordre 2 ===== |
| + | On peut ensuite modéliser les ordres suivants grâce à WXMaxima | ||
A partir des valeurs numériques suivantes : | A partir des valeurs numériques suivantes : | ||
| Ligne 130 : | Ligne 133 : | ||
[[File:Gif cas 1.gif | 400px]] | [[File:Gif cas 1.gif | 400px]] | ||
| − | + | ==== Etude de sensibilité ==== | |
| + | On regarde la convergence de la méthode par homotopie en fonction du produit kL. | ||
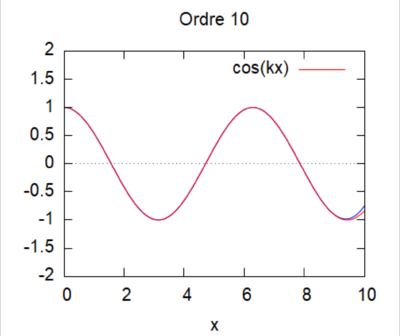
Cas kL=0,25 [[File: cas 1 ordre 10 kL = 0,25.png|400px]] | Cas kL=0,25 [[File: cas 1 ordre 10 kL = 0,25.png|400px]] | ||
| Ligne 138 : | Ligne 142 : | ||
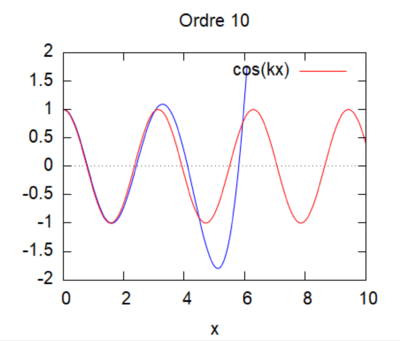
Cas kL=2 [[File:cas 1 ordre 10 kL = 2.png|400px]] | Cas kL=2 [[File:cas 1 ordre 10 kL = 2.png|400px]] | ||
| − | === Cas N°2 === | + | === '''Cas N°2''' === |
Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval <math> \phi_{x} =ik(2−\phi) </math> et réflexion totale amont <math> \phi_{x}=0 </math>. | Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval <math> \phi_{x} =ik(2−\phi) </math> et réflexion totale amont <math> \phi_{x}=0 </math>. | ||
| − | + | ==== Méthode analytique ==== | |
Comme pour le cas N°1, l'équation de Berkhoff à une dimension s'écrit <math> \phi_{xx} + k^2\phi = 0 </math> | Comme pour le cas N°1, l'équation de Berkhoff à une dimension s'écrit <math> \phi_{xx} + k^2\phi = 0 </math> | ||
| Ligne 159 : | Ligne 163 : | ||
La solution réelle associée à cette fonction est <math> h(x) = cos(kx) + cos(2kL+kx) </math> | La solution réelle associée à cette fonction est <math> h(x) = cos(kx) + cos(2kL+kx) </math> | ||
| − | + | ==== Méthode par homotopie ==== | |
En procédant de la même manière que dans le cas 1 on retrouve comme relation d'homotopie : | En procédant de la même manière que dans le cas 1 on retrouve comme relation d'homotopie : | ||
| Ligne 165 : | Ligne 169 : | ||
<math> (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 </math> | <math> (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 </math> | ||
| − | Ordre 0 : | + | ===== Ordre 0 ===== |
| + | |||
| + | Tout d'abord, à l'ordre 0: | ||
<math> \phi_{0,xx}(x)=0 </math> | <math> \phi_{0,xx}(x)=0 </math> | ||
| Ligne 184 : | Ligne 190 : | ||
Donc <math> \phi_0(x)=2 </math> | Donc <math> \phi_0(x)=2 </math> | ||
| − | Ordre 1 : | + | ===== Ordre 1 ===== |
| + | |||
| + | Ensuite, pour l'ordre 1: | ||
On a <math> \phi_{1,xx}(x) = -k^{2}\phi_0(x) </math> | On a <math> \phi_{1,xx}(x) = -k^{2}\phi_0(x) </math> | ||
| Ligne 198 : | Ligne 206 : | ||
[[File:Gif cas 2 Thomas et Emeline.gif|400px]] | [[File:Gif cas 2 Thomas et Emeline.gif|400px]] | ||
| − | + | ==== Etude de sensibilité ==== | |
| − | === Cas N°3 === | + | === '''Cas N°3''' === |
Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec une pente de fond constante (s=cst). L'entrée se fait par l'aval avec une onde de fréquence unitaire <math> \phi_{x} =ik(2−\phi) </math> et la sortie en amont <math> \phi_{x}(x=L)=ik\phi(x=L) </math>. | Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec une pente de fond constante (s=cst). L'entrée se fait par l'aval avec une onde de fréquence unitaire <math> \phi_{x} =ik(2−\phi) </math> et la sortie en amont <math> \phi_{x}(x=L)=ik\phi(x=L) </math>. | ||
| + | |||
| + | ==== Résolution analytique ==== | ||
Le problème est complexifié puisque H(x) n'est plus égal à <math>H_0</math> mais à <math>H_0-sx</math>. | Le problème est complexifié puisque H(x) n'est plus égal à <math>H_0</math> mais à <math>H_0-sx</math>. | ||
| Ligne 240 : | Ligne 250 : | ||
| − | + | ==== Résolution par homotopie ==== | |
Soit la relation d'homotopie suivante : <math>(1-p)\phi_{xx}+p(H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0</math> | Soit la relation d'homotopie suivante : <math>(1-p)\phi_{xx}+p(H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0</math> | ||
| Ligne 255 : | Ligne 265 : | ||
[[File:Gif cas 3.gif | 400px]] | [[File:Gif cas 3.gif | 400px]] | ||
| − | === Cas N°4 === | + | === '''Cas N°4''' === |
Dans ce cas nous avons une vague sphérique générée par une source sinusoïdale | Dans ce cas nous avons une vague sphérique générée par une source sinusoïdale | ||
Version du 6 juin 2023 à 17:35
Sommaire |
Modèle de Berkhoff
La houle peut être modélisée par l'équation aux dérivées partielles (EDP) issue du modèle de Berkhoff suivante :
$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $
Avec : $ \phi $ : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence $ \omega $, C : la célérité de l’onde, Cg : la célérité de groupe des vagues.
Résolution
Pour résoudre cette équation, nous utiliserons une méthode analytique lorsque cela sera possible et une méthode par homotopie. Nous nous placerons dans différent cas pour résoudre cette équation.
Cas N°1
Pour ce premier cas, nous étudierons le cas d'un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $(condition de Dirichlet) et sortie libre amont $ \phi_{x}=ik\phi $ (condition de Robin).
Méthode analytique =
Dans cette situation l'équation issue du modèle de Berkhoff s'écrit : $ \phi_{xx} + k^2\phi=0 $.
Soit $ \phi(x) = Ae^{ikx}+Be^{-ikx} $ , A et B sont des constantes à déterminer avec les conditions initiales.
En aval pour x=0, $ \phi=1 $ donc $ A + B = 1 $
En amont pour x = L, $ \phi_{x}(L)=ik\phi{L} $
Donc $ ikAe^{ikL} - ikBe^{-ikL} = ik(Ae^{ikL} + Be^{-ikL}) $.
Ainsi A = 1 et B = 0
La solution analytique de cette équation est donc $ \phi(x)=e^{ikx} $
On s'intéresse à la partie réelle de $ \phi e^{i\omega t} $. Ainsi $ h(x,t) = cos(kx+ \omega t) $
Méthode par homotopie
En choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle, la relation d'homotopie devient :
$ (1-p)\phi_{xx}+ p(\phi_{xx}+k^2\phi)=0 $
Or
$ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+... $
Et $ \phi_{xx}=\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+... $
Donc en injectant ces deux expressions dans la relation d'homotopie on a :
$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $
Ordre 0
A l'ordre 0, on a: $ \phi_{xx}=0 $ donc $ \phi_{0,xx}(x)=0 $
En intégrant deux fois on a :
$ \phi_0(x)=Ax+B $
Avec pour conditions aux limites : $ \phi_0^0=1 $ et $ \phi_{0, x}^L={ik}\phi_0^L $ on a $ B=1 $ et $ A=\frac{ik}{(1-ikL)} $
Détail pour trouver A: $ \phi_{0, x}^L={ik}\phi_0^L $ $ \iff A=\frac{ik}{(AL+1)} $ $ \iff A=\frac{ik}{(1-ikL)} $
Ainsi $ \phi_0(x)=(\frac{ik}{(1-ikL)})x+1 $
Ordre 1
Puis à l'ordre 1: $ \phi_{1,xx}(x)={-k^2}\phi_0(x) $
donc par double intégration on a :
$ \phi_1(x) = -k^2\int\phi_0dxdx +Ax+B $.
Avec pour conditions aux limites :
$ \phi_1^0=0 $ et $ \phi_{1, x}^L={ik}\phi_1^L $
on a $ B=0 $ et $ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $
Calcul de A :
$ \phi_1(x)= -k^2(({ik}/({1-ikL})6)x^3+x^2/2+Ax $
en x=L:
$ \phi_{1, x}^L={ik}\phi_1^L $ $ \iff \frac{ikL^2}{(1-ikL)^2}+L+A=\frac{ik(ikL^3)}{(1-ikL)*6}+\frac{L^2}{2}+AL $
en isolant A dans l'équation on retrouve :
$ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $
On a donc :
$ \phi_{1}(x)= -\frac{k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2}x-k^2(\frac{ik}{6(1-ikL)})x^3+\frac{x^2}{2} $
Ordre 2
On peut ensuite modéliser les ordres suivants grâce à WXMaxima A partir des valeurs numériques suivantes :
$ k=\frac{1}{100} $ (nombre d'onde en m-1)
$ H=40 $ (profondeur en m)
$ c=\sqrt{gH} $ (célérité de l'onde en m/s)
$ \lambda=\frac{2\pi}{k} $ (longueur d'onde en m)
$ L=2\lambda $ (longueur du domaine en m)
Etude de sensibilité
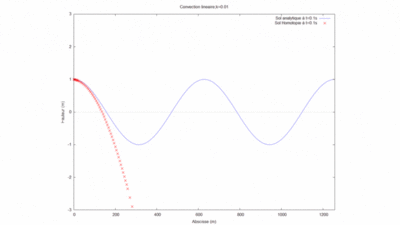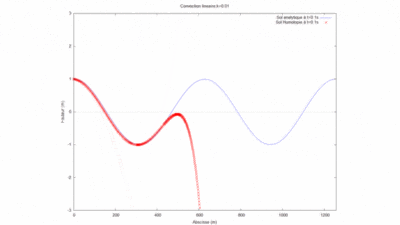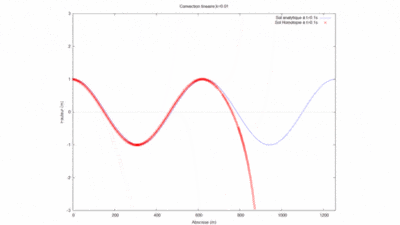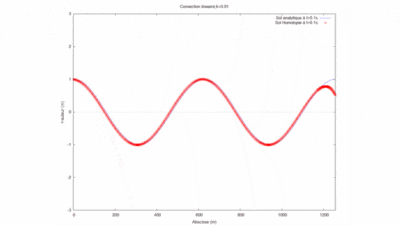
On regarde la convergence de la méthode par homotopie en fonction du produit kL.
Cas kL=0,25 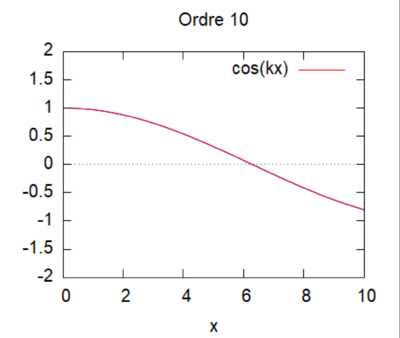
Cas N°2
Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_{x} =ik(2−\phi) $ et réflexion totale amont $ \phi_{x}=0 $.
Méthode analytique
Comme pour le cas N°1, l'équation de Berkhoff à une dimension s'écrit $ \phi_{xx} + k^2\phi = 0 $
Ce qui nous donne comme forme pour $ \phi $ : $ \phi(x) = Ae^{ikx} + Be^{-ikx} $
On peut déterminer les constantes A et B avec les conditions initiales de ce cas.
$ \phi_{x}(0) = ik(2 - \phi(0)) \iff ik(A - B) = ik(2 - A - B) $ $ \iff A = 1 $
Et $ \phi_{x}(L) = 0 \iff ik(Ae^{ikL} - Be^{-ikL}) = 0 \iff B = e^{2ikL} $
Ainsi $ \phi(x)= e^{ikx} + e^{2ikL}e^{-ikx} $
La solution réelle associée à cette fonction est $ h(x) = cos(kx) + cos(2kL+kx) $
Méthode par homotopie
En procédant de la même manière que dans le cas 1 on retrouve comme relation d'homotopie :
$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $
Ordre 0
Tout d'abord, à l'ordre 0:
$ \phi_{0,xx}(x)=0 $
Par intégration on a :
$ \phi_0(x)=Ax+B $
Avec les conditions aux limites : $ \phi_{0,x}^0=ik(2-\phi) $ et $ \phi_{0, x}^L=0 $
On a :
$ A = 0 $ et $ B = 2 $
Donc $ \phi_0(x)=2 $
Ordre 1
Ensuite, pour l'ordre 1:
On a $ \phi_{1,xx}(x) = -k^{2}\phi_0(x) $
donc $ \phi_1 (x) = -k^2x^2 + Ax + B $
Avec les conditions initiales on trouve pour A et B :
$ A = 2k^2L $ et $ B = 2ikL $
Donc $ \phi_1 (x) = - k^2x^2 + 2k^2Lx + 2ikL $
Etude de sensibilité
Cas N°3
Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec une pente de fond constante (s=cst). L'entrée se fait par l'aval avec une onde de fréquence unitaire $ \phi_{x} =ik(2−\phi) $ et la sortie en amont $ \phi_{x}(x=L)=ik\phi(x=L) $.
Résolution analytique
Le problème est complexifié puisque H(x) n'est plus égal à $ H_0 $ mais à $ H_0-sx $.
On a toujours $ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $ mais avec $ C=C_g=\sqrt{gH(x)} $
Soit $ {\displaystyle H(x)\frac{\partial^2 \phi}{\partial x^2} -\frac{\partial \phi}{\partial x} + k^2H(x) \phi = 0} $
Nous utilisons le changement de variable : $ z=H_0-sx $.
Et nous prenons: $ s = \frac{1/200} \ $.
Nous nous intéressons au cas $ k=ko\sqrt{Ho/H(x)} $.
Soit l'équation à résoudre : $ (H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $
On cherche une solution de la forme de l'équation de Bessel, c'est à dire de la forme : $ z^2\phi_{zz}+z\phi_{z}+(\dfrac{k^2}{s^2})z^2\phi=0 $
$ \phi(z)=AJ_0(\dfrac{k}{s}z)+BY_0(\dfrac{k}{s}z) $
Avec les conditions limites :
$ \phi(x=0)=1 $ et $ \phi_x(x=L)=ik \phi(x=L) $
Ce qui donne avec le changement de variable : $ \phi(z=H_0)=1 $ et $ \phi_z(z=H_0-sL)=ik \phi(z=H_0-sL) $
On obtient au final :
$ {\phi(z)=\frac{iY_0^L - Y_1^L}{J_0^0(iY_0^L - Y_1^L) + Y_0^0 (J_1^L-i J_0^L)} J_0 (2 \alpha \sqrt{z}) + \frac{J_1^L - i J_0^L}{J_0^0 (i Y_0^L-Y_1^L) + Y_0^0 (J_1^L - i J_0^L)} Y_0 (2 \alpha \sqrt{z})} $
Résolution par homotopie
Soit la relation d'homotopie suivante : $ (1-p)\phi_{xx}+p(H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $
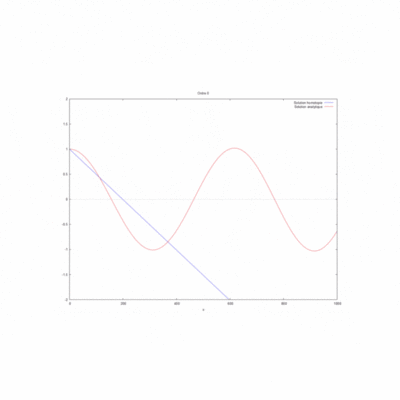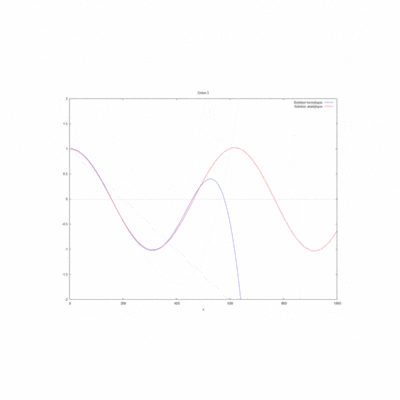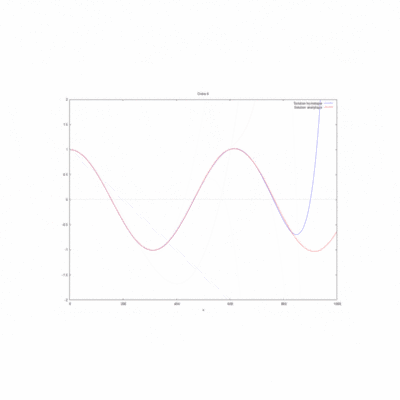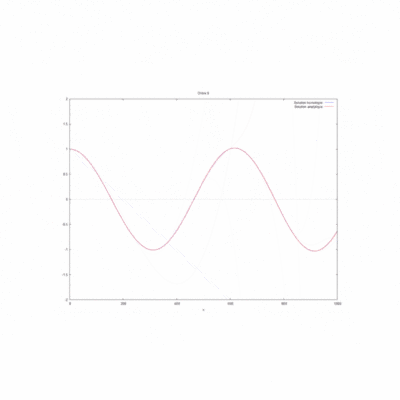
ordre 0
$ \phi_{xx}=0 $ donc on a $ \phi_0=Ax+B $
et avec les conditions initiales on trouve : $ \phi_0=\frac{ik}{1-ikL}x+1 $
La simulation sur WXMaxima nous donne pour le produit kL=1 le gif suivant :
Cas N°4
Dans ce cas nous avons une vague sphérique générée par une source sinusoïdale
$ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $ Et en coordonnées polaires : $ \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $ avec $ r_0=1m $, $ R=100m $ et $ k=0.1m^{-1} $.
 S'abonner à un flux RSS
S'abonner à un flux RSS