Utilisateur:ABET / CASTELLAN / KERGOAT : Différence entre versions
| (42 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | + | = IMPACT DU CHANGEMENT CLIMATIQUE SUR LES CÔTES ET DANS LES ESTUAIRES = | |
| − | + | = Contexte = | |
| Ligne 13 : | Ligne 13 : | ||
:<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[Fichier:Le_Signal_Model.jpg]] </div> <br/> | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[Fichier:Le_Signal_Model.jpg]] </div> <br/> | ||
| − | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> Le bâtiment Le Signal, un symbole de l’érosion côtière en France (Gironde), d’après Le Monde. </div> <br/> |
| − | + | =Méthode homotopique et équation de Berkhoff= | |
L’objectif de l’homotopie est de résoudre des équations différentielles et des intégrales. A partir d’une solution connue relativement simple, elle permet de converger vers une solution plus complète grâce à un paramètre p qui varie entre 0 et 1. Il assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre. | L’objectif de l’homotopie est de résoudre des équations différentielles et des intégrales. A partir d’une solution connue relativement simple, elle permet de converger vers une solution plus complète grâce à un paramètre p qui varie entre 0 et 1. Il assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre. | ||
| − | Elle | + | L'équation de Berkhoff permet de modéliser des ondes de houle. Elle tient compte de la réfraction, de la diffraction et de la réflexion des ondes. |
| − | |||
| − | |||
| + | = Etude des différents cas = | ||
| − | |||
| + | == <span style="color:crimson">Cas n°1</span> == | ||
| − | |||
| + | On se place dans le cas d’un canal monodimensionnel plat de longueur L avec une fréquence d’entrée au niveau de l’aval <math>\phi^{0} = 1</math> et une sortie libre au niveau de l’amont avec <math>\phi_{x}^{L} = ik\phi^{L} </math> | ||
| − | + | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[File:Cas_1_Model.png|600px]]</div> <br/> | |
| − | ==== Résolution Analytique | + | === <span style="color:seagreen">Résolution Analytique</span> === |
| Ligne 66 : | Ligne 65 : | ||
Ce qui nous donne: | Ce qui nous donne: | ||
| − | <math> \boxed{h(x,t) = Re(\phi(x | + | <span style="color:seagreen"><math> \boxed{h(x,t) = Re(\phi(x)\times{e}^{-i \omega t}) = cos(kx)cos(\omega t) - sin(kx) cos(\omega t) =cos(kx-\omega t)} </math></span><br> |
| − | ==== Résolution par homotopie | + | === <span style="color:RoyalBlue">Résolution par homotopie </span>=== |
| Ligne 87 : | Ligne 86 : | ||
L’équation générale d’homotopie avec la décomposition s’écrit donc | L’équation générale d’homotopie avec la décomposition s’écrit donc | ||
| − | <math>\boxed{(1-p)(\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ...) + p ( \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... + k^2 | + | <math>\boxed{(1-p)(\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ...) + p ( \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... + k^2(\phi_0(x) + p\phi_1(x) + p^2\phi_3(x) + p^3\phi_3(x) + ... ) = 0} </math> |
| − | + | ====Ordre 0 ==== | |
| Ligne 104 : | Ligne 103 : | ||
On a donc | On a donc | ||
| − | <math>\phi_0 (x) = \frac{ik}{1-ikL} x + 1</math> | + | <span style="color:RoyalBlue"><math>\boxed{\phi_0 (x) = \frac{ik}{1-ikL} x + 1}</math></span><br> |
| − | + | ====Ordre 1==== | |
| Ligne 115 : | Ligne 114 : | ||
<math>(1-p)(\phi_{0,xx} + p\phi_{1,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + k^2\phi_0) = 0</math> | <math>(1-p)(\phi_{0,xx} + p\phi_{1,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + k^2\phi_0) = 0</math> | ||
| − | On a vu à l’ordre 0 que <math>\phi_{0,xx} = 0 donc \phi_{1,xx} = -k^2\phi_0 \Rightarrow \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B</math> | + | On a vu à l’ordre 0 que <math>\phi_{0,xx} = 0 </math> donc <math> \phi_{1,xx} = -k^2\phi_0 \Rightarrow \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B</math> |
| Ligne 121 : | Ligne 120 : | ||
Conditions aux limites | Conditions aux limites | ||
<math> | <math> | ||
| − | \begin{cases} \phi_1^0 = 0 = B \\\ phi_{1,x}^L = ik \phi_1^L \end{cases} | + | \begin{cases} \phi_1^0 = 0 = B \\ \phi_{1,x}^L = ik \phi_1^L \end{cases} |
</math> | </math> | ||
| − | On obtient après calculs <math>\boxed{\phi_1(x) = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} x - k^2(\frac{ik}{6-ikL} x^3 + \frac{1}{2} x^2)} </math> | + | On obtient après calculs <span style="color:RoyalBlue"><math>\boxed{\phi_1(x) = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} x - k^2(\frac{ik}{6-ikL} x^3 + \frac{1}{2} x^2)} </math></span><br> |
| − | + | ====Ordre 2==== | |
Pour simplifier l'écriture on pose <math>\alpha = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2}</math> et <math>\beta = \frac{ik}{6-ikL}</math> | Pour simplifier l'écriture on pose <math>\alpha = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2}</math> et <math>\beta = \frac{ik}{6-ikL}</math> | ||
| Ligne 141 : | Ligne 140 : | ||
<math> | <math> | ||
| − | \begin{cases} \phi_2^0 = B \\ \phi_{2,x}^L = ik\phi_2 | + | \begin{cases} \phi_2^0 = B \\ \phi_{2,x}^L = ik\phi_2^L = ik[-k^2\int\int(\alpha x - k^2(\beta x^3 + \frac{1}{2} x^2)) dx dx +AL] = ik [-k^2(\alpha\frac{1}{6} L^3 - k^2 ( \beta \frac{1}{20} L^5 + \frac{1}{24} L^4 + AL)] = -k^2[\alpha \frac{1}{2} L^2 - k^2 ( \beta \frac{1}{4} L^4 + \frac{1}{6} L^3)] + A \end{cases} |
</math> | </math> | ||
| + | Après calculs , on obtient<math> A = \frac{ik}{1-ikL}[-k^2(\frac{1}{6}\alpha L^3 - k^2(\frac{1}{20}\beta L^5 + \frac{1}{24} L^4) - \frac{1}{2}\alpha L^2 + k^2(\frac{1}{4}\beta L^4 + \frac{1}{6} L^3)] </math> | ||
| − | <math> \boxed{\phi_2 = -k^2 [ \frac{1}{6}\alpha x^3 - k^2(\frac{1}{20}\beta x^5 + \frac{1}{24} x^4)] + Ax} </math> | + | <span style="color:RoyalBlue"><math> \boxed{\phi_2(x) = -k^2 [ \frac{1}{6}\alpha x^3 - k^2(\frac{1}{20}\beta x^5 + \frac{1}{24} x^4)] + Ax} </math></span><br> |
| + | === <span style="color:RoyalBlue">Représentation graphique </span>=== | ||
| + | À l'aide d'un logiciel de programmation, nous avons modélisé la solution analytique ainsi que la solution par homotopie avec les données: | ||
| − | = | + | -<math>k=\frac{1}{100}</math> (nombre d'onde en m-1) |
| + | -<math>H=40</math> (profondeur en m) | ||
| + | -<math>c=\sqrt{gH}</math> (célérité de l'onde en m/s) | ||
| − | + | -<math>\lambda=\frac{2\pi}{k}</math> (longueur d'onde en m) | |
| + | -<math>L=2\lambda</math> (longueur du domaine en m) | ||
| − | ==== Résolution Analytique | + | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[File:gif_cas_1.gif|600px]] </div> <br/> |
| + | La solution par homotopie converge bien vers la solution analytique dans ce cas. | ||
| + | |||
| + | === <span style="color:RoyalBlue">Étude de sensibilité </span>=== | ||
| + | Nous avons ensuite cherché à optimiser la solution par homotopie en faisant varier le nombre d'onde (k) tout en gardant les autres paramètres fixes. Dans ce cas, nous avons fixé la longueur du domaine <math>L=12</math> (tous les cas ont été effectué à l'ordre 8): | ||
| + | |||
| + | Pour k=0.01: | ||
| + | [[File:k=0.01.jpg|800px]] | ||
| + | |||
| + | Pour k=0.1: | ||
| + | [[File:k=0.1.jpg|800px]] | ||
| + | |||
| + | Pour k=1: | ||
| + | [[File:k=1.jpg|800px]] | ||
| + | |||
| + | On remarque que plus le k est grand moins la solution par homotopie est précise. Cela vient du fait que pour la longueur du domaine choisit (L=12), le produit kL devient supérieur à 1. Or, le produit kL doit être inférieur à 1 pour que la solution par homotopie converge correctement vers la solution analytique. | ||
| + | |||
| + | |||
| + | == <span style="color:crimson">Cas n°2 </span>== | ||
| + | |||
| + | |||
| + | |||
| + | On se place dans le cas d’un domaine monodimensionnel plat de longueur L avec entrée par l’aval d’une onde de fréquence unitaire et une condition de flux aval <math>\phi_x^{0}=ik(2-\phi^{0})</math> et réflexion totale amont <math>\phi_x^{L}=0</math>. | ||
| + | |||
| + | |||
| + | ===<span style="color:seagreen"> Résolution Analytique</span> === | ||
| Ligne 172 : | Ligne 202 : | ||
Finalement | Finalement | ||
| − | <math>\boxed{\phi(x) = \mathrm{e}^{ikL} | + | <span style="color:seagreen"><math>\boxed{\phi(x) = \mathrm{e}^{ikL} + \mathrm{e}^{ik(2L-x)}} </math></span><br> |
| − | ==== Résolution par homotopie | + | ===<span style="color:RoyalBlue"> Résolution par homotopie</span> === |
| − | + | ====Ordre 0==== | |
On a <math> \phi_0(x) = Ax+B </math> | On a <math> \phi_0(x) = Ax+B </math> | ||
Ce qui nous donne <math>\phi_{0,x}^0 = A =ik(2-B) </math> et <math>\phi_{0,x}^L = A = 0 </math> | Ce qui nous donne <math>\phi_{0,x}^0 = A =ik(2-B) </math> et <math>\phi_{0,x}^L = A = 0 </math> | ||
| − | Donc <math> B = 2 \Rightarrow \boxed{ \phi_0 = 2} </math> | + | Donc <math> B = 2 \Rightarrow</math> <span style="color:RoyalBlue"><math>\boxed{ \phi_0(x) = 2} </math></span><br> |
| − | + | ====Ordre 1==== | |
En partant de la relation d'homotopie on obtient comme pour le premier cas : | En partant de la relation d'homotopie on obtient comme pour le premier cas : | ||
| Ligne 191 : | Ligne 221 : | ||
<math>\phi_{1,xx} + k^2\phi_0 = 0 </math> donc <math>\phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B </math> | <math>\phi_{1,xx} + k^2\phi_0 = 0 </math> donc <math>\phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B </math> | ||
| − | Soit <math> | + | Soit <math>\phi_{1} = -k^2x^2 + Ax + B</math> et <math>\phi_{1,x} = -2xk^2 + A </math> |
Conditions aux limites | Conditions aux limites | ||
| Ligne 198 : | Ligne 228 : | ||
</math> | </math> | ||
| − | Donc B = 2(1 + iLk) | + | Donc <math>B = 2(1 + iLk) </math> |
| − | Au final <math>\phi_1 = - k^2x^2 + 2xLk^2 + 2(1 + ikL) </math> | + | Au final <span style="color:RoyalBlue"><math>\boxed{\phi_1(x) = - k^2x^2 + 2xLk^2 + 2(1 + ikL)} </math></span><br> |
| − | + | ====Ordre 2==== | |
Ici <math> \phi_{2,xx} + k^2\phi_0 = 0 \Rightarrow \phi_2 = -k^2\int\int\phi_{0}dxdx +Ax + B = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + Ax + B </math> | Ici <math> \phi_{2,xx} + k^2\phi_0 = 0 \Rightarrow \phi_2 = -k^2\int\int\phi_{0}dxdx +Ax + B = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + Ax + B </math> | ||
| Ligne 212 : | Ligne 242 : | ||
</math> | </math> | ||
| − | Donc B = 2 ( 1 - kL^2 ) | + | Donc <math>B = 2 ( 1 - kL^2 )</math> |
| − | Au final, on a <math>\boxed{\phi_2 = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + -2ik^{2}L^{2}x + B = 2 ( 1 - kL^2 )}</math> | + | Au final, on a <span style="color:RoyalBlue"><math>\boxed{\phi_2(x) = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + -2ik^{2}L^{2}x + B = 2 ( 1 - kL^2 )}</math></span><br> |
| + | === <span style="color:RoyalBlue">Représentation graphique </span>=== | ||
| + | À l'aide d'un logiciel de programmation, nous avons modélisé la solution analytique ainsi que la solution par homotopie: | ||
| − | == | + | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[File:cas2gif.gif|600px]] </div> <br/> |
| + | La solution par homotopie converge bien vers la solution analytique dans ce cas. | ||
| + | == <span style="color:crimson">Cas n°3</span> == | ||
| − | |||
| + | On se place dans le cas d’un canal monodimensionnel de longueur L avec une pente de fond constante (s=constante) avec entrée par l’aval d’une onde de fréquence <math>\phi^{0} = 1</math> et sortie libre en amont <math>\phi_{x}^{L} = ik\phi^{L} </math> | ||
| − | ==== Résolution Analytique | + | |
| + | === <span style="color:seagreen">Résolution Analytique</span> === | ||
On part de l’équation de Berkhoff en considérant qu’on se trouve en petite profondeur soit | On part de l’équation de Berkhoff en considérant qu’on se trouve en petite profondeur soit | ||
<math> \nabla.(CC_{g}\nabla\phi) + k^2\phi = 0</math> avec <math> C = C_{g} =\sqrt{gH} </math> non constantes | <math> \nabla.(CC_{g}\nabla\phi) + k^2\phi = 0</math> avec <math> C = C_{g} =\sqrt{gH} </math> non constantes | ||
| − | + | ====Cas <math> k = k_{0}\sqrt\frac{H_{0}}{H(x)} </math>==== | |
| − | <math> \nabla.(gH\nabla\phi) = gH \frac{\partial^2\phi}{\partial^2x} - g\frac{\partial{H}}{\partial{x}} \frac{\partial\phi}{\partial{x}} </math> | + | La première partie de l'équation peut s'écrire en petite profondeur <math> \nabla.(gH\nabla\phi) = gH \frac{\partial^2\phi}{\partial^2x} - g\frac{\partial{H}}{\partial{x}} \frac{\partial\phi}{\partial{x}} </math> |
On injecte dans l’équation de Berkhoff, on divise l’équation par g et on pose le changement de variable <math> H(x) = z = H_0 - sx \Rightarrow \frac{\partial{H}}{\partial{x}} = -s \frac{\partial{H}}{\partial{z}} </math> pour obtenir <math> H \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k^{2}H\phi = 0 </math> | On injecte dans l’équation de Berkhoff, on divise l’équation par g et on pose le changement de variable <math> H(x) = z = H_0 - sx \Rightarrow \frac{\partial{H}}{\partial{x}} = -s \frac{\partial{H}}{\partial{z}} </math> pour obtenir <math> H \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k^{2}H\phi = 0 </math> | ||
| Ligne 236 : | Ligne 271 : | ||
En prenant en compte la condition sur k, on obtient <math> (H_{0} - sx) \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k_{0}^{2}H_{0}\phi = 0 </math> | En prenant en compte la condition sur k, on obtient <math> (H_{0} - sx) \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k_{0}^{2}H_{0}\phi = 0 </math> | ||
| − | On note que <math> \frac{\partial\phi}{\partial{x}} = - s \frac{\partial\phi}{\partial{z}} et \frac{\partial^2\phi}{\partial^2{x}} = | + | On note que <math> \frac{\partial\phi}{\partial{x}} = - s \frac{\partial\phi}{\partial{z}} et \frac{\partial^2\phi}{\partial^2{x}} = s^{2} \frac{\partial^2\phi}{\partial^2{z}} </math> |
| − | Soit en multipliant par <math>z</math> et en divisant par <math>s^2</math> l’équation devient <math> | + | Soit en multipliant par <math>z</math> et en divisant par <math>s^2</math> l’équation devient <math>z^{2}\frac{\partial^2\phi}{\partial^2{z}} + z\frac{\partial\phi}{\partial{z}} + \frac{k_{0}^{2}}{s^{2}}zH_{0}\phi </math> que l’on peut associer à une équation de Bessel, il faut poser <math> \alpha^{2} = \frac{k_{0}^{2} H_{0}}{s^2} </math> on obtient <math> z^{2}\phi_{zz} + z\phi_z + \alpha^{2}z\phi = 0 </math> |
On pose <math>A</math> et <math>B</math> deux constantes et <math>J_0</math> et <math>Y_0</math> des fonction de Bessel respectivement de première et de deuxième espèce d’ordre 0. On pose alors la solution <math> \phi(z) = A J_{0}(2\alpha\sqrt{z}) + B Y_{0}(2\alpha\sqrt{z}) </math> | On pose <math>A</math> et <math>B</math> deux constantes et <math>J_0</math> et <math>Y_0</math> des fonction de Bessel respectivement de première et de deuxième espèce d’ordre 0. On pose alors la solution <math> \phi(z) = A J_{0}(2\alpha\sqrt{z}) + B Y_{0}(2\alpha\sqrt{z}) </math> | ||
<math> | <math> | ||
| − | \begin{cases} | + | \begin{cases} \phi^{x=0} = \phi(z=H_{0}) = AJ_{0}(2\alpha\sqrt{H_{0}}) + BY_{0}(2\alpha\sqrt{H_{0}}) = 1 \Rightarrow A = \frac{1 - BY_{0}(2\alpha\sqrt{H_{0}})}{J_{0}(2\alpha\sqrt{H_{0}})} \\ \phi_{x}^{x=L} = -s \phi_{z}(z=H_{0}-sL=z_{L}) = ik\phi(z=H_{0}-sL) \Rightarrow \phi_z^{z_{L}} = \frac{ik}{s} (AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}})) = \frac{\alpha}{\sqrt{z_{L}}} (AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}})) \Rightarrow i(AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}})) = AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}}) \\ \Rightarrow B = A\frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})} \end{cases} |
</math> | </math> | ||
| − | On trouve alors <math> A = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})} </math> et <math>B = \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}}(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}}(J_{1}(2\alpha\sqrt{z_{L}} - iJ_{0}(2\alpha\sqrt{z_{L}})} </math> | + | On trouve alors <math> A = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} </math> et <math>B = \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} </math> |
| − | Finalement <math> \boxed{\phi = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})} J_{0}(2\alpha\sqrt{z}) + \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}}(iY_{0}(2\alpha\sqrt{z_{L}} - Y_{1}(2\alpha\sqrt{z_{L}}) + Y_{0}(2\alpha\sqrt{H_{0}}(J_{1}(2\alpha\sqrt{z_{L}} - iJ_{0}(2\alpha\sqrt{z_{L}})} Y_{0}(2\alpha\sqrt{z})} </math> | + | Finalement |
| + | <span style="color:seagreen"><math>\boxed{\phi(x) = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} J_{0}(2\alpha\sqrt{z}) + \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} Y_{0}(2\alpha\sqrt{z})}</math></span><br> | ||
| − | ==== Résolution par homotopie | + | === <span style="color:RoyalBlue">Résolution par homotopie </span>=== |
On prend l'équation générale d'homotopie adapté au changement de variable telle que : <math> (H_{0} - sx) \phi_{xx} - s\phi_{x} + k_{0}^{2}H_{0}\phi = 0 </math> | On prend l'équation générale d'homotopie adapté au changement de variable telle que : <math> (H_{0} - sx) \phi_{xx} - s\phi_{x} + k_{0}^{2}H_{0}\phi = 0 </math> | ||
| − | + | ====Ordre 0==== | |
A l'ordre 0, on a <math>\phi_{0,xx} = 0 </math> soit <math> \phi_{0} = Ax + B </math> | A l'ordre 0, on a <math>\phi_{0,xx} = 0 </math> soit <math> \phi_{0} = Ax + B </math> | ||
| − | D'après les conditions initiales on a : | + | D'après les conditions initiales on a :<math>\begin{cases} \phi^{0} = 1 = B\\ \phi_{x}^{L} = ik\phi^{L} \end{cases}</math> |
| − | <math> | + | On retrouve la même solution que pour l'ordre 0 du cas 1 tel que <span style="color:RoyalBlue"><math> \boxed{\phi_{0}(x) = \frac{ik}{1-ikL} x + 1} </math></span><br> |
| − | \ | + | |
| − | </math> | + | |
| − | + | ====Ordre 1==== | |
| − | + | Tout comme dans les autre cas on a <math>\phi_{0,xx} = 0 </math> donc après calculs sur l’équation d’homotopie, on obtient <math> \boxed{\phi_{1,xx} + (H_{0} - sx)\phi_{0,xx} - s\phi_{0,x} + k_{0}^2H_{0}\phi_{0} = 0}</math> | |
| − | + | Soit <math> \phi_{1,xx} = s\phi_{0,x} - k^2H_{0}\phi_{0} = -s(\frac{ik}{1-ikL}) - k^{2}H_{0}(\frac{ik}{1-ikL}x + 1) </math> | |
| − | + | <math> \phi_{1,x} = -s(\frac{ik}{1-ikL})x - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}x^{2} + x) + A </math> | |
| − | + | ||
| − | + | ||
| − | + | <math> \phi_{1} = -s(\frac{ik}{2(1-ikL)})x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + Ax + B</math> | |
| − | + | Conditions initiales <math>\begin{cases} \phi_{1}^{0} = 1 = B \\ \phi_{1,x}^{L} = -s(\frac{ik}{1-ikL}))L - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}L^{2} + L) + A = ik (-s(\frac{ik}{2(1-ikL)}L^{2} - k^{2}H_{0}(\frac{ik}{6(1-ikL)}L^{3} + \frac{L^{2}}{2}) + AL + 1) \end{cases}</math> | |
| − | + | ||
En posant <math> \alpha = \frac{ik}{1 - ikL} </math> on obtient | En posant <math> \alpha = \frac{ik}{1 - ikL} </math> on obtient | ||
| − | + | <math> -s\alpha L - k_{0}^{2}H_{0}(\frac{\alpha}{2}L^{2} + L) + A = ik (-s\frac{\alpha}{2}L^{2} - k_{0}^{2}H_{0}(\frac{\alpha}{6}L^{3} + \frac{L^{2}}{2}) + AL + 1))</math> | |
| − | === Cas n°4 | + | Soit <math> A(1 - ikL) = s\alpha(L - ik\frac{L^{2}}{2}) - k_{0}^{2}H_{0}(-\frac{\alpha}{2}L^{2} - L + ik\frac{\alpha}{6}L^{3} +ik\frac{L^{2}}{2}) + ik </math> |
| + | |||
| + | En divisant et en remplaçant <math> \alpha </math> par son expression, on trouve : | ||
| + | <math> A = \frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}) - \frac{(ik)^{2}k_{0}^{2}H_{0}L^{2}}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) + \frac{ik}{1 - ikL} </math> | ||
| + | |||
| + | Au final | ||
| + | <span style="color:RoyalBlue"><math> \boxed{\phi_{1}(x) = -s(\frac{ik}{2(1-ikL)}x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + (\frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}) - \frac{(ik)^{2}k_{0}^{2}H_{0}L^{2}}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) + \frac{ik}{1 - ikL}) x + 1}</math> </span><br> | ||
| + | |||
| + | == <span style="color:crimson">Cas n°4</span> == | ||
On s'intéresse ici à une vague générée par une source périodique sinusoïdale. On se place en grande profondeur, une source ponctuelle est placée autour d'un cercle de rayon <math> r_0</math>, le cercle est lui-même centré sur un domaine circulaire de rayon R. | On s'intéresse ici à une vague générée par une source périodique sinusoïdale. On se place en grande profondeur, une source ponctuelle est placée autour d'un cercle de rayon <math> r_0</math>, le cercle est lui-même centré sur un domaine circulaire de rayon R. | ||
| Ligne 299 : | Ligne 338 : | ||
On prendra les valeurs numériques suivantes <math> R_{0} = 1m, R = 100m </math> et <math>k = 0.1m^{-1}</math> | On prendra les valeurs numériques suivantes <math> R_{0} = 1m, R = 100m </math> et <math>k = 0.1m^{-1}</math> | ||
| − | ==== | + | ===<span style="color:seagreen"> Résolution Analytique</span> === |
On retrouve une équation du type Bessel traitée dans le cas 3, la solution est du type <math>\phi(r) = AJ_{0}^{kr} + BY_{0}^{kr} \Rightarrow \phi_{r}^{r} = k(AJ_{1}^{kr} + BY_{1}^{kr}) </math> | On retrouve une équation du type Bessel traitée dans le cas 3, la solution est du type <math>\phi(r) = AJ_{0}^{kr} + BY_{0}^{kr} \Rightarrow \phi_{r}^{r} = k(AJ_{1}^{kr} + BY_{1}^{kr}) </math> | ||
| Ligne 311 : | Ligne 350 : | ||
<math> B = \frac{1-AJ_{0}^{kr_{0}}}{Y_{0}^{kr_{0}}}</math> et <math>A = -B\frac{ikY_{0}^{kR} + kY_{1}^{kR}}{ikJ_{0}^{kR} + kJ_{1}^{kR}} </math> | <math> B = \frac{1-AJ_{0}^{kr_{0}}}{Y_{0}^{kr_{0}}}</math> et <math>A = -B\frac{ikY_{0}^{kR} + kY_{1}^{kR}}{ikJ_{0}^{kR} + kJ_{1}^{kR}} </math> | ||
| − | Après calcul on obtient <math> B = \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR}) | + | Après calcul on obtient |
| + | <math> B = \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})} </math> et <math> A = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})} </math> | ||
| − | Soit <math>\boxed{\phi(r) = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} ( ikY_{0}^{kR} + kY_{1}^{kR}) | + | Soit |
| + | <span style="color:seagreen"><math> \boxed{\phi(r) = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})}J_{0}^{kr} + \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})}Y_{0}^{kr}} </math></span><br> | ||
| − | ==== | + | ===<span style="color:RoyalBlue"> Résolution par homotopie </span>=== |
On part de l’équation d’homotopie suivante <math> (1-p)\phi_{rr} + p\phi_{rr} + \frac{1}{r}\phi_{r} + k^2\phi = 0 </math> | On part de l’équation d’homotopie suivante <math> (1-p)\phi_{rr} + p\phi_{rr} + \frac{1}{r}\phi_{r} + k^2\phi = 0 </math> | ||
| − | + | ====Ordre 0==== | |
On reprend les mêmes conditions que précédemment telles que <math> \phi_{0,rr} = 0 </math> ce qui implique <math> \phi_{0} = Ar + B </math> | On reprend les mêmes conditions que précédemment telles que <math> \phi_{0,rr} = 0 </math> ce qui implique <math> \phi_{0} = Ar + B </math> | ||
| Ligne 330 : | Ligne 371 : | ||
Après résolution, on obtient <math> B = \frac{1 - ikR}{1 + ik(r_{0} - R)} </math> et <math> A = \frac{ik}{1 + ik(r_{0} - R)} </math> | Après résolution, on obtient <math> B = \frac{1 - ikR}{1 + ik(r_{0} - R)} </math> et <math> A = \frac{ik}{1 + ik(r_{0} - R)} </math> | ||
| − | Au final pour l’ordre 0 <math>\boxed{\phi_{0} = \frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}} </math> | + | Au final pour l’ordre 0 <span style="color:RoyalBlue"><math>\boxed{\phi_{0}(r) = \frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}} </math></span><br> |
| − | + | ====Ordre 1==== | |
On reprend l’équation générale d’homotopie pour un ordre 1, on trouve <math>\phi_{1,rr} + \frac{1}{r} \phi_{0,r} + k^2\phi_{0} = 0 </math> | On reprend l’équation générale d’homotopie pour un ordre 1, on trouve <math>\phi_{1,rr} + \frac{1}{r} \phi_{0,r} + k^2\phi_{0} = 0 </math> | ||
| Ligne 344 : | Ligne 385 : | ||
Conditions aux limites : | Conditions aux limites : | ||
<math> | <math> | ||
| − | \begin{cases} \phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r_{0}^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} R^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} R + C_{1} = | + | \begin{cases} \phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r_{0}^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} R^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} R + C_{1} = -ik (R ln(R) - R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} R^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} R^2 + C_{1}R + C_{2} \end{cases} |
</math> | </math> | ||
En reprenant les notations à l'ordre à pour <math>A</math> et <math>B</math>, on a | En reprenant les notations à l'ordre à pour <math>A</math> et <math>B</math>, on a | ||
| − | + | <math> | |
| + | \begin{cases}\phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) A - \frac{k^2}{6} A r_{0}^3 - \frac{k^2}{2} B r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) A - \frac{k^2}{2} A R^2 - k^2 B R + C_{1} = -ik (R ln(R) - R) A - \frac{k^2}{6} A R^3 - \frac{k^2}{2}B R^2 + C_{1}R + C_{2} \end{cases}</math> | ||
| + | |||
| + | Après calcul, on trouve les constantes suivantes <math> | ||
| + | \begin{cases} C_1=(6Ar_{0}ln(r_{0})+3Bk^{2}r_{0}^{2}-6Ar_{0}+(-AR^{3}-3BR^{2}+(6B+3A)R+Ar_{0}^{3})k^{2}+AR\frac{(6i-6iln(R))k+6Aln(R)+6)}{6} | ||
| + | \\C_2=-(6AR-6A)r_{0}ln(r_{0})+(3BR-3B)k^{2}r^{2}+(6A-6AR)r_{0}+(-AR^{4}-3BR^{3}+(6B+3A)R^{2}+Ar^{3}R-Ar^{3})k^{2}+AR^{2}\frac{(6i-6iln(R))k+R(6Aln(R)+6)-6)}{6} | ||
| + | \end{cases} </math> | ||
| + | |||
| + | Finalement on a bien <span style="color:RoyalBlue"><math>\boxed{\phi_{1}(x) = - (r ln(r) - r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r^2 + C_{1}r + C_{2}}</math></span><br> | ||
| + | |||
| + | = Proposition d’application = | ||
| + | |||
| + | L’homotopie appliquée a l’équation de Berkhoff permet de modéliser et de prévoir l’impact de la houle sur les littoraux, de manière plus ou moins précise. Cette méthode s’applique à la houle, mais elle peut aussi être utile dans la modélisation d’autres phénomènes complexes qui mettent en jeu la propagation d’ondes. | ||
| + | On voit nettement l’utilité de cette méthode et son application concrète sur les littoraux. En anticipant l’impact de la houle sur la côte, on est capable de bâtir des infrastructures spécifiques adaptées à chaque littoral, pour réduire l’érosion et ralentir les effets du réchauffement climatique sur ces espaces protégés et caractériels que sont les littoraux. | ||
| + | |||
| + | Pour illustration, on peut d’après les études de propagation de la houle choisir le type de digue adapté pour réduire l’énergie des vagues lorsqu'elles se fracassent sur le littoral: | ||
| + | |||
| + | :<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> [[Fichier:Conlusion_Model.png|800px]]</div> <br/> | ||
| + | |||
| + | Voici une vidéo qui résume et vulgarise le projet : | ||
| − | + | https://www.canva.com/design/DAFlQC5jjJc/ZkFLICUqtgfkvDyHIPBdvg/watch?utm_content=DAFlQC5jjJc&utm_campaign=designshare&utm_medium=link&utm_source=publishsharelink | |
Version actuelle en date du 15 juin 2023 à 10:08
Sommaire |
[modifier] IMPACT DU CHANGEMENT CLIMATIQUE SUR LES CÔTES ET DANS LES ESTUAIRES
[modifier] Contexte
”Environ 1 milliard de personnes pourraient vivre d’ici 2050 dans des zones côtières menacées par la montée des eaux et les épisodes de submersions marines lors des tempêtes” , alertent les experts de l’ONU.
C’est dans ce climat d’incertitude et d’insécurité qu’évoluent les populations côtières, c’est à dire plus de 60 pourcents de la population mondiale. L’érosion des côtes et l’impact de la houle sur les littoraux s’accélèrent avec le changement climatique. Ce phénomène doit donc être étudié afin d’anticiper l’érosion des littoraux et de réaliser des aménagements adaptés. C’est pourquoi des outils mathématiques sont nécessaires pour prévoir l’impact des houles sur le littoral.
C’est en appliquant le principe de l’homotopie à l'équation de Berkhoff que nous pouvons modéliser l’impact du réchauffement climatique et de la houle sur les côtes.
- Le bâtiment Le Signal, un symbole de l’érosion côtière en France (Gironde), d’après Le Monde.
[modifier] Méthode homotopique et équation de Berkhoff
L’objectif de l’homotopie est de résoudre des équations différentielles et des intégrales. A partir d’une solution connue relativement simple, elle permet de converger vers une solution plus complète grâce à un paramètre p qui varie entre 0 et 1. Il assure une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre.
L'équation de Berkhoff permet de modéliser des ondes de houle. Elle tient compte de la réfraction, de la diffraction et de la réflexion des ondes.
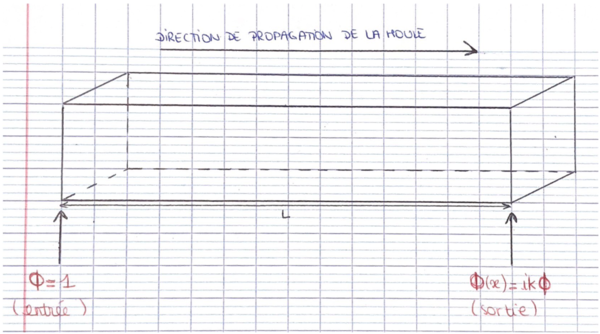
[modifier] Etude des différents cas
[modifier] Cas n°1
On se place dans le cas d’un canal monodimensionnel plat de longueur L avec une fréquence d’entrée au niveau de l’aval $ \phi^{0} = 1 $ et une sortie libre au niveau de l’amont avec $ \phi_{x}^{L} = ik\phi^{L} $
[modifier] Résolution Analytique
On souhaite résoudre l’équation du modèle de Berkhoff $ \boxed{\nabla.(CC_{g}\nabla\phi) + k^2\phi = 0} $
On pose une solution du potentiel $ \phi = A\mathrm{e}^{ikx} + B\mathrm{e}^{-ikx} $ et on résoud l’équation à l’aide des conditions aux limites
- Condition 1 :
$ \phi(x=0)=1 $
$ \phi(x=0) = A + B = 1 \Rightarrow A = 1 - B $
- Condition 2 :
$ \phi_x(L) = ik\phi(L) $
$ \phi_x(L) = ikA\mathrm{e}^{ikL} - ikB\mathrm{e}^{-ikL} = ik(A\mathrm{e}^{ikL} + B\mathrm{e}^{-ikL}) $
Il vient: $ 2ikB\mathrm{e}^{-ikL} \Rightarrow B = 0 \Rightarrow A = 1 $
Finalement
$ \phi(x)={e}^{ikx} = cos(kx) + isin(kx) $
Ce qui nous donne:
$ \boxed{h(x,t) = Re(\phi(x)\times{e}^{-i \omega t}) = cos(kx)cos(\omega t) - sin(kx) cos(\omega t) =cos(kx-\omega t)} $
[modifier] Résolution par homotopie
On reprend les mêmes conditions initiales mais cette fois ci on part de la relation d’homotopie $ \boxed{(1-p) \phi_{xx} + p(\phi_{xx}+k^2\phi) = 0} $
On introduit la décomposition de φ telle que:
$ \phi(x,p) = \phi_0(x) + p\phi_1(x) + p^2\phi_3(x) + p^3\phi_3(x) + ... $
$ \phi_{xx}(x) = \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... $
L’équation générale d’homotopie avec la décomposition s’écrit donc
$ \boxed{(1-p)(\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ...) + p ( \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^2\phi_{2,xx}(x) + p^3\phi_{3,xx}(x) + ... + k^2(\phi_0(x) + p\phi_1(x) + p^2\phi_3(x) + p^3\phi_3(x) + ... ) = 0} $
[modifier] Ordre 0
On reprend l’équation à l’ordre 0 telle que: $ (1-p)\phi_{0,xx} + p\phi_{0,xx} = 0 \Rightarrow \phi_{0,xx} = 0 \Rightarrow \phi_0 = Ax + B $
Conditions aux limites
$ \begin{cases} \phi_0^0 = 1 = B \\\phi_{0,x}^L = ik\phi_{0}^L = ik(AL + 1) = A \Rightarrow A = \frac{ik}{1-ikL} \end{cases} $
On a donc
$ \boxed{\phi_0 (x) = \frac{ik}{1-ikL} x + 1} $
[modifier] Ordre 1
On reprend l’équation à l’ordre 1 telle que:
$ (1-p)(\phi_{0,xx} + p\phi_{1,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + k^2\phi_0) = 0 $
On a vu à l’ordre 0 que $ \phi_{0,xx} = 0 $ donc $ \phi_{1,xx} = -k^2\phi_0 \Rightarrow \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B $
Conditions aux limites $ \begin{cases} \phi_1^0 = 0 = B \\ \phi_{1,x}^L = ik \phi_1^L \end{cases} $
On obtient après calculs $ \boxed{\phi_1(x) = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} x - k^2(\frac{ik}{6-ikL} x^3 + \frac{1}{2} x^2)} $
[modifier] Ordre 2
Pour simplifier l'écriture on pose $ \alpha = \frac {-k^2L(k^2L^2 + 3ikL - 3)}{(1-ikL)^2} $ et $ \beta = \frac{ik}{6-ikL} $
On reprend l'équation générale à l'ordre 2 telle que $ (1 - p)(\phi_{0,xx} + p\phi_{1,xx} + p^2\phi_{2,xx}) + p(\phi_{0,xx} + p\phi_{1,xx} + p^2\phi_{2,xx} + k^2\phi_0 + k^2p\phi_1 = 0 $
Sachant que $ \phi_{1,xx} = - k^2\phi_0 $ et $ \phi_{0,xx} = 0 $, on obtient :
$ p(-k^2\phi_0 + p^2\phi_{2,xx}) + pk^2\phi_0 + p^2k^2\phi_1 = 0 \Rightarrow \phi_{2,xx} = - k^2\phi_1 \Rightarrow \phi_2 = -k^2 \int\int\phi_1dxdx + Ax + B $
Conditions aux limites
$ \begin{cases} \phi_2^0 = B \\ \phi_{2,x}^L = ik\phi_2^L = ik[-k^2\int\int(\alpha x - k^2(\beta x^3 + \frac{1}{2} x^2)) dx dx +AL] = ik [-k^2(\alpha\frac{1}{6} L^3 - k^2 ( \beta \frac{1}{20} L^5 + \frac{1}{24} L^4 + AL)] = -k^2[\alpha \frac{1}{2} L^2 - k^2 ( \beta \frac{1}{4} L^4 + \frac{1}{6} L^3)] + A \end{cases} $
Après calculs , on obtient$ A = \frac{ik}{1-ikL}[-k^2(\frac{1}{6}\alpha L^3 - k^2(\frac{1}{20}\beta L^5 + \frac{1}{24} L^4) - \frac{1}{2}\alpha L^2 + k^2(\frac{1}{4}\beta L^4 + \frac{1}{6} L^3)] $
$ \boxed{\phi_2(x) = -k^2 [ \frac{1}{6}\alpha x^3 - k^2(\frac{1}{20}\beta x^5 + \frac{1}{24} x^4)] + Ax} $
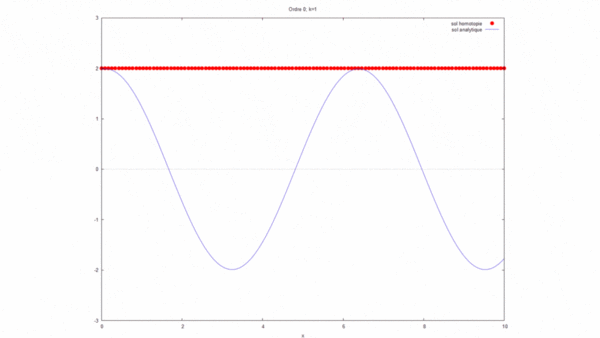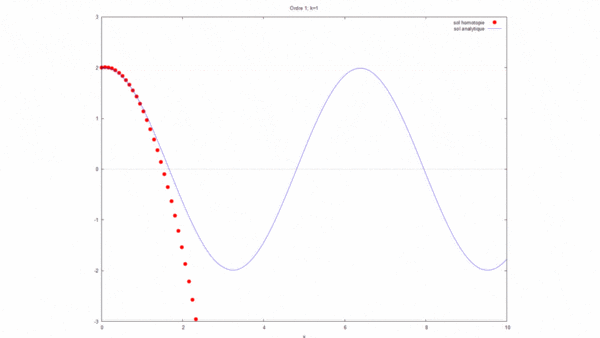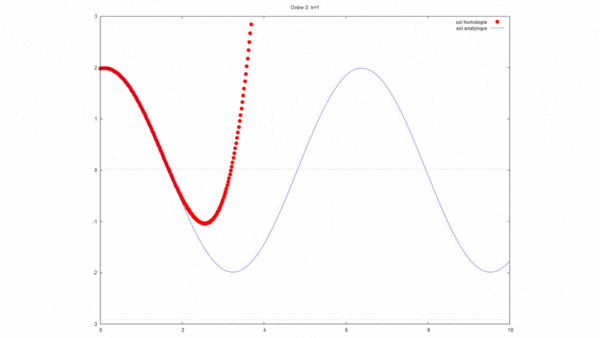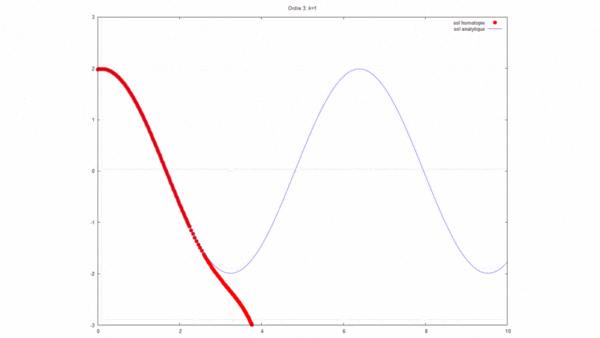
[modifier] Représentation graphique
À l'aide d'un logiciel de programmation, nous avons modélisé la solution analytique ainsi que la solution par homotopie avec les données:
-$ k=\frac{1}{100} $ (nombre d'onde en m-1)
-$ H=40 $ (profondeur en m)
-$ c=\sqrt{gH} $ (célérité de l'onde en m/s)
-$ \lambda=\frac{2\pi}{k} $ (longueur d'onde en m)
-$ L=2\lambda $ (longueur du domaine en m)
La solution par homotopie converge bien vers la solution analytique dans ce cas.
[modifier] Étude de sensibilité
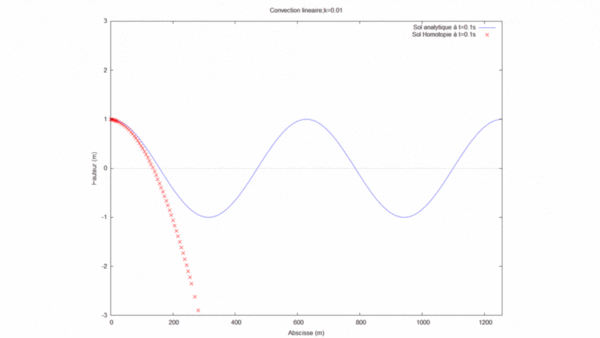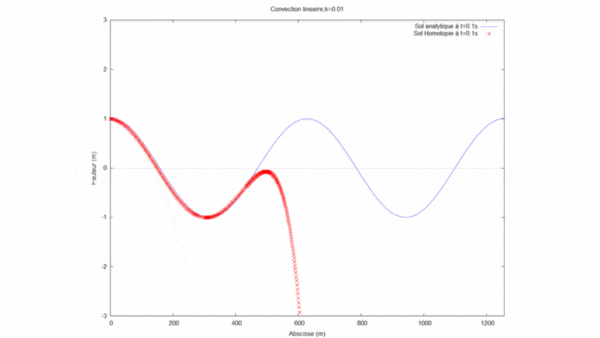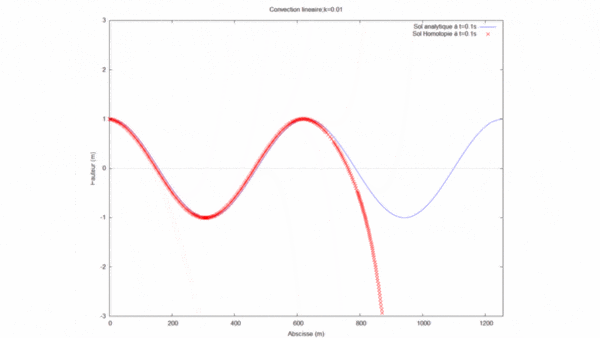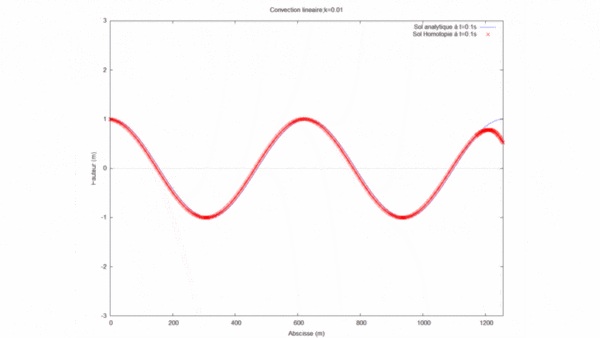
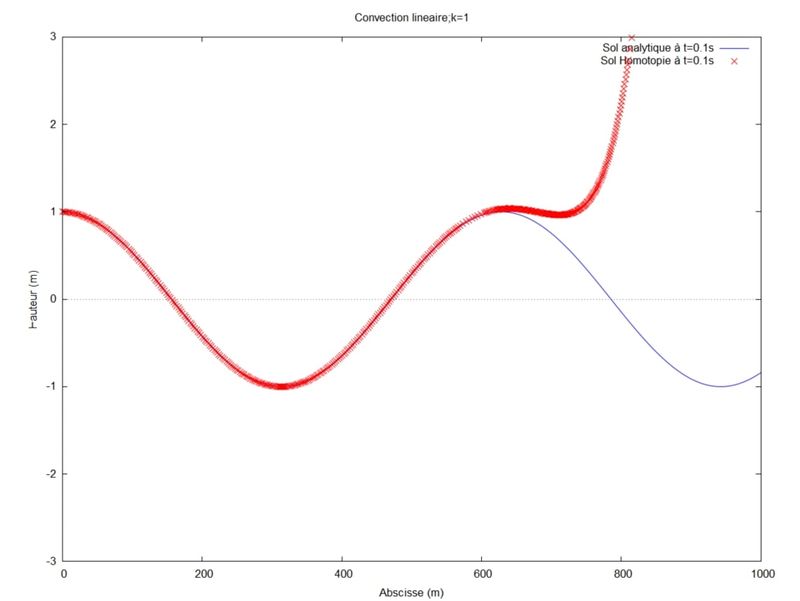
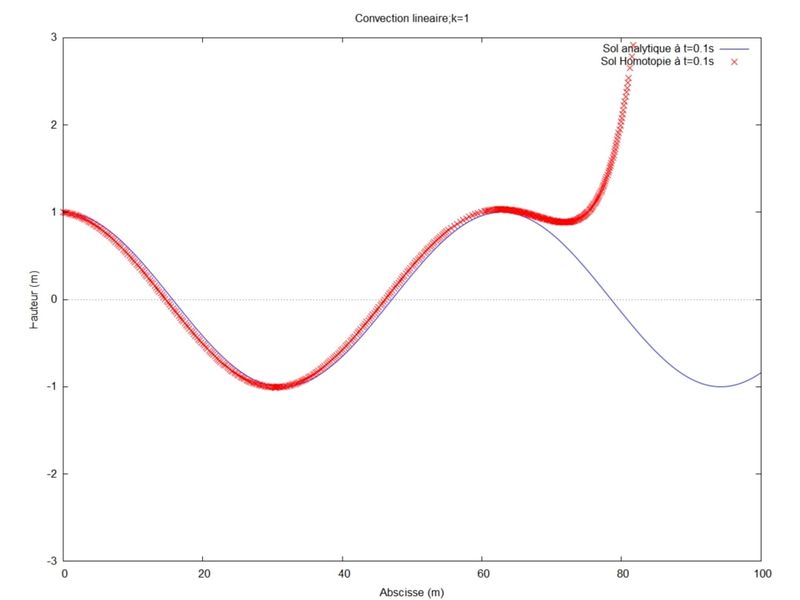
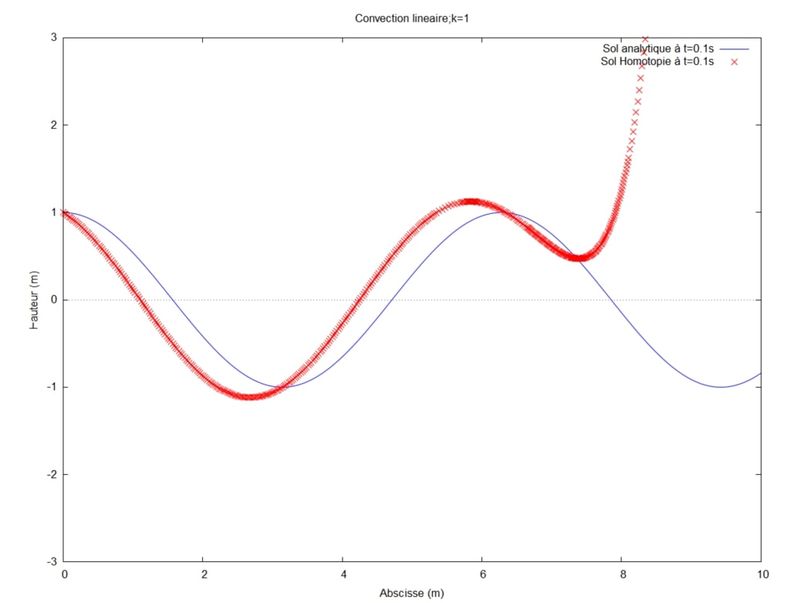
Nous avons ensuite cherché à optimiser la solution par homotopie en faisant varier le nombre d'onde (k) tout en gardant les autres paramètres fixes. Dans ce cas, nous avons fixé la longueur du domaine $ L=12 $ (tous les cas ont été effectué à l'ordre 8):
On remarque que plus le k est grand moins la solution par homotopie est précise. Cela vient du fait que pour la longueur du domaine choisit (L=12), le produit kL devient supérieur à 1. Or, le produit kL doit être inférieur à 1 pour que la solution par homotopie converge correctement vers la solution analytique.
[modifier] Cas n°2
On se place dans le cas d’un domaine monodimensionnel plat de longueur L avec entrée par l’aval d’une onde de fréquence unitaire et une condition de flux aval $ \phi_x^{0}=ik(2-\phi^{0}) $ et réflexion totale amont $ \phi_x^{L}=0 $.
[modifier] Résolution Analytique
Comme dans le cas n°1: On obtient $ \phi = A\mathrm{e}^{ikx} + B\mathrm{e}^{-ikx} $et on résout l’équation à l’aide des conditions aux limites:
- En aval:
$ \phi(x=0) = ik(2-\phi) $ ce qui nous donne $ \phi_x (0) = ikA-ikB=ik(2-A-B) \Rightarrow A=1 $
- En amont:
$ \phi_{x}(x=L) = 0 $ ce qui nous donne $ \phi_x (L) = ikA\mathrm{e}^{ikL} - ikB\mathrm{e}^{-ikL} = 0 \Rightarrow B = \mathrm{e}^{2ikL} $
Finalement
$ \boxed{\phi(x) = \mathrm{e}^{ikL} + \mathrm{e}^{ik(2L-x)}} $
[modifier] Résolution par homotopie
[modifier] Ordre 0
On a $ \phi_0(x) = Ax+B $ Ce qui nous donne $ \phi_{0,x}^0 = A =ik(2-B) $ et $ \phi_{0,x}^L = A = 0 $
Donc $ B = 2 \Rightarrow $ $ \boxed{ \phi_0(x) = 2} $
[modifier] Ordre 1
En partant de la relation d'homotopie on obtient comme pour le premier cas :
$ \phi_{1,xx} + k^2\phi_0 = 0 $ donc $ \phi_1 = -k^2\int\int\phi_{0}dxdx +Ax + B $
Soit $ \phi_{1} = -k^2x^2 + Ax + B $ et $ \phi_{1,x} = -2xk^2 + A $
Conditions aux limites $ \begin{cases} \phi_{1,x}^0 = ik(2 - \phi_1^0) = ik(2 - B) = A \Rightarrow B = 2 - \frac{A}{ik}\\ \phi_{1,x}^L = 0 = -2Lk^2 + A \Rightarrow A = 2Lk^2 \end{cases} $
Donc $ B = 2(1 + iLk) $
Au final $ \boxed{\phi_1(x) = - k^2x^2 + 2xLk^2 + 2(1 + ikL)} $
[modifier] Ordre 2
Ici $ \phi_{2,xx} + k^2\phi_0 = 0 \Rightarrow \phi_2 = -k^2\int\int\phi_{0}dxdx +Ax + B = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + Ax + B $ $ \phi_{2,x} = -k^2\int\phi{1}dx + A = -k^2 ( -k^2\frac{x^3}{3} + Lk^2\frac{x^2}{3} + 2ikLx ) + A $
Conditions aux limites $ \begin{cases} \phi{2,x}^0 = A = ik(2 - \phi^0) = ik ( 2 - B ) \Rightarrow B = 2 - \frac{A}{ik}\\ \phi{2,x}^L = 0 \Rightarrow A = -k^2 ( -k^2\frac{L^3}{3} + k^2\frac{L^3}{3} + 2ikL^2 ) \Rightarrow A = -2ik^{2}L^2 \end{cases} $
Donc $ B = 2 ( 1 - kL^2 ) $
Au final, on a $ \boxed{\phi_2(x) = -k^2 ( -k^2\frac{x^4}{12} + Lk^2\frac{x^3}{3} + ikLx^2 ) + -2ik^{2}L^{2}x + B = 2 ( 1 - kL^2 )} $
[modifier] Représentation graphique
À l'aide d'un logiciel de programmation, nous avons modélisé la solution analytique ainsi que la solution par homotopie:
La solution par homotopie converge bien vers la solution analytique dans ce cas.
[modifier] Cas n°3
On se place dans le cas d’un canal monodimensionnel de longueur L avec une pente de fond constante (s=constante) avec entrée par l’aval d’une onde de fréquence $ \phi^{0} = 1 $ et sortie libre en amont $ \phi_{x}^{L} = ik\phi^{L} $
[modifier] Résolution Analytique
On part de l’équation de Berkhoff en considérant qu’on se trouve en petite profondeur soit $ \nabla.(CC_{g}\nabla\phi) + k^2\phi = 0 $ avec $ C = C_{g} =\sqrt{gH} $ non constantes
[modifier] Cas $ k = k_{0}\sqrt\frac{H_{0}}{H(x)} $
La première partie de l'équation peut s'écrire en petite profondeur $ \nabla.(gH\nabla\phi) = gH \frac{\partial^2\phi}{\partial^2x} - g\frac{\partial{H}}{\partial{x}} \frac{\partial\phi}{\partial{x}} $
On injecte dans l’équation de Berkhoff, on divise l’équation par g et on pose le changement de variable $ H(x) = z = H_0 - sx \Rightarrow \frac{\partial{H}}{\partial{x}} = -s \frac{\partial{H}}{\partial{z}} $ pour obtenir $ H \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k^{2}H\phi = 0 $
En prenant en compte la condition sur k, on obtient $ (H_{0} - sx) \frac{\partial^2\phi}{\partial^2{x}} - s\frac{\partial\phi}{\partial{x}} + k_{0}^{2}H_{0}\phi = 0 $
On note que $ \frac{\partial\phi}{\partial{x}} = - s \frac{\partial\phi}{\partial{z}} et \frac{\partial^2\phi}{\partial^2{x}} = s^{2} \frac{\partial^2\phi}{\partial^2{z}} $
Soit en multipliant par $ z $ et en divisant par $ s^2 $ l’équation devient $ z^{2}\frac{\partial^2\phi}{\partial^2{z}} + z\frac{\partial\phi}{\partial{z}} + \frac{k_{0}^{2}}{s^{2}}zH_{0}\phi $ que l’on peut associer à une équation de Bessel, il faut poser $ \alpha^{2} = \frac{k_{0}^{2} H_{0}}{s^2} $ on obtient $ z^{2}\phi_{zz} + z\phi_z + \alpha^{2}z\phi = 0 $
On pose $ A $ et $ B $ deux constantes et $ J_0 $ et $ Y_0 $ des fonction de Bessel respectivement de première et de deuxième espèce d’ordre 0. On pose alors la solution $ \phi(z) = A J_{0}(2\alpha\sqrt{z}) + B Y_{0}(2\alpha\sqrt{z}) $
$ \begin{cases} \phi^{x=0} = \phi(z=H_{0}) = AJ_{0}(2\alpha\sqrt{H_{0}}) + BY_{0}(2\alpha\sqrt{H_{0}}) = 1 \Rightarrow A = \frac{1 - BY_{0}(2\alpha\sqrt{H_{0}})}{J_{0}(2\alpha\sqrt{H_{0}})} \\ \phi_{x}^{x=L} = -s \phi_{z}(z=H_{0}-sL=z_{L}) = ik\phi(z=H_{0}-sL) \Rightarrow \phi_z^{z_{L}} = \frac{ik}{s} (AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}})) = \frac{\alpha}{\sqrt{z_{L}}} (AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}})) \Rightarrow i(AJ_{0}(2\alpha\sqrt{z_{L}}) + BY_{0}(2\alpha\sqrt{z_{L}})) = AJ_{1}(2\alpha\sqrt{z_{L}}) + BY_{1}(2\alpha\sqrt{z_{L}}) \\ \Rightarrow B = A\frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})} \end{cases} $
On trouve alors $ A = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} $ et $ B = \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} $
Finalement
$ \boxed{\phi(x) = \frac{iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} J_{0}(2\alpha\sqrt{z}) + \frac{J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}})}{J_{0}(2\alpha\sqrt{H_{0}})(iY_{0}(2\alpha\sqrt{z_{L}}) - Y_{1}(2\alpha\sqrt{z_{L}})) + Y_{0}(2\alpha\sqrt{H_{0}})(J_{1}(2\alpha\sqrt{z_{L}}) - iJ_{0}(2\alpha\sqrt{z_{L}}))} Y_{0}(2\alpha\sqrt{z})} $
[modifier] Résolution par homotopie
On prend l'équation générale d'homotopie adapté au changement de variable telle que : $ (H_{0} - sx) \phi_{xx} - s\phi_{x} + k_{0}^{2}H_{0}\phi = 0 $
[modifier] Ordre 0
A l'ordre 0, on a $ \phi_{0,xx} = 0 $ soit $ \phi_{0} = Ax + B $
D'après les conditions initiales on a :$ \begin{cases} \phi^{0} = 1 = B\\ \phi_{x}^{L} = ik\phi^{L} \end{cases} $
On retrouve la même solution que pour l'ordre 0 du cas 1 tel que $ \boxed{\phi_{0}(x) = \frac{ik}{1-ikL} x + 1} $
[modifier] Ordre 1
Tout comme dans les autre cas on a $ \phi_{0,xx} = 0 $ donc après calculs sur l’équation d’homotopie, on obtient $ \boxed{\phi_{1,xx} + (H_{0} - sx)\phi_{0,xx} - s\phi_{0,x} + k_{0}^2H_{0}\phi_{0} = 0} $
Soit $ \phi_{1,xx} = s\phi_{0,x} - k^2H_{0}\phi_{0} = -s(\frac{ik}{1-ikL}) - k^{2}H_{0}(\frac{ik}{1-ikL}x + 1) $
$ \phi_{1,x} = -s(\frac{ik}{1-ikL})x - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}x^{2} + x) + A $
$ \phi_{1} = -s(\frac{ik}{2(1-ikL)})x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + Ax + B $
Conditions initiales $ \begin{cases} \phi_{1}^{0} = 1 = B \\ \phi_{1,x}^{L} = -s(\frac{ik}{1-ikL}))L - k_{0}^{2}H_{0}(\frac{ik}{2(1-ikL)}L^{2} + L) + A = ik (-s(\frac{ik}{2(1-ikL)}L^{2} - k^{2}H_{0}(\frac{ik}{6(1-ikL)}L^{3} + \frac{L^{2}}{2}) + AL + 1) \end{cases} $
En posant $ \alpha = \frac{ik}{1 - ikL} $ on obtient
$ -s\alpha L - k_{0}^{2}H_{0}(\frac{\alpha}{2}L^{2} + L) + A = ik (-s\frac{\alpha}{2}L^{2} - k_{0}^{2}H_{0}(\frac{\alpha}{6}L^{3} + \frac{L^{2}}{2}) + AL + 1)) $
Soit $ A(1 - ikL) = s\alpha(L - ik\frac{L^{2}}{2}) - k_{0}^{2}H_{0}(-\frac{\alpha}{2}L^{2} - L + ik\frac{\alpha}{6}L^{3} +ik\frac{L^{2}}{2}) + ik $
En divisant et en remplaçant $ \alpha $ par son expression, on trouve : $ A = \frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}) - \frac{(ik)^{2}k_{0}^{2}H_{0}L^{2}}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) + \frac{ik}{1 - ikL} $
Au final
$ \boxed{\phi_{1}(x) = -s(\frac{ik}{2(1-ikL)}x^{2} - k_{0}^{2}H_{0}(\frac{ik}{6(1-ikL)}x^{3} + \frac{x^{2}}{2}) + (\frac{sikL}{(1 - ikL)^2}(1 - ik\frac{L}{2}) - \frac{k_{0}^{2}H_{0}L}{1 - ikL}(1 + \frac{ikL}{2(1 + ikL)}) - \frac{(ik)^{2}k_{0}^{2}H_{0}L^{2}}{1 - ikL}(\frac{1}{2} + \frac{L}{6(1 - ikL)}) + \frac{ik}{1 - ikL}) x + 1} $
[modifier] Cas n°4
On s'intéresse ici à une vague générée par une source périodique sinusoïdale. On se place en grande profondeur, une source ponctuelle est placée autour d'un cercle de rayon $ r_0 $, le cercle est lui-même centré sur un domaine circulaire de rayon R. L'équation de Berkhoff s'exprime alors $ \Delta\phi = k^2\phi = 0 $
Avec les conditions initiales suivantes $ \begin{cases} \phi^{r=r_{0}} = 1\\ \phi_{r}^{r=R} = ik\phi^{r=R} \end{cases} $
Le problème étant caractérisé par une symétrie de révolution, l'équation se transforme telle que : $ \phi_{rr} = \frac{1}{r}\phi_{r} + k^2\phi = 0 $
On prendra les valeurs numériques suivantes $ R_{0} = 1m, R = 100m $ et $ k = 0.1m^{-1} $
[modifier] Résolution Analytique
On retrouve une équation du type Bessel traitée dans le cas 3, la solution est du type $ \phi(r) = AJ_{0}^{kr} + BY_{0}^{kr} \Rightarrow \phi_{r}^{r} = k(AJ_{1}^{kr} + BY_{1}^{kr}) $
En prenant, les conditions initiales : $ \begin{cases} \phi^{r=r_{0}} = AJ_{0}^{kr_{0}} + BY_{0}^{kr_{0}} = 1\\ \phi_{r}^{r=R} = -(kAJ_{1}^{kR} + kBY_{1}^{kR}) = ikAJ_{0}^{kR} + ikBY_{0}^{kR} \end{cases} $
On retrouve de la même manière que pour le cas 3 $ B = \frac{1-AJ_{0}^{kr_{0}}}{Y_{0}^{kr_{0}}} $ et $ A = -B\frac{ikY_{0}^{kR} + kY_{1}^{kR}}{ikJ_{0}^{kR} + kJ_{1}^{kR}} $
Après calcul on obtient $ B = \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})} $ et $ A = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})} $
Soit
$ \boxed{\phi(r) = - \frac{ikY_{0}^{kR} + kY_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})}J_{0}^{kr} + \frac{ikJ_{0}^{kR} + kJ_{1}^{kR}}{Y_{0}^{kr_{0}}(ikJ_{0}^{kR} + kJ_{1}^{kR}) + J_{0}^{kr_{0}} (ikY_{0}^{kR} + kY_{1}^{kR})}Y_{0}^{kr}} $
[modifier] Résolution par homotopie
On part de l’équation d’homotopie suivante $ (1-p)\phi_{rr} + p\phi_{rr} + \frac{1}{r}\phi_{r} + k^2\phi = 0 $
[modifier] Ordre 0
On reprend les mêmes conditions que précédemment telles que $ \phi_{0,rr} = 0 $ ce qui implique $ \phi_{0} = Ar + B $
Conditions aux limites : $ \begin{cases} \phi^{r_{0}} = 1 = Ar{0} + B\\ \phi_{r}^{R} = A = ik(AR + B) \Rightarrow \ A = \frac{ik}{1 - ikR}B \end{cases} $
Après résolution, on obtient $ B = \frac{1 - ikR}{1 + ik(r_{0} - R)} $ et $ A = \frac{ik}{1 + ik(r_{0} - R)} $
Au final pour l’ordre 0 $ \boxed{\phi_{0}(r) = \frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}} $
[modifier] Ordre 1
On reprend l’équation générale d’homotopie pour un ordre 1, on trouve $ \phi_{1,rr} + \frac{1}{r} \phi_{0,r} + k^2\phi_{0} = 0 $
Soit $ \phi_{1,rr} = - \frac{1}{r} (\frac{ik}{1 + ik(r_{0} - R)}) - k^2 (\frac{ik}{1 + ik(r_{0} - R)} r + \frac{1 - ikR}{1 + ik(r_{0} - R)}) $
$ \Rightarrow \phi_{1,r} = -ln(r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} r^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} r + C_{1} $
$ \Rightarrow \phi_{1} = - (r ln(r) - r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r^2 + C_{1}r + C_{2} $
Conditions aux limites : $ \begin{cases} \phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r_{0}^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{2} \frac{ik}{1 + ik(r_{0} - R)} R^2 - k^2 \frac{1 - ikR}{1 + ik(r_{0} - R)} R + C_{1} = -ik (R ln(R) - R) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} R^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} R^2 + C_{1}R + C_{2} \end{cases} $
En reprenant les notations à l'ordre à pour $ A $ et $ B $, on a
$ \begin{cases}\phi_{1}^{r_{0}} = 1 = - (r_{0} ln(r_{0}) - r_{0}) A - \frac{k^2}{6} A r_{0}^3 - \frac{k^2}{2} B r_{0}^2 + C_{1}r_{0} + C_{2}\\ \phi_{1,r}^{R} = -ln(R) A - \frac{k^2}{2} A R^2 - k^2 B R + C_{1} = -ik (R ln(R) - R) A - \frac{k^2}{6} A R^3 - \frac{k^2}{2}B R^2 + C_{1}R + C_{2} \end{cases} $
Après calcul, on trouve les constantes suivantes $ \begin{cases} C_1=(6Ar_{0}ln(r_{0})+3Bk^{2}r_{0}^{2}-6Ar_{0}+(-AR^{3}-3BR^{2}+(6B+3A)R+Ar_{0}^{3})k^{2}+AR\frac{(6i-6iln(R))k+6Aln(R)+6)}{6} \\C_2=-(6AR-6A)r_{0}ln(r_{0})+(3BR-3B)k^{2}r^{2}+(6A-6AR)r_{0}+(-AR^{4}-3BR^{3}+(6B+3A)R^{2}+Ar^{3}R-Ar^{3})k^{2}+AR^{2}\frac{(6i-6iln(R))k+R(6Aln(R)+6)-6)}{6} \end{cases} $
Finalement on a bien $ \boxed{\phi_{1}(x) = - (r ln(r) - r) \frac{ik}{1 + ik(r_{0} - R)} - \frac{k^2}{6} \frac{ik}{1 + ik(r_{0} - R)} r^3 - \frac{k^2}{2} \frac{1 - ikR}{1 + ik(r_{0} - R)} r^2 + C_{1}r + C_{2}} $
[modifier] Proposition d’application
L’homotopie appliquée a l’équation de Berkhoff permet de modéliser et de prévoir l’impact de la houle sur les littoraux, de manière plus ou moins précise. Cette méthode s’applique à la houle, mais elle peut aussi être utile dans la modélisation d’autres phénomènes complexes qui mettent en jeu la propagation d’ondes. On voit nettement l’utilité de cette méthode et son application concrète sur les littoraux. En anticipant l’impact de la houle sur la côte, on est capable de bâtir des infrastructures spécifiques adaptées à chaque littoral, pour réduire l’érosion et ralentir les effets du réchauffement climatique sur ces espaces protégés et caractériels que sont les littoraux.
Pour illustration, on peut d’après les études de propagation de la houle choisir le type de digue adapté pour réduire l’énergie des vagues lorsqu'elles se fracassent sur le littoral:
Voici une vidéo qui résume et vulgarise le projet :
 S'abonner à un flux RSS
S'abonner à un flux RSS