Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/BRISSET - DOUILLARD JACQ - LESNE

Contexte

Le changement climatique est global, mais touchera de manière différenciée les différentes régions et espaces du monde (côtes, montagnes, villes,…). Le Conservatoire du littoral, en tant que propriétaire des espaces naturels littoraux qu'il protège, participe à la réflexion sur la gestion raisonnée et durable des littoraux qui contribue à l’adaptation au changement climatique. On constate actuellement une accélération de l’augmentation du niveau de la mer due au changement climatique. Dans ce projet, nous chercherons à modéliser l'impact du changement climatique sur le littoral.

• 

  Les Sables d'Olonne

• 

  Calanque entre Cassis et Marseille

Au cours de ce projet, il s'agira donc de quantifier les conséquences du changement climatique sur la modification des conditions de propagation des houles à la côte et sur l'inondabilité des côtes et des berges des estuaires. Les méthodes analytiques, appliquées sur l'équation des ondes et les équations de Berkhoff, permettront de reproduire la déformation des vagues par petits fonds.

Nous allons donc étudier différents cas, dans lesquels nous exposerons : une solution analytique, une solution semi-analytique (homotopie, une superposition de la solution analytique et de la solution par homotopie, une étude de sensibilité de la solution en fonction du nombre d'onde, ainsi qu'une réflexion portant sur l'analyse des résultats, les limites et l'intérêt de la méthode d'homotopie.

Le modèle de Berkhoff

Dans le but de modéliser la houle, nous allons utiliser le modèle de Berkhoff. Ce modèle est utilisé pour anticiper les phénomènes sur la propagation et l'impact des vagues sur les côtes.

C'est un modèle bi-dimensionnel qui a pour expression:

$ \nabla(CC_{g}\nabla(Φ))+k^{2}CC_gΦ=0 $

On note:

ϕ : le potentiel de vitesse C : la célérité de l'onde Cg : la célérité de groupe des vagues k : le nombre d'onde

Ce modèle se base sur un grand nombre d'hypothèses:

- le fluide est considéré conne étant parfait, incompressible et irrotationnel

- le fond est fixe et imperméable

- la hauteur de la houle est faible par rapport à sa longueur d’onde et à la profondeur

- on néglige les sollicitations atmosphériques à la surface libre

Nous nous plaçons dans le cadre des ondes longues, ce qui signifie que C = Cg = $ \sqrt{gH} $.

L'équation devient alors:

$ \frac{\partial^2 Φ}{\partial x^2} + k^{2}Φ=0 $

L'évolution dans le temps de la hauteur de houle est donnée par : $ \color{red}h(x,t)=R(ϕe^{−iωt}) $.

Etudes des différents cas

Cas n°1

Dans un premier temps, nous allons considérer un domaine unidimensionnel à fond plat de longueur L avec l'entrée en aval d'une onde unitaire ϕ=1 et avec la sortie libre de cette onde en amont caractérisée par la condition à la limite en x = L : $ \frac{\partial Φ}{\partial x} = ikΦ $ soit $ Φ_{x} (x = L) = ikΦ(x = L) $

Résolution analytique

On obtient une équation homogène à coefficients constants que l'on va chercher à résoudre. L'équation peut se réécrire : $ Φ_{xx} +k^{2}Φ=0. $

Première étape : Equation caractéristique

$ X^{2} +k^{2} =0 $ ⟺ $ X = ± ik $

Deuxième étape : Résolution de l'équation

On cherche alors une résolution de Φ sous la forme $ Φ(x)= Acos(kx) + Bsin(kx) $

Condition aux limites :

$ Φ(0) = A = 1 $

$ Φ_{x} (x = L) = ikΦ(x = L) $

⟺ $ -ksin(kL) + Bcos (kL) = ik(cos(kL) + Bsin(kL)) $ ⟺ $ B = \frac{sin(kL)+icos(kL)}{cos(kL)-isin(kL)} $

Ainsi, on obtient $ Φ(x) = $ $ \cos (kx) + $ $ \frac{sin(kL)+icos(kL)}{cos(kL)-isin(kL)} sin (kx) $

On peut ensuite déterminer la hauteur de houle est donnée par : $ h(x,t)=R(ϕe^{−iωt}) $. En multipliant le second terme dans le formule de Φ par son conjugué, et en effectuant les simplifications nécessaires, on obtient rapidement

$ \color{red} Φ(x) = cos(kx) + isin (kx) $, donc $ \color{red}Φ(x) = e^{ikx} $

Or, $ R(Φ) = cos (kx) $

Donc $ \color{blue}h(x,t) = cos (kx-wt) $

Résolution avec la méthode de l'homotopie

La relation d'homotopie est donnée par : $ Φ_{xx}(1-p)+p(Φ_{xx}+k^{2}Φ)=0 $

• A l'ordre 0 :

$ Φ_{0,xx}=0 $

Ainsi, $ Φ_{0}(x)= Ax + B $

Conditions aux limites :

$ Φ(0) = B = 1 $

$ Φ_{x} (x = L) = ikΦ(x = L) $ ⟺ $ A = ik(AL +1) $ ⟺ $ A = $$ \frac{ik}{1 - ikL} $

Donc $ \color{red}Φ_{0}(x)= \frac{ik}{1 - ikL}x + 1 $

• A l'ordre 1 :

$ Φ_{1,xx} + k^{2}Φ_{0} $ = 0

On a alors donc, grâce aux conditions aux limites imposées :

$ B = \frac{-1}{k^{2}} $

$ A = $$ (\frac{ik}{1 - ikL})(\frac{L^{2}}{2}-\frac{L^{3}}{6}) + \frac{1}{k^{2}} + L - \frac{L^{2}}{2} $

Ordre N : $ ϕ_{N,xx}+k^{2}ϕ_{N−1}=0 $

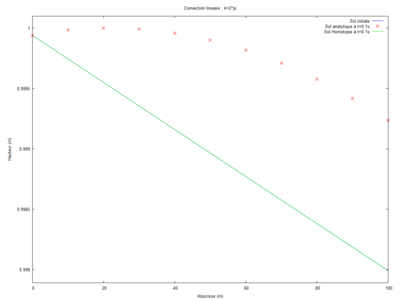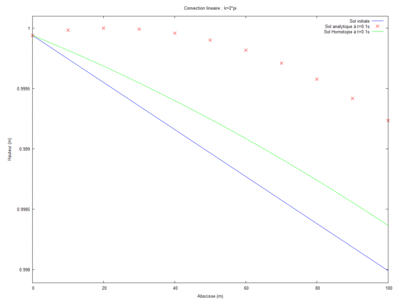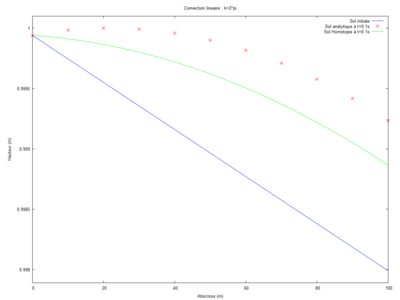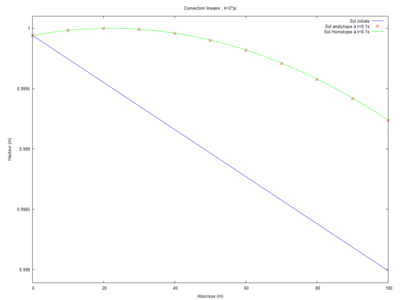
Superposition de la solution analytique et de la solution par homotopie

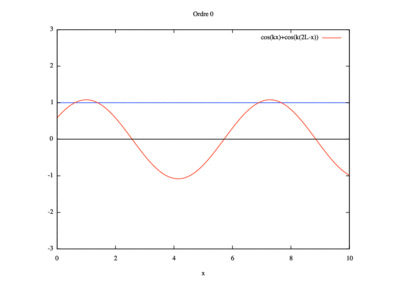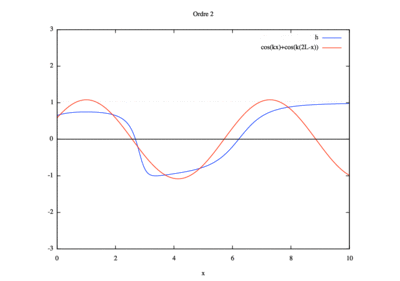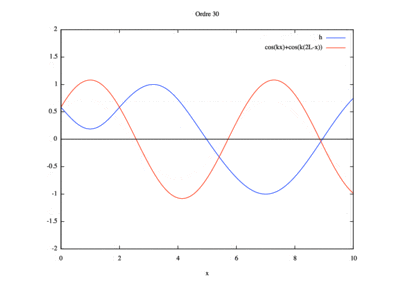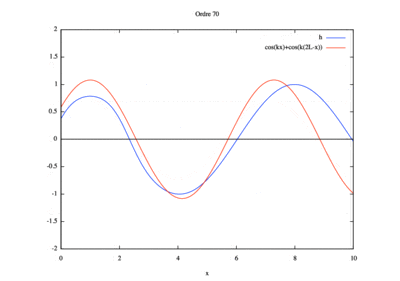
Pour réaliser cette simulation, nous avons étudié les différents ordres. Nous sommes parti de l'ordre 0 puis nous avons chercher pour quel ordre la solution homotopique convergeait vers la solution analytique. Il nous a fallu ainsi 13 ordre pour observer cette convergence.

Etude de sensibilité de la solution en fonction du nombre d'onde et analyse des résultats

Le modèle de Berkhoff a permis de tracer l'évolution de la hauteur des vagues en fonction du temps. Les différents modèles montrent que la houle est régulière quelque soit les paramètres du fond.

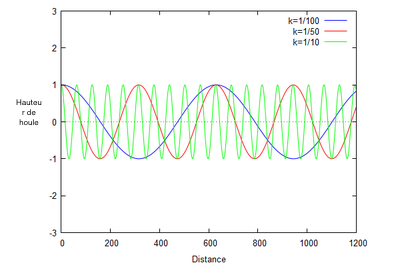
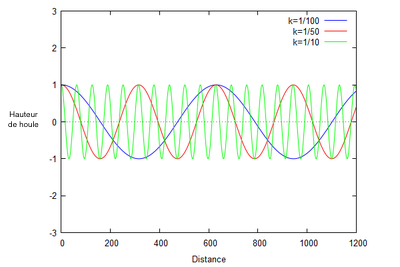
Dans cette section, nous allons étudier l'impact de la période sur la hauteur de la houle. Tout d'abord, ce facteur repose sur les conditions météorologiques. La période représente, en seconde, le temps que met une onde pour passer par le même état vibratoire : soit le temps d'une crête à la suivante.Grâce à l'animation, nous observons que, lorsque la période augmente, la fréquence des vagues diminue et les vagues apparaissent de manière moins régulière.

On remarque également que la hauteur de la houle n'est pas impacté par la période. Cela peut s'expliquer par le fait que les vagues transportent de l'énergie proportionellement à la période de la houle. De ce fait, elles s'atténuent au fur et à mesure en raison d'une dissipation d'énergie. A contrario,les vagues ayant une période longue se déplacent plus vite et parcourt donc des distances plus longues. Ce sont ces vagues qui vont avoir un impact considérable pour nos littoraux.

Les approximations que nous avons effectués afin d'obtenir un modèle plus simpliste nous éloigne de la réalité de l'impact de la houle sur les littoraux. De manière général, nous avons négligés : les courants marins, les marées, l' interaction des vagues entre elles et bien d'autres encore...

Dans le cas 1 :

k = $ \frac{2pi}{T} $

Limite de la méthode d'homotopie

Nous avons vu dans l'introduction qu'une houle était caractérisée par une amplitude, une période, une longueur d'onde et une direction. En réalité cela s'avère plus complexe. Une onde n'est jamais monochromatique, elle est composée de train de vagues et de périodes diffférentes, or la méthode par homotopie ne peut pas prendre en compte ces autres paramètres. Les hypothèses effectuées au-dessus, comme un fond plat, ne réflètent pas la réalité des littoraux mais permet d'en approcher un modèle sensiblement proche. De plus l'échelle adoptée ne premet d'obtenir une solution très précise dans le cas 1.

Cas n°2

Dans ce second cas, on se place en domaine unidimensionnel avec un fond plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ ϕ_{x}=ik(2−ϕ) $ et une réflexion totale en amont $ ϕ_{x}=0 $.

Résolution analytique

Les conditions aux limites deviennent alors :

En Aval pour x = 0 : $ ϕ_{x}=ik(2−ϕ) $

En Amont pour x = L: $ ϕ_{x}=0 $

En reprenant l'équation de Berkhoff simplifiée, on cherche alors a résoudre $ ϕ_{xx}+k^{2}ϕ=0 $

Première étape : Equation caractéristique

$ X^{2} +k^{2} =0 $ ⟺ $ X = ± ik $

Deuxième étape : Résolution de l'équation

On cherche alors une résolution de Φ sous la forme $ Φ(x)= Ae^{ikx}+Be^{-ikx} $

Condition aux limites : ∙ En aval (x = 0): $ ϕ_{x}=ik(2−ϕ) ⟺ A = 1 $

∙ En amont (x = L) : $ ϕ_{x}= 0 ⟺ B = e^{2ikL} $

On en déduit l'expression de ϕ :

$ \color{red}ϕ(x)=e^{ik(2L−x)}+e^{ikx}=cos(2kl−kx)+isin(2kL−kx)+cos(kx)+isin(kx) $

La hauteur de la houle est donc donnée par la relation : $ \color{blue}h(x,t)=(cos(2kl−kx)+cos(kx))cos(wt) $

Résolution avec la méthode de l'homotopie

La relation d'homotopie est la même que pour le cas n°1, seules les conditions initiales diffèrent (comme vu plus haut).

• A l'ordre 0 :

$ Φ_{0,xx}=0 $

Ainsi, $ Φ_{0}(x)= Ax + B $

Condition aux limites : ∙ En aval (x = 0): $ ϕ_{x}=ik(2−ϕ) $

∙ En amont (x = L) : $ ϕ_{x}= 0 $

On obtient alors de façon immédiate avec la 2ème condition au limite A = 0

On en deduit avec la première condituion aux limites que B = 2

Donc $ \color{red}Φ_{0}(x) = 2 $

• A l'ordre 1 :

$ Φ_{1,xx} + k^{2}Φ_{0} $ = 0

On a alors $ Φ_{1}(x)= -k^{2}x^{2} + Ax + B $

Avec les contions initiales, on obtient alors :

$ A = 2k^{2}L $

$ B = 2ikL $

On aboutit donc à l'équation suivante : $ \color{red}ϕ_{1}(x)=-k^{2}x^{2} + 2k^{2}Lx + 2ikL $

Superposition de la solution analytique et de la solution par homotopie

Pour réaliser cette simulation, nous avons étudié les différents ordres. Nous sommes parti de l'ordre 0 puis nous avons chercher pour quel ordre la solution homotopique convergeait vers la solution analytique. Il nous a fallu ainsi 12 ordre pour observer cette convergence.

Convergence de la solution homotopique vers la solution analytique de l'odre 0 à l'odre 12 :

Etude de sensibilité de la solution en fonction du nombre d'onde

Analyse des résultats

Le phénomène de battement permet de caractériser les noeuds et les ventres de l'onde.

L'analyse de sensibilité nous a permis de changer k, avec kL inférieur à 1, c'est à dire qu'on a pu faire varier k avec L constant. Lorsque k augmente, c'est à dire lorsque le nombre d'ondes par mètre augmente alors $ \lambda $ diminue ainsi que la période T.

Limite de la méthode d'homotopie

Comme dans le cas 1, les hypothèses sur l'unidimentionnalité de l'onde et le fond plat nous donne un modèle approché car en réalité l'onde est tridimentionnelle et les fonds marins sont de profondeurs variables. En effet la complexité de ces paramètres seraient difficile à modéliser, en raison de leur grande varaiabilité en fonction des diiférentes zones étudiées.

Cas 3 : Domaine monodimensionnel de longueur L avec pente du fond constante (s=cste) avec entrée par l'aval d'une onde de fréquence unitaire ϕ=1 et sortie libre amont ϕx=ikϕ

Résolution analytique

Dans le cas numéro 3, la résolution analytique s'avère être plus complexe. En effet, H n'est plus une constante mais dépend de la longueur du système x et de la pente s :

$ H(x)= H_0-sx $

De plus, les conditions aux limites sont les suivantes :

$ Φ(0)= 1 $

$ Φ_{x} (x = L) = ikΦ(x = L) $

$ CC_g=gH(x) $

Dès lors, l'équation de Berkhoff précédente :

$ \nabla(CC_{g}\nabla(Φ))+k^{2}CC_gΦ=0 $ (*) devient :

$ H\frac{\partial^2 Φ}{\partial x^2} + \frac{\partial H}{\partial x}\frac{\partial Φ}{\partial x} + k^2HΦ =0, x\in[0,L] $

Deuxième étape : Obtention de l'équation

Nous cherchons à mettre notre équation sous forme de Bessel telle que :

$ H\frac{\partial^2 Φ}{\partial x^2} + \frac{\partial H}{\partial x}\frac{\partial Φ}{\partial x} + k^2HΦ =0 $

Prenne la forme :

$ x^2\frac{\partial^2 Φ}{\partial x^2} + x\frac{\partial Φ}{\partial x} + x^2Φ =0 $

Dès lors, posons $ \varphi(y)= \frac{k}{s}(H_o-sy) $, $ y\in[\frac{k}{s}H_o, \frac{k}{s}(H_o-sL)] $. $ \varphi $ est $ C^2 $ et $ bijective $ car la fonction est affine.

On peut donc opérer le changement de variable $ z =\frac{k}{s}(H_0-sx) $, dès lors :

$ zsk\frac{\partial^2 Φ}{\partial z^2} + sk\frac{\partial Φ}{\partial z} + zskΦ =0 $

ssi $ z^2\frac{\partial^2 Φ}{\partial z^2} + z\frac{\partial Φ}{\partial z} + z^2Φ =0 $,

On obtient bien une équation différentielle de Bessel.

Troisième étape : Résolution de l'équation générale

Notre équation est sous forme canonique, la théorie nous dit alors que le plan de solutions est de la forme suivante : $ Φ(z) = AJ_0(\sqrt{\frac{k}{s}(H_o-sx)})+BY_0(\sqrt{\frac{k}{s}(H_o-sx)}) $ avec $ J_0 $ la fonction solution de Bessel définie en 0 et $ Y_0 $ la fonction solution de Bessel non définie en 0.

Dernière étape : Détermination des constantes avec l'aide des conditions aux limites

Pour rappel :

$ Φ(0)= 1 $

$ Φ_{x} (x = L) = ikΦ(x = L) $

Dans notre cas, puisque $ z=\frac{k}{s}(H_o-sx) $, on a :

$ \varphi(x=0)= \frac{k}{s}H_o $

$ Φ_{x} (x = L)= ikΦ(x = L) $

Alors : $ Φ(0) = AJ_0(\sqrt{\frac{k}{s}H_o})+BY_0(\sqrt{\frac{k}{s}H_o})) $ = 1

On notera $ z_0 = \sqrt{\frac{k}{s}H_o} $.

De plus, $ Φ_x(L)= ik(AJ_0(\sqrt{\frac{k}{s}(H_o-sL)})+BY_0(\sqrt{\frac{k}{s}(H_o-sL)}) $

Et $ Φ_x(L)= k(AJ_1(\sqrt{\frac{k}{s}(H_o-sL)})+BY_1(\sqrt{\frac{k}{s}(H_o-sL)}) $

En effet, $ J_0'=-J_1 $. On notera $ z_L=\sqrt{\frac{k}{s}(H_o-sL)} $

Dès lors :

$ AJ_0(z_0)+BY_0(z_0) = 1 $ (1)

$ i(AJ_0(z_L)+BY_0(z_L))= (AJ_1(z_L)+BY_1(z_L) $ (2)

ssi $ AJ_0(z_0)+BY_0(z_0) = 1 $ (1)

$ iAJ_0(z_L)+iBY_0(z_L)= AJ_1(z_L)+BY_1(z_L) $ (2)

ssi $ AJ_0(z_0)+BY_0(z_0) = 1 $ (1)

$ A = B\frac{iY_0(z_L)-Y_1(z_L)}{J_1(z_L)-iJ_0(z_L)} $ (2)

En injectant (2) dans (1), on obtient :

$ B = \frac{1}{Y_0(z_0)+J_0(z_0)\frac{iY_0(z_L)-Y_1(z_L)}{J_1(z_L)-iJ_0(z_L)}} $

De manière analogue : $ A = \frac{iY_0(z_L)-Y_1(z_L)}{Y_0(z_0)(J_1(z_L)-iJ_0(z_L))+J_0(z_0)(iY_0(z_L)-Y_1(z_L))} $

On a donc la solution analytique suivante :

$ Φ(z) = AJ_0(\sqrt{\frac{k}{s}(H_o-sx)})+BY_0(\sqrt{\frac{k}{s}(H_o-sx)}) $ avec $ x\in[0,L] $

Résolution avec la méthode d'homotopie

On a également les relation suivantes, déterminées par la relation d'homotopie :

- $ \phi=\sum_{k=0}^\infty p^n \phi_n $

- La 1ère dérivée $ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $

- La seconde dérivée $ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $

Pour l'ordre 0 :

A l'ordre 0, on obtient l'équation suivante : $ \phi_{0,xx}= 0 $

Ainsi, $ Φ_{0}(x)= Ax + B $

Les conditions initiales sont les suivantes :

$ \bullet x=0, \phi(x=0)=1 $

donc on obtient $ B= 1 $

$ \bullet x=L, \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(x=L) $ donc $ A=\frac{ik}{1-ikL} $

On obtient la solution finale suivante : $ \phi_0(x)=1+\frac{ik}{1-ikL}x $

Ordre 1 :

L'équation devient à l'ordre 1 :

$ \phi_{1,xx}-\phi_{0,xx}+(H_0-sx)\phi_{0,xx}-s\phi_{0,x}+k^2(H_0-sx)\phi_0=0 $
c'est-à-dire $ \phi_{1,xx}-s\phi_{0,x}+k^2(H_0-sx)\phi_0=0 $

On intègre ensuite deux fois l'expression de $ \phi_0 $ pour obtenir $ \phi_1 $ avec les conditions aux limites $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $

On réitère ensuite ce procédé pour les ordres supérieurs.

Cas n°4 : Domaine monodimensionnel de longueur L avec pente du fond exponentielle et sortie libre amont

Résolution : Méthode analytique

Pour le cas 4, on a comme expression pour la hauteur

$ H(x)=H_0\mathrm{e}^{-sx} $

L'équation de Berkhoff devient donc : $ H_0\mathrm{e}^{-sx}\frac{\partial^2\phi}{\partial x^2}-sH_0\mathrm{e}^{-sx}\frac{\partial\phi}{\partial x}+k^2H_0\mathrm{e}^{-sx}\phi=0 $

En factorisant l'expression précédente on obtient : $ H_0\mathrm{e}^{-sx}\Big(\frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k^2\phi\Bigr)=0 $

Or, on sait que $ H_0\mathrm{e}^{-sx}\neq0 $

Donc on peut écrire la relation suivante : $ \frac{\partial^2\phi}{\partial x^2}-s\frac{\partial\phi}{\partial x}+k^2\phi=0 $

L'équation caractéristique associée est donc : $ x^2-sx+k^2=0 $

On va ensuite examiner les 3 cas différents, celle pour lequel le discriminant est positif, celle pour lequel il est nul et celle pour lequel il est négatif : $ \Delta=s^2-4k^2 $

Si $ \Delta<0 $; l'équation est de la forme :$ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[A_1\cos\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)+A_2\sin\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)] $

Si $ \Delta=0 $; l'équation est de la forme : $ \phi(x)=(A_1x+A_2)\mathrm{e}^{\frac{s}{2}x} $

Si $ \Delta>0 $ ; l'équation est de la forme : $ \phi(x)=A_1\mathrm{e}^{\frac{s-\sqrt{s^2-4k^2}}{2}x}+A_2\mathrm{e}^{\frac{s+\sqrt{s^2-4k^2}}{2}x} $

Avec les conditions initiales, on va chercher à exprimer les 2 constantes $ A_1 $ et $ A_2 $ :

$ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(x=L)=ik\phi(L) $

1er cas: Si $ \Delta<0 $ : on note $ σ=\frac{\sqrt{s^2-4k^2}}{2} $

$ A_1=1 $ et $ A_2=\frac{σ\sin(σL)+\cos(σL)(ik-1)}{σ\cos(σL)+\sin(σL)(1-ik)} $

L'équation s'écrit : $ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[\cos\Big(σx\Bigr)+\frac{σ\sin(σL)+\cos(σL)(ik-1)}{σ\cos(σL)+\sin(σL)(1-ik)}\sin\Big(σx\Bigr)] $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

Pour tracer les courbes, nous avons pris comme valeurs numériques :

T=2s

H0=2m

k=0.709m−1

c=4.43m/s

s=0.01

• 

2ème cas : Si $ \Delta=0 $ :

$ A_1=\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL} $ et $ A_2=1 $

L'équation s'écrit : $ \phi(x)=(\frac{ik-\frac{s}{2}}{1-\frac{s}{2}L-ikL}x+1)\mathrm{e}^{\frac{s}{2}x} $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

s=1.418

k=0.709m−1

c=4.43m/s

T=2s

H0=2m

• 

3ème cas : Si $ \Delta>0 $ :

on note $ x_1=\frac{s-\sqrt{s^2-4k^2}}{2} $ et $ x_2=\frac{s+\sqrt{s^2-4k^2}}{2} $

$ A_1=1-\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}} $ et $ A_2=\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}} $

L'équation s'écrit : $ \phi(x)=\Big(1-\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}}\Bigr)\mathrm{e}^{\frac{s-\sqrt{s^2-4k^2}}{2}x}+\frac{ik\mathrm{e}^{x_1L}-x_1\mathrm{e}^{x_1L}}{x_2\mathrm{e}^{x_2L}-x_1\mathrm{e}^{x_1L}+ik\mathrm{e}^{x_1L}-ik\mathrm{e}^{x_2L}}\mathrm{e}^{\frac{s+\sqrt{s^2-4k^2}}{2}x} $

Expression de la hauteur : $ H= \frac{Re(\phi)}{|\phi|} $

s=2

k=0.709m−1

c=4.43m/s

T=2s

H0=2m

• 

Résolution par la méthode homotopique

L'équation homotopique pour le cas 4 est : $ (1-p)\phi_{xx}+p(\phi_{xx}-s\phi_x+k^2\phi)=0 $

$ \phi=\sum_{k=0}^\infty p^n \phi_n $

$ \phi_{x}=\sum_{k=0}^\infty p^n \phi_{n,x} $

$ \phi_{xx}=\sum_{k=0}^\infty p^n \phi_{n,xx} $

Ordre 0 : $ \phi_{0,xx}=0 $

Ordre 1 : $ \phi_{1,xx}-s\phi_{0,x}+k^2\phi_0=0 $

Ordre 2 : $ \phi_{2,xx}-s\phi_{1,x}+k^2\phi_1=0 $

Ainsi, à l'Ordre N : $ \phi_{N,xx}-s\phi_{N-1,x}+k^2\phi_{N-1}=0 $

Analyse des résultats et limites du modèle

Le modèle de Berkhoff utilisé pour ce projet nous a permis de faire l'étude de l'évolution de la hauteur des vagues en fonction de distance x. Les différents modèles établi montrent que la houle est plutôt constante dans le cas 1, le cas 2 et le cas 3. Pour le cas 4 on remarque une hauteur de vague qui finit par tendre vers 0 pour $ \Delta<0 $ et $ \Delta=0 $;. On peut donc conclure que pour le cas n°4, seul le cas ou delta est négatif reste physiquement acceptable.

Le modèle permet d'observer qualitativement les cambrures des vagues selon les différents cas. Il permet aussi d'analyser l'influence de la période T de la houle sur les côtes. En effet, la houle transporte de l'énergie qui est proportionnelle à sa période, ce qui permet de déterminer son impact sur les côtes.

Nous pouvons cependant émettre quelques limites quant aux différents cas étudies. Dans un premier temps, nous nous sommes placés dans un domaine monodimensionnel. Or le modèle de Berkhoff est bidirectionnel. Il aurait donc fallu se placer dans domaine bidirectionnel pour s'approcher davantage de la réalité.

De plus, le modèle de Berkhoff nécessite de nombreuses hypothèses simplificatrices que nous rappelons :

- le fluide est considéré comme étant parfait, incompressible et irrotationnel

- le fond est fixe et imperméable

- la hauteur de la houle est faible par rapport à sa longueur d’onde et à la profondeur

- on néglige les sollicitations atmosphériques à la surface libre

Dans le but d'améliorer le modèle, il serait dont pertinent d'étudier la vitesse, la durée du vent, l'état d'origine à la surface de la mer et également considéré que le fluide n'est pas un fluide parfait.

Application à l'aménagement des littoraux pour lutter contre l'érosion

La houle est le phénomène physique causant l'érosion des littoraux. La prédiction et la modélisation des phénomènes de houles permet d'anticiper le phénomène d'érosion des littoraux et de les aménager en conséquence.

Afin de lutter contre ce phénomène d'érosion il existe divers méthodes mises en place sur les littoraux français : les méthodes dites "dures" (épis, digues, perrés, brises-lames etc) et les méthodes dites "douces". Les méthodes « douces » sont conçues pour « travailler avec la nature » en intégrant la dynamique naturelle du littoral et la mobilité du trait de côte (rechargements de la plage en sédiment, travail sur la végétalisation, etc.).

Epis retenant les galais en Baie de Somme (méthode dure)

Les ouvrages géotextiles visent à maintenir le sable et peuvent être déployés perpendiculairement.Ils sont constitués de toiles perméables en fibres synthétiques sous forme de sacs ou de boudins. Ils sont remplis de sable par une pompe refoulante. Ils ont l'avantage de peu perturber l’écosystème littoral, ils s'intègrent donc dans une démarche plus durable et respectueuse de l'environnement.

Ouvrage en géotextiles (méthode douce)

Les enjeux climatiques sont importantqs quant à l'érosion des littoraux en effet le réchauffement climatique augmente le niveau de la mer ce qui contribue à accentuer le phéomène de houle et par conséquent l'érsion des littoraux.