Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/RIEG - TOISOUL - YVINEC

Groupe Joséphine RIEG, Morgane TOISOUL et Lisa YVINEC

Introduction

L’élévation du niveau de la mer actuelle est l'augmentation du niveau moyen des océans en cours depuis le début du XXe siècle. C'est une conséquence du réchauffement climatique, il est principalement dû à la fonte des glaces terrestres et à la dilatation thermique des océans. Le niveau de la mer a augmenté de 0,16 m entre 1902 et 20154 et le phénomène s'est accéléré ces dernières années. Ainsi, quelque 824 millions de personnes à l’horizon 2030, et 1,2 milliard en 2060, seraient menacées par la montée des eaux.

Le sillon de Saint-Malo.

L'objectif de ce travail est d'évaluer l'impact des vagues en lien avec la montée des eaux, susceptibles de détruire des ouvrages et habitations humaines.

Pour cela, nous modéliserons les houles, en utilisant le modèle de Berkhoff, une équation aux dérivées partielles, que nous résoudrons par une méthode analytique puis par homotopie, dans l'hypothèse d'ondes longues et en étudiant différents cas concrets de géométries et de conditions aux limites.

Cas n°1 : Canal monodimensionnel plat avec sortie libre

On part d'une solution initiale nulle. En choisissant la dérivée seconde comme fonction auxiliaire linéaire on obtient le problème suivant : $ (1-p)\phi_{xx} + p(\phi_{xx}+k^2\phi) = 0 $

Solution analytique

On peut simplifier les calculs et résoudre une équation différentielle de second ordre du type : $ X^2 + k^2 = 0 $

Discriminant : $ Δ = -4k² $ → $ X1=-ik $ et $ X2=+ik $

Donc la solution sera de la forme : $ Φ(x)=A \text{e}^{-ikx}+B \text{e}^{ikx} $, avec A,B réels

Déterminons A et B avec les conditions limites :

$ Φ(x=0)=1 $ → $ A+B=1 $

$ Φ’(x=0)=ikΦ $ → $ B=0 $ → $ A=1 $

Conclusion : $ \color{NavyBlue} {Φ(x)=\text{e}^{ikx}} $

Maintenant que l'on a le potentiel des vitesses Φ, on va déterminer h qui est la hauteur d'eau algébrique s'ajoutant à la hauteur d'eau moyenne H constante dans ce Cas n°1.

L'évolution dans le temps de la hauteur de houle est donnée par : $ h(x,t)=\Re(Φ\text{e}^{-iωt}) $

$ Φ(x,t)=\text{e}^{i(kx−ωt)} $ or $ H=\Re(ϕ) $

Conclusion : $ \color{NavyBlue} {h(x,t)=\cos(kx-ωt)} $

Solution par la méthode d'homotopie

Avec la méthode d'homotopie, on peut décomposer le problème comme suit : $ (1-p)\phi_{xx} + p(\phi_{xx}+k^2\phi) = 0 $
avec une décomposition en série entière : $ ϕ(x,p)=ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $

Dans un premier temps on réinjecte ϕ dans la relation d'homotopie et on résout l'équation en fonction des puissances de p croissantes.

Ordre 0

$ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :

$ \color{NavyBlue}\phi_0=1+\dfrac{ik}{1-ikL}x $.

Ordre 1

$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $, il vient : $ \phi_1=- \dfrac{k^2L(k^2L^2+3ikL-3)} {3(1-ikL)^2}x-k^2\left (\dfrac{ik} {6(1-ikL)}x^3+\dfrac{1} {2}x^2 \right ) $

A l'ordre 1, la solution est donc : $ \color{NavyBlue} ϕ(x,p)=ϕ_0(x)+pϕ_1(x) $

Ordre 2

A l'aide de Maxima cette fois-ci on résout l'équation d'ordre 2: $ \phi_{2,xx}-\phi_{1,xx}+\phi_{1,xx}+k^2\phi_1=0 $ soit $ \phi_{2}=-k^2\int\phi_1dxdx +Ax+B $.

Grâce aux conditions limites on déduit $ \phi_{2} $. L'expression est beaucoup trop longue pour la déposer sur cette page.

Ordres supérieurs

On itère le processus pour déterminer les $ \phi_i $

On en déduit ensuite la hauteur de la houle $ \color{NavyBlue} h(x,t)=R(Φ\text{e}^{-iωt}) $

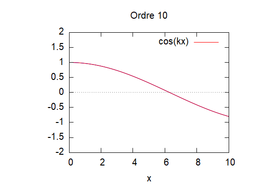
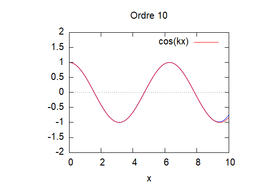
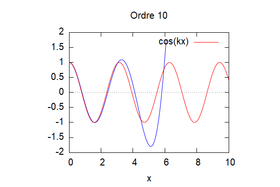
Voici les solutions approchées pour chaque ordre avec K=1 et L=1/K (pour pouvoir simplifier les calculs) et à t=0 pour p=1:

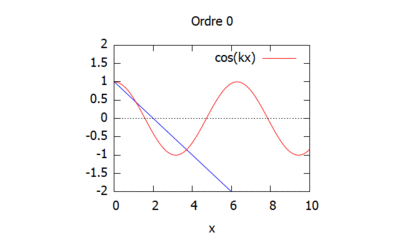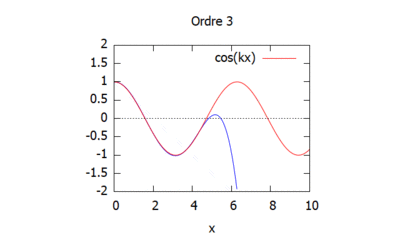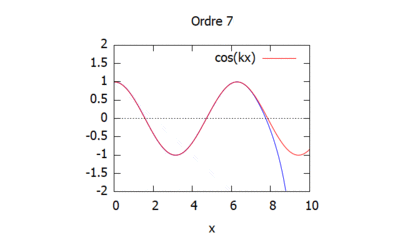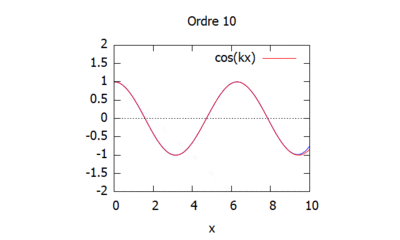
On remarque grâce à cette visualisation que plus les ordres augmentent, plus la méthode d'homotopie (ici en bleu) vient s'approcher de la solution théorique (ici en rouge). Ainsi, la solution par homotopie converge vers la solution analytique.

Sensibilité de la solution en fonction du nombre d'onde

Voici l'analyse de la sensibilité pour le cas n°1 au niveau des solutions homotopiques. Pour cela, nous avons fait varier la valeur de k et on observe (voir les images suivantes) que plus k est petit plus la solution homotopique (ici en bleu) converge vite vers la solution analytique.

k=0.25

k=1

k=2

Cas n°2 : Canal monodimensionnel plat avec réflexion totale en amont

Cette fois on se place dans le cas monodimensionnel avec une réflexion totale en amont $ ϕ_x=0 $ et une condition de flux aval : $ ϕ_x=ik(2−ϕ) $
Le problème est toujours le même : $ (1-p)\phi_{xx} + p(\phi_{xx}+k^2\phi) = 0 $
avec les nouvelles conditions aux limites.

Solution analytique

On simplifie l'équation du problème et on résout la même équation caractéristique que pour le cas 1 : $ X^2 + k^2 = 0 $

La solution reste de la forme $ Ae^{-ikx}+ Be^{ikx} $, avec A et B des constantes complexes.

Déterminons A et B avec les conditions limites :

• $ Φ’(x=0)=0 $
• $ Φ’(x=L)=ik(2-Φ) $

On déduit alors :

• $ A=e^{2ikL} $
• $ B=1 $

Conclusion : $ \color{NavyBlue}{ϕ(x)=e^{ik(2L-x)}+e^{ikx}} $

A amplitude et phase nulles, la solution est simplifiée. Mais lorsqu'on ajoute une amplitude $ U $ et une phase $ \Phi $, la solution est inchangée.

D'où, $ \color{NavyBlue}{ϕ(x,t)=e^{i[k(2L-x)-\omega t]}+e^{i(kx-\omega t)}} $

Conclusion : La hauteur d'eau est : $ \color{NavyBlue}{h(x,t)=\Re(ϕ(x,t))=cos(k(2L-x)-\omega t)+cos(kx-\omega t)} $

Solution par homotopie

La résolution par homotopie est très similaire à celle du cas 1 : seules les condition initiales sont modifiées. Similairement, on réinjecte une décomposition en série entière $ ϕ(x,p)=ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $
On résout l'équation obtenu par puissance de p croissantes avec les nouvelles conditions initiales.

Ordre 0

$ \phi_{0,xx}=0 $ soit $ \phi_0=A_0x+B_0 $.

Introduisant les conditions limites suivantes: $ \phi_{0,x}^L=0 $ et $ \phi_{0,x}^0=ik(2-\phi_{0}^0) $, il vient :

• $ \phi_{0,x}^L=0 → A_0 = 0 $
• $ \phi_{0,x}^0=ik(2-\phi_{0}^0) → A_0=ik(2-B_0) → B = 2 $

D’où : $ \color{NavyBlue}\phi_0=2 $.

Ordre 1

$ \phi_{1,xx}-\phi_{0,xx}+\phi_{0,xx}+k^2\phi_0=0 $ soit $ \phi_{1}=-k^2\int\phi_0dxdx +A_1x+B_1 $.

Toujours avec les conditions aux limites : $ ϕ_x^L=0 $ et $ ϕ_x^0=ik(2−ϕ^0) $
Il vient :

• $ ϕ_x^L=0 → ϕ_{1,x}^L=0 → A_1 = 2k^2L $
• $ ϕ_x^0=ik(2−ϕ^0) → ϕ_{1,x}^0=-ikϕ_1^0 → B_1 = 2ikL $

D’où : $ \color{NavyBlue}\phi_1= -k^2x^2 +2k^2Lx+2ikL $.

Ordres supérieurs

A chaque ordre supérieur : $ \phi_{i}=-k^2\int\phi_{i-1}dxdx +A_ix+B_i $. Similairement les conditions limites sont :

• $ ϕ_{i,x}^L=0 $
• $ ϕ_{i,x}^0=-ikϕ_i^0 $

Ensuite on additionne les $ \phi_{i} $ en pondérant par les puissances de $ p^i $.

On en déduit la hauteur $ h $ de la houle avec l'expression : $ \color{NavyBlue} h(x,t)=R(Φ\text{e}^{-iωt}) $

Pour p=1, K=1 et L=1/100 on obtient aux différents ordres :

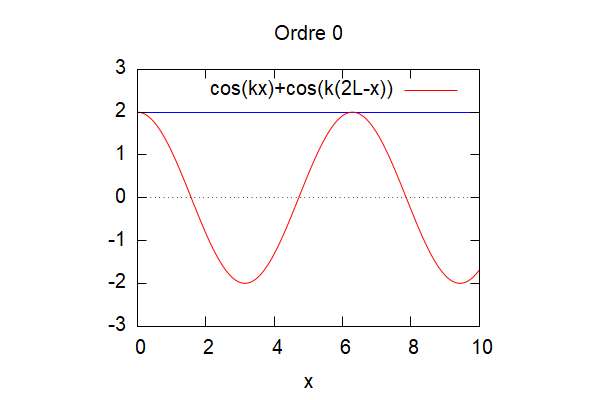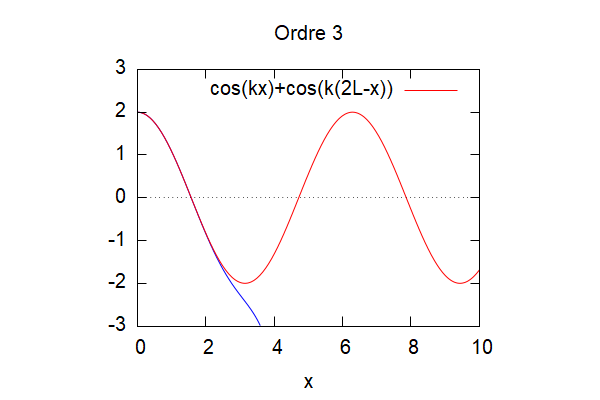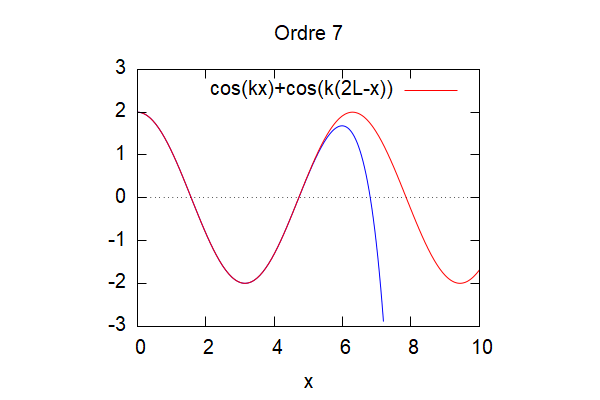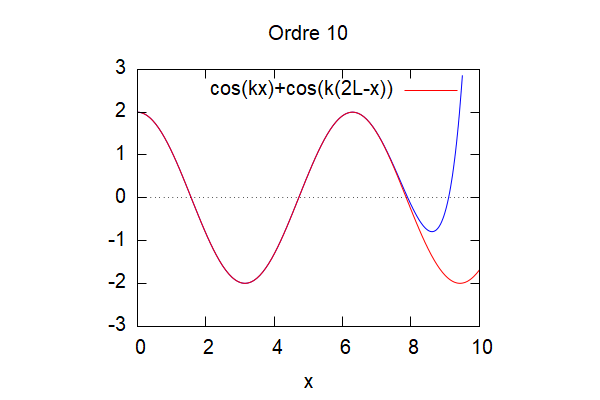
Le résultat ne converge pas forcément selon les valeurs de K et L choisi : pour k=1 et L=1 voila ce que l'on obtient :

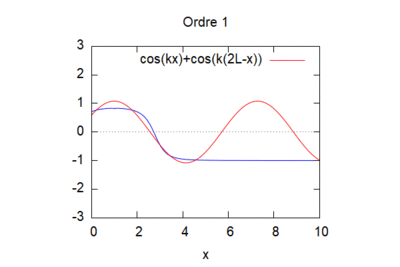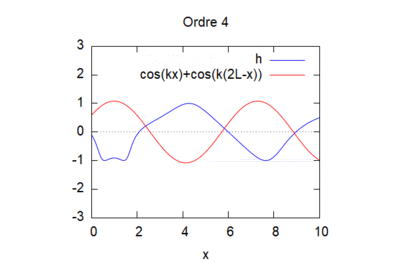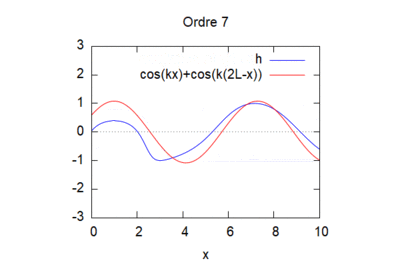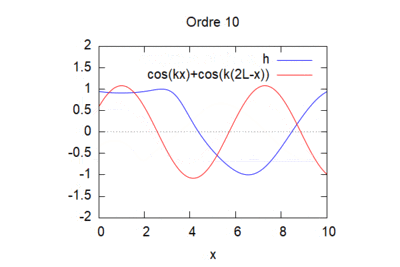
Cas n°3 : Canal monodimensionnel avec pente du fond constante, entrée par l'aval d'une onde de fréquence unitaire et sortie libre amont

On se place dans les conditions initiales du cas n°1 $ ϕ=1 $ et $ ϕ_x=ikϕ $
auxquelles on ajoute une pente du canal constante s=cste.

Le problème devient alors plus complexe : H(x) n'est plus égale à $ H_0 $ mais à $ H(x)= H_0 -sx $

En reprenant ainsi de modèle de Berkhoff : $ ∇.(CCg∇ϕ)+k^2CCgϕ=0 $ et en remplaçant $ CCg = gH(x) $ On obtient : $ H(x)\phi_{xx}-s\phi_{x}+k^2H(x)\phi=0 $

Solution analytique

On cherche à résoudre l'équation suivante : $ (H_0 -sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $

On cherche à mettre cette expression sous la forme de l'équation de Bessel, c'est à dire : $ z^2\phi_{zz}+z\phi_{z}+(\dfrac {k^2} {s^2})z^2 \phi=0 $

On pose donc : $ z=H_0−sx $

On obtiendra donc une solution de la forme : $ \phi(x)=A∗J_0(X)+B∗Y_0(X) $
avec J0 une fonction de Bessel de 1ère espèce et Y0 une fonction de Bessel de 2ème espèce.

On a les conditions limites :

$ \phi(0)=1 $
et $ \phi_x(L)=ik \phi(L) $

On obtient donc finalement : $ \color{NavyBlue} \phi(x) = \dfrac{J_0(x)(ikY_0(L)-iY_1(L))+Y_0(x)(J_1(L)-ikJ_0(L))} {J_0(0)(ikY_0(L)-Y_1(L))+Y_0(0)(J_1(L)-ikJ_0(L))} $

Solution par homotopie

On résout par homotopie : $ (1-p)\phi_{xx} + p((H_0 -sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi)=0 $
Similairement, on réinjecte une décomposition en série entière $ ϕ(x,p)=ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $
On résout l'équation obtenu par puissance de p croissantes avec les nouvelles conditions initiales.

Ordre 0

A l'ordre 0 on résout : $ \phi_{0,xx}=0 $ soit $ \phi_0=Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :

$ \color{NavyBlue}\phi_0=1+\dfrac{ik}{1-ikL}x $.

Ordre 1

A l'ordre 1, l'expression est : $ \phi_{1,xx}-\phi_{0,xx}+(H_0-sx)\phi_{0,xx}-s\phi_{0,x}+k^2(H_0-sx)\phi_0=0 $
Cette expression se simplifie $ \phi_{1,xx}-s\phi_{0,x}+k^2(H_0-sx)\phi_0=0 $

Connaissant $ \phi_0 $ on intègre deux fois l'expression précédente pour obtenir $ \phi_1 $ avec les conditions aux limites $ \phi_1^0=0 $ et $ \phi_{1,x}^L=ik\phi_{1}^L $

Ordre 2

A l'ordre 2 en p on a : $ \phi_{2,xx}-\phi_{1,xx}+(H_0-sx)\phi_{1,xx}-s\phi_{1,x}+k^2(H_0-sx)\phi_1=0 $.
Similairement, on a les conditions initiales suivantes $ \phi_2^0=0 $ et $ \phi_{2,x}^L=ik\phi_{2}^L $.

Ordre n

A l'ordre $ n>1 $, on a : $ \phi_{n,xx}-\phi_{n-1,xx}+(H_0-sx)\phi_{n-1,xx}-s\phi_{n-1,x}+k^2(H_0-sx)\phi_{n-1}=0 $.
On résout cette équation par récurrence avec les conditions initiales suivantes $ \phi_2^0=0 $ et $ \phi_{2,x}^L=ik\phi_{2}^L $.

Cas n°4 : Canal monodimensionnel avec pente du fond exponentielle, entrée par l'aval d'une onde de fréquence unitaire et sortie libre amont

On se place dans les conditions initiales du cas n°1 $ ϕ=1 $ et $ ϕ_x=ikϕ $
auxquelles on ajoute une pente du canal exponentielle s. On a alors $ H(x)=H_0e^{-sx} $

En reprenant ainsi de modèle de Berkhoff : $ ∇.(CCg∇ϕ)+k^2CCgϕ=0 $ et en remplaçant $ CCg = gH(x) $
On obtient : $ H(x)\phi_{xx}-H'(x)\phi_{x}+k^2H(x)\phi=0 $
ie $ H_0e^{-sx}\phi_{xx}-sH_0e^{-sx}\phi_{x}+k^2H_0e^{-sx}\phi=0 $
ie $ \phi_{xx}-s\phi_{x}+k^2\phi=0 $

Solution analytique

Dans ce cas, la hauteur est de la forme : $ H(x)=H_0\mathrm{e}^{-sx} $

L'équation de Berkhoff associée est donc $ H(x)\phi_{xx}-sH(x)\phi_{x}+k^2H(x)\phi=0 $ Soit, par factorisation : $ H(x)(\phi_{xx}-s\phi_{x}+k^2\phi)=0 $

Or H(X) est non nul donc on résout $ \phi_{xx}-s\phi_{x}+k^2\phi=0 $

L'équation caractéristique associée est : $ x^2-sx+k^2=0 $
Cette équation à pour discriminant : $ \Delta=s^2-4k^2 $ pouvant être positif, négatif ou nul.

1. Si $ \Delta>0 $, la solution sera de la forme : $ \phi(x) = A \text{e}^{r_1x} + B \text{e}^{r_2x} $.

2. Si $ \Delta<0 $, la solution sera de la forme : $ \phi(x)=\mathrm{e}^{\frac{s}{2}x}[A\cos\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)+B\sin\Big(\frac{\sqrt{s^2-4k^2}}{2}x\Bigr)] $

3. Si $ \Delta=0 $, la solution sera de la forme : $ \phi(x)=(Ax+B)\mathrm{e}^{\frac{s}{2}x} $

On cherche $ A $ et $ B $ grâce aux conditions initiales : $ \phi(0)=1 $ et $ \frac{\partial\phi}{\partial_x}(L)=ik\phi(L) $

cas 1 : $ \Delta>0 $

On obtient : $ r_1 = \frac{ s - \sqrt{s^2 - 4k^2}}{2} $ et $ r_2 = \frac{ s + \sqrt{s^2 - 4k^2}}{2} $

Les conditions initiales permettent d'avoir : $ A=1-\frac{ik\mathrm{e}^{r_1L}-r_1\mathrm{e}^{r_1L}}{r_2\mathrm{e}^{r_2L}-r_1\mathrm{e}^{r_1L}+ik\mathrm{e}^{r_1L}-ik\mathrm{e}^{r_2L}} $ et $ B=\frac{ik\mathrm{e}^{r_1L}-r_1\mathrm{e}^{r_1L}}{r_2\mathrm{e}^{r_2L}-r_1\mathrm{e}^{r_1L}+ik\mathrm{e}^{r_1L}-ik\mathrm{e}^{r_2L}} $

La solution est donc : $ \color{NavyBlue}\phi(x) = (1-\frac{ik\mathrm{e}^{r_1L}-r_1\mathrm{e}^{r_1L}}{r_2\mathrm{e}^{r_2L}-r_1\mathrm{e}^{r_1L}+ik\mathrm{e}^{r_1L}-ik\mathrm{e}^{r_2L}})\text{e}^{r_1x} + \frac{ik\mathrm{e}^{r_1L}-r_1\mathrm{e}^{r_1L}}{r_2\mathrm{e}^{r_2L}-r_1\mathrm{e}^{r_1L}+ik\mathrm{e}^{r_1L}-ik\mathrm{e}^{r_2L}} \text{e}^{r_2x} $

cas 2 : $ \Delta<0 $

Pour simplifier les calculs, on pose : $ \gamma=\frac{\sqrt{s^2-4k^2}}{2} $

Les conditions initiales permettent d'obtenir : $ A=1 $ et $ B=\frac{\gamma\sin(\gamma L)+\cos(\gamma L)(ik-1)}{\gamma\cos(\gamma L)+\sin(\gamma L)(1-ik)} $

La solution est donc : $ \color{NavyBlue}\phi(x)=\mathrm{e}^{\frac{s}{2}x}[\cos(\gamma x)+\frac{\gamma\sin(\gamma L)+\cos(\gamma L)(ik-1)}{\gamma\cos(\gamma L)+\sin(\gamma L)(1-ik)}\sin(\gamma x)] $

cas 3 : $ \Delta=0 $

Grâce aux conditions initiales, on a: $ A=\frac{ik - \frac{s}{2}}{1 + \frac{s}{2}L - ikL} $ et $ B=1 $

La solution est donc : $ \color{NavyBlue}\phi(x) = (\frac{\frac{s}{2} - ik}{ikL - 1 - \frac{s}{2}L}x+1)\text{e}^{\frac{s}{2}x} $

Solution par homotopie

On résout par homotopie : $ (1-p)\phi_{xx} + p(\phi_{xx}-s\phi_{x}+k^2\phi)=0 $
Similairement, on réinjecte une décomposition en série entière $ ϕ(x,p)=ϕ_0(x)+pϕ_1(x)+p^2ϕ_2(x)+p^3ϕ_3(x)+... $
On résout l'équation obtenue par puissance de p croissantes avec les nouvelles conditions initiales.

Ordre 0

A l'ordre 0 on résout : $ \phi_{xx,0} $ soit $ \phi_0=Ax+B $.

Introduisant les conditions limites suivantes: $ \phi_0^0=1 $ et $ \phi_{0,x}^L=ik\phi_{0}^L $, il vient :

$ \color{NavyBlue}\phi_0=1+\dfrac{ik}{1-ikL}x $.

Ordre 1

A l'ordre 1 on résout : $ \phi_{xx,1}-s\phi_{x,0}+k^2\phi_{0}=0 $

Ordre 2

A l'ordre 1 on résout : $ \phi_{xx,2}-s\phi_{x,1}+k^2\phi_{1}=0 $

Ordre n

A l'ordre n on résout : $ \phi_{xx,n}-s\phi_{x,n-1}+k^2\phi_{n-1}=0 $

Analyse des résultats, limites et intérêt de la méthode d'homotopie

Intérêts de la méthode d'homotopie

La méthode d'homotopie permet de partir d’une solution connue relativement simple et de converger vers une solution complète. L’introduction d'un paramètre p qui varie entre 0 et 1 permet d’assurer une déformation continue entre une première estimation de la solution relativement simple (p=0) et la valeur finale de la solution (p=1) du système d’équations à résoudre. Cette méthode permet donc d’atteindre la solution finale avec peu de terme et en utilisant la résolution formelle facilement programmable à l’aide d’outils de calcul formel tels que WSMAXIMA.

Limites des résultats obtenus

Notre modèle ne prend pas en compte un certain nombre de paramètres naturels tels que les fonds océaniques irréguliers, avec des sédiments par forcément répartis de manière uniforme, l'irrégularité des traits de côte qui entraînent des phénomènes de diffraction/réfraction. De plus, l'énergie cinétique des vagues n'est pas prise en compte alors que c'est un paramètre majeur pour considérer l'érosion du trait de côte et les submersions marines. De plus on considère certaines variables constantes (Letc,k,ω) alors que ce n'est pas forcément le cas dans la réalité. Ces approximations nous permettent de trouver les solutions mais elles nuisent au réalisme du modèle.