Utilisateur:Jean-Michel Tanguy/SujetENTPE2021/BILLARD - PAYET - VILAYVONG
Fiche: Impact du changement climatique sur les côtes
Réalisée par Léo Billard, Alec Villayvong, et Arnaud Payet
Contexte
Le changement climatique est responsable de beaucoup de problèmes: réchauffement des températures, acidification des océans, augmentation du niveau de la mer et donc une obligation de migration de certaines populations pour échapper à ces montées du niveau des océans. Dans ce projet, on tachera de modéliser l'impact du changement climatique sur le littoral.
Il conviendra de quantifier et de modéliser les conséquences de ce changement climatique sur la propagation des houles. Différents cas seront étudiés. Nous utiliserons le modèle de Berkhoff afin des modéliser les houles. Il s'agit d'une équation aux dérivées partielles comme on le verra dans la section suivante. Une méthode analytique et une méthode d'homotopie permettrons de résoudre cette équation de Berkhoff. Enfin, une étude de sensibilité en fonction du nombre d'onde k sera faite à chaque cas étudiés.
Côte érodée au Nord de Madagascar.
Cas n°1: canal uniforme unidimensionnel avec sortie libre en amont.
Les conditions aux limites sont les suivantes : entrée à l'aval $ Ф(x=0)=1 $ et en sortie libre à l'amont $ \frac{\partial Ф(x=L)}{\partial x}= ik Ф(x=L) $.
Résolution analytique.
Le modèle de Berkhoff est le suivant : $ \nabla(CC_{g}\nabla(Ф))+k^{2}CC_{g}Ф = 0 $. Or On fait les hypothèses $ C=C_{g} $, donc le modèle de Berkhoff devient $ C^{2}\Delta(Ф)+k^{2}C^{2}Ф=0 $, et donc $ \frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф=0 $. L'équation caractéristique associée est de la forme $ ar^{2}+br+c=0 $. On trouve alors $ \Delta=-4k^{2} $, et donc $ Ф(x)=Ae^{-ikx}+Be^{ikx} $ et donc $ \frac{\partial^{1}Ф(x)}{\partial x}=-ikAe^{-ikx}+ikBe^{ikx} $ où (A,B) $ \in $ $ R^{2} $.
On détermine A et B grâce aux conditions aux limites.
$ Ф(x=0)=1=A+B $
$ Ф_x(x=L)=-ikAe^{-ikL}+ikBe^{ikL}=ik(Ae^{-iKL}+Be^{ikL}) $.
De la deuxième condition aux limites on trouve $ A=0 $ et donc avec la première $ B=1 $.
Ainsi, $ \color{Red}Ф(x)=e^{ikx} $ et en restituant la partie temporelle, $ Ф(x,t)=e^{i(kx-ωt)} $.
Enfin la hauteur se traduit par : $ \color{Red}h(x,t)=Re(Ф(x,t))=cos(kx-ωt) $
Résolution par homotopie.
Le principe de la méthode d'homotopie permet de "passer", grâce à un paramètre p variant dans [0,1], d'une solution connue assez simple à une autre solution qui est complète. Le paramètre p vaut 0 pour une première estimation simple de a solution, et on donne ensuite la valeur 1 à p pour la valeur finale de la solution. L'avantage de cette méthode est qu'elle converge rapidement, c'est-à-dire qu'elle permet d'obtenir une solution finale rapidement.
La relation d'homotopie s'écrit en choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle:
$ (1−p)\frac{\partial^{2} Ф}{\partial x^2}+p(\frac{\partial^{2} Ф}{\partial x^2}+k^{2}Ф)=0 $
Ordre 0.
$ \frac{\partial^{2} Ф_{0}}{\partial x^2}=0 $, donc $ Ф_{0}=Ax+B. $
En utilisant les conditions limites, on trouve:
$ B=1 $ et $ A=\frac{ik}{1-ikL} $.
Donc, $ \color{Red}Ф_{0}(x)=\frac{ik}{1-ikL}x+1 $.
Ordre 1.
$ Ф_{1,xx}-Ф_{0,xx}+Ф_{0,xx}-k^{2}Ф_{0}=0 $ donc on a $ Ф_{1}=-k^{2}\iint(Ф_{0})+Ax+B $.
Avec les conditions limites, $ Ф_{1}(x=0)=0 $ et $ Ф_{1,x}(x=L)=ikLФ_{1}(x=L) $ on a $ \color{Red}Ф_{1}(x)=-\frac{k^{2}L(k^{2}L^{2}+3ikL-3)}{3(1-ikL)^{2}}x-k^{2}(\frac{ik}{6(1-ikL)}x^{3}+\frac{1}{2}x^{2}) $
On continue jusqu'à l'ordre n avec un logiciel de calcul afin de trouver toutes les itérations de Ф et ensuite on peut déterminer: $ h(x,t)=Re((Ф_{0}+Ф_{1}+...+Ф{n})e^{-iwt}) $.
On prend $ k=\frac{1}{100} $ et $ k=\frac{1}{L} $.
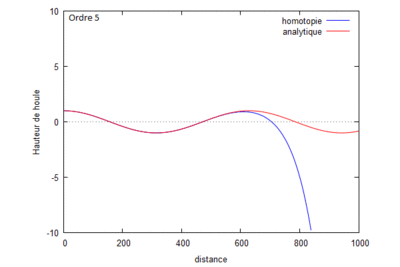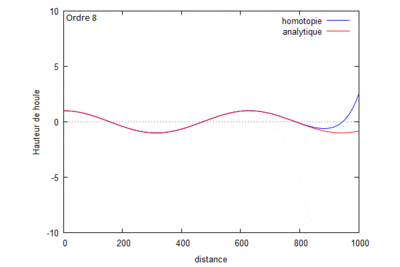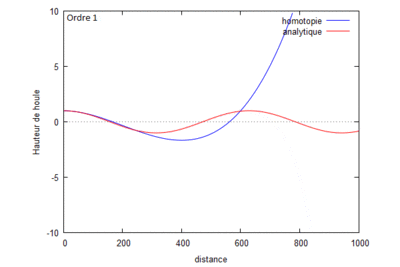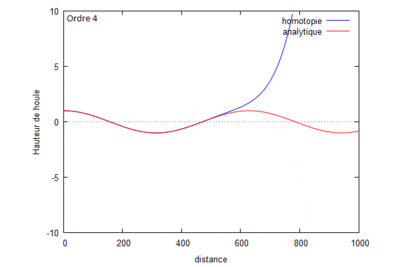
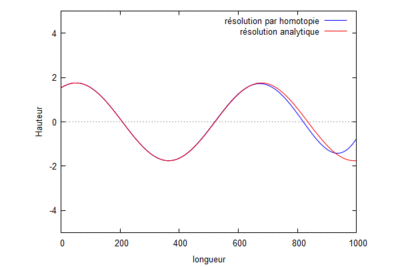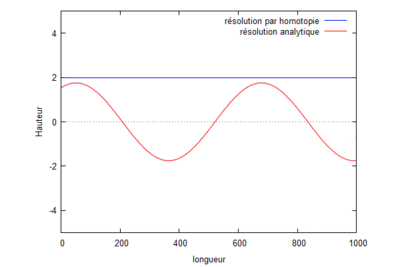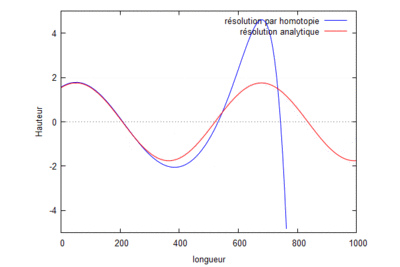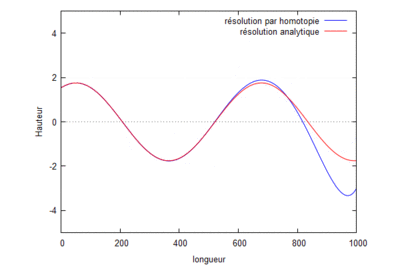
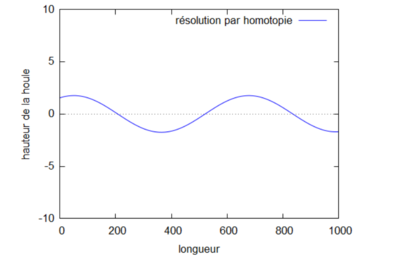
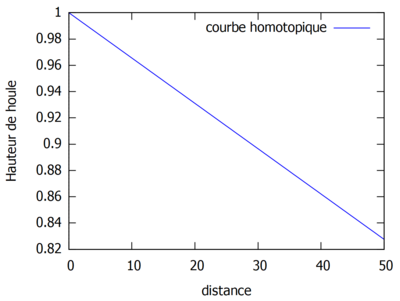
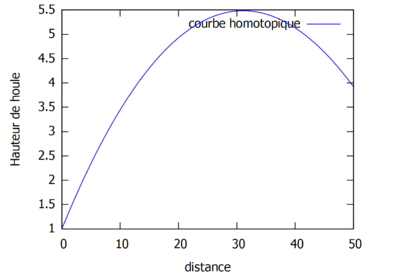
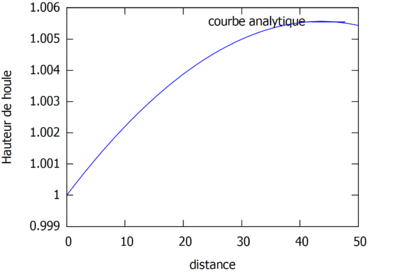
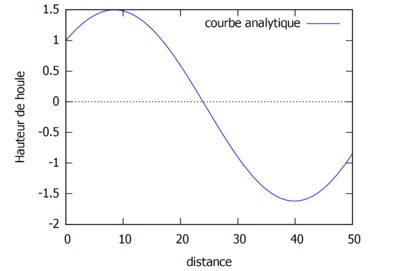
Superposition des résolutions analytiques et homotopiques (où kL=1) pour différents ordres.
On s'aperçoit que la solution homotopique converge bien vers la solution analytique.
Etude de sensibilité des paramètres
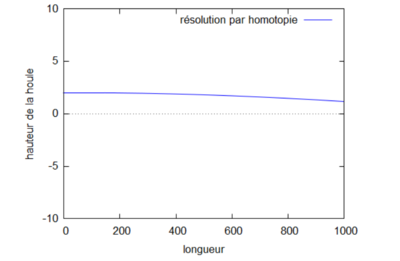
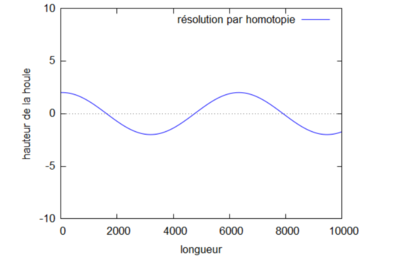
On étudie le changement sur la houle qu'implique le changement de la valeur de k. Pour cela, on fixe $ L=4 $ et on prend dans un premier cas $ k=\frac{1}{16} $ de sorte à ce que $ kL<1 $ (gif de gauche), et dans un second cas $ k=\frac{1}{3} $ de sorte à ce que $ kL>1 $ (gif de droite).
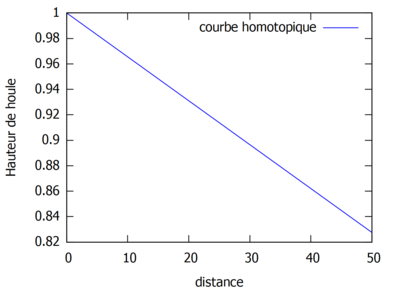
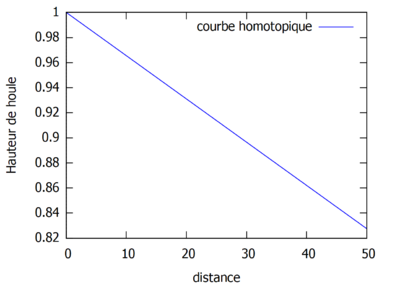
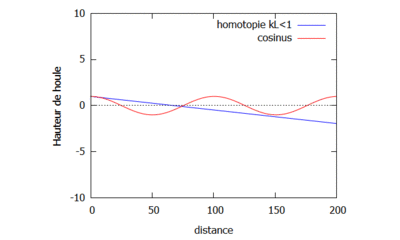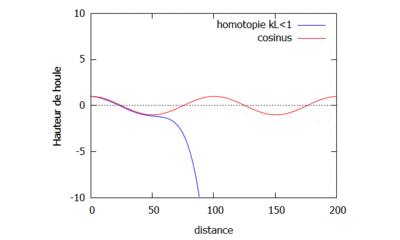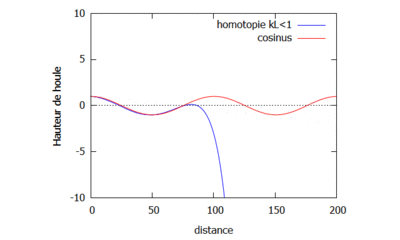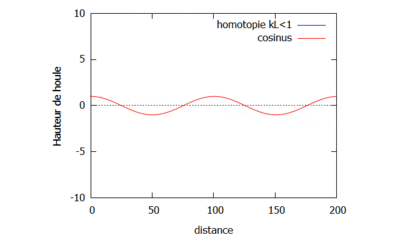 Courbes homotopiques où kL<1.
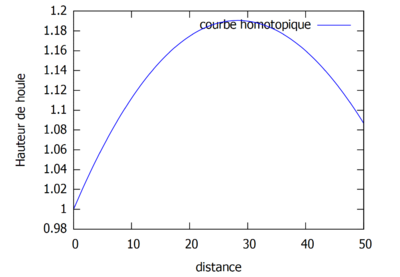
Courbes homotopiques où kL<1. 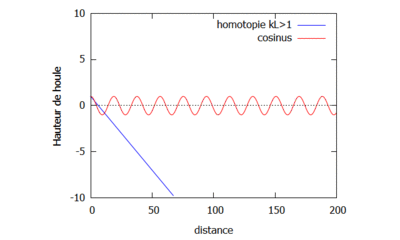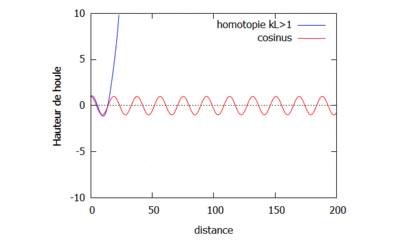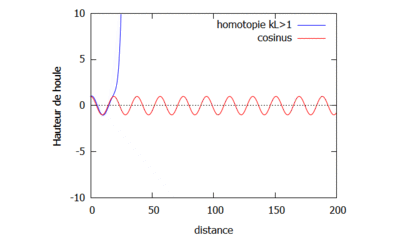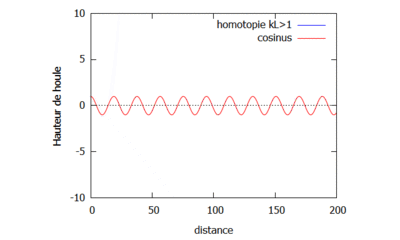 Courbes homotopiques où kL>1.
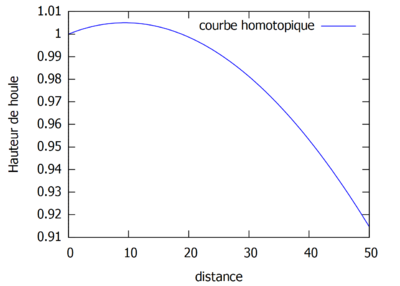
Courbes homotopiques où kL>1.
On observe que dans le cas où $ kL>1 $, les vagues semblent être plus proches les unes des autres que dans les cas où $ kL<1 $ et $ kL=1 $. Enfin il semblerait que quand k est petit, la courbe de la fonction homotopique converge plus rapidement vers la courbe de la fonction analytique.
Cas n°2: canal uniforme unidimensionnel avec réflexion totale en amont.
Les conditions aux limites sont les suivantes : à l'amont $ \frac{\partial^{1} Ф(x=L)}{\partial x}=0 $ et condition de flux à l'aval $ \frac{\partial^{1} Ф(x=0)}{\partial x}=ik(2-Ф(x=0)) $.
Résolution analytique.
Le modèle de Berkhoff est identique au cas n°1.
On détermine A et B grâce aux conditions aux limites: $ B=1 $ et $ A=e^{2ikL} $
Ainsi, $ \color{Red}Ф(x)=e^{ik(2L-x)}+e^{ikx} $ et en restituant la partie temporelle, $ Ф(x,t)=e^{i(-wt+k(2L-x))}+e^{i(kw-wt)} $.
Enfin la hauteur se traduit par: $ \color{Red}h(x,t)=Re(Ф(x,t))=cos(k(2L-x)-wt)+cos(kx-ωt) $.
Résolution par homotopie.
La méthode reste identique à celle du cas 1, seules les conditions limites changent.
Ordre 0:
Une fois les calculs fait avec les conditions limites, on a: $ \color{Red}Ф(x)=Ф_{0}(x)=2 $.
Ordre 1:
Une fois les calculs fait avec les conditions limites, on a: $ Ф_{1}(x)=-k^{2}x^{2}+2Lk^{2}x+2kLi $.
Et donc $ \color{Red}Ф(x)=2-k^{2}x^{2}+2Lk^{2}x+2kLi $.
On prend $ k=\frac{1}{100} $ et $ L=50 $.
Superposition des résolutions analytiques et homotopiques pour différents ordres.
La méthode homotopique converge bien vers la méthode analytique, au bout de l'ordre 15.
Etude de sensibilité des paramètres
Nous obtenons donc les mêmes résultats que dans le cas précédent puisque le fond est toujours plat. Cependant, l'amplitude de la vague est encore plus grande lorsque la profondeur est grande à cause du phénomène de réflexion.
Cas n°3: canal uniforme unidimensionnel avec pente constante et sortie libre en amont.
Les conditions limites sont les suivantes: en aval Ф=1, et en amont une sortie libre $ Ф_{x}=ikФ $
L’équation de Berkhoff est identique a celles utilisées dans les cas 1 et 2. On prend $ H(x)=-sx+H_{0} $ où s représente la pente et $ H_{0} $ la hauteur initiale. On a donc: $ H(x)Ф_{xx}+H’(x)Ф_{x}(x)+k^{2}(x)H(x)Ф(x)=0 $.
Cas où k est constant.
Résolution analytique.
On fait les changements de variable suivants: $ z= H_{0}-sx $, et $ b^{2}=\frac{k^{2}}{s^{2}} $. L’équation de Bessel devient donc $ z^{2}Ф_{zz}+zФ_{z}+b^{2}z^{2}Ф=0 $.
La solution est sous forme $ \color{Red}Ф(z)=AJ_{0}(bz)+BY_{0}(bz) $, où A et B sont à déterminer avec les conditions limites. On note $ z_{0}=bH_{0}=\frac{k_{0}} {s} H_{0} $ et $ z_{L}=b(H_{0}-sL)=\frac{k_{0}} {s}(H_{0}-sL) $. Ainsi, A et B ont pour expression:
$ A=\frac{iY_{0}(z_{L})-Y_{1}(z_{L})}{(iY_{0}(z_{L})-Y_{1}(z_{L}))J_{0}(z_{0})+Y_{0}(z_{0})(J_{1}(z_{L})-iJ_{0}(z_{L}))} $ et $ B=\frac{1}{Y_{0}(z_{0})+J_{0}(z_{0})\frac{iY_{0}(z_{L})-Y_{1}(z_{L})}{J_{1}(z_{L})-iJ_{0}(z_{L})}} $.
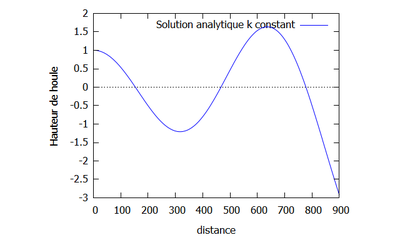
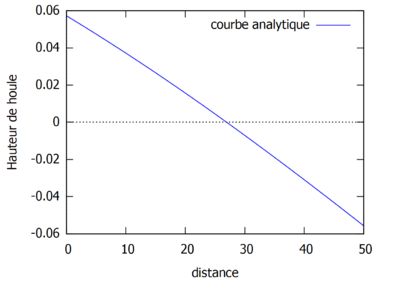
Voici la courbe de la solution analytique, avec $ s=\frac{1}{200} $ et $ L=40 $ (longueur du domaine d'une houle en général) et $ k=0.01 $ et $ H_{0}=5 $ (hauteur initiale, prise arbitrairement).
Résolution par homotopie.
On a $ (-sx+H_{0})Ф_{xx}(x)-sФ_{x}(x)+k^{2}(-sx+H_{0})Ф(x)=0 $, donc la relation d’homotopie est la suivante, $ (1-p)Ф_{xx}+p((H_{0}-sx)Ф_{xx}-sФ_{x}+k^{2}(H_{0}-sx)Ф_(x)=0 $.
Ordre 0:
Une fois les calculs fait avec les conditions limites, on a: $ Ф_{0}(x)=\frac{ik}{1-ikL}x+1 $
Ordre 1:
On a d'après la relation d'homotopie, $ Ф_{1,xx}-Ф_{0,xx}+(H_{0}-sx)Ф_{0,xx}-sФ_{0,x}+k^{2}(H_{0}-sx)Ф_{0}=0 $.
Ainsi, $ Ф_{1,xx}=sФ_{0,x}-k^{2}(H_{0}-sx)Ф_{0} $.
Après calculs on trouve, $ \color{Red}Ф_{1}(x)=\frac{iskx^{2}}{2(1-ikL)}-k^{2}H_{0}(\frac{ikx^{3}}{6(1-ikL)}+\frac{x^{2}}{2})+k^{2}s(\frac{x^{3}}{6}+\frac{ikx^{4}}{12(1-ikL)})+Ax+B $ où A et B sont à déterminer avec les conditions limites, et qui valent: $ B=0 $ et $ A= \frac{kL}{12(1-ikL)^{2}} (2k^{3}H_{0}L^{2}-k^{3}L^{3}s-12is+6ik^{2}H_{0}L-4ik^{2}L^{2}s-6ksL ) + \frac{k^{2}L}{6(1-ikL)}(ikL^{2}s-3ikLH_{0}+6H_{0}-3sL) $.
Voici les courbes pour les ordre 0 (à gauche) et 1 (à droite), où on a pris $ s=\frac{1}{200} $ et $ L=40 $ (longueur du domaine d'une houle en général) et $ k=0.01 $ et $ H_{0}=5 $ (hauteur initiale, prise arbitrairement).
Cas où k n'est pas constant.
Résolution analytique.
On a cette fois $ k^{2}= \frac{k_{0}^{2}*H_{0}}{H(x)} $, avec toujours $ H(x)=H_{0}-sx $.
On pose cette fois $ b^{2}=\frac{k_{0}^{2}H_{0}}{s} $, $ z_{0}=\frac{k_{0}H_{0}\sqrt{H_{0}}}{s} $ et $ z_{L}=\frac{k_{0}(H_{0}-sL)\sqrt{H_{0}}}{s} $.
L'équation de Berkhoff devient, $ zФ_{zz}+Ф_{z}+b^{2}Ф=0 $, et on a toujours $ Ф(z)=AJ_{0}(bz)+BY_{0}(bz) $ où A et B sont identiques au cas où k est constant.
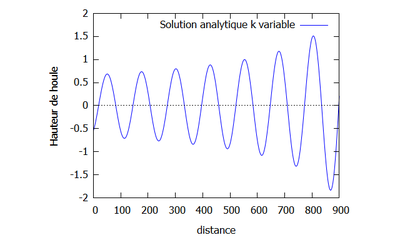
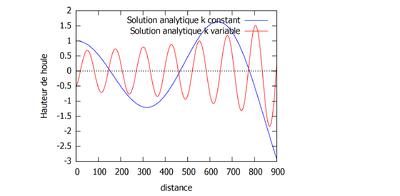
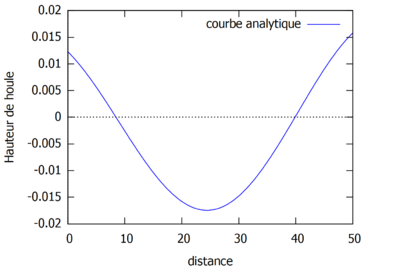
La courbe de la résolution analytique est tracée ci-dessous (à gauche), avec les mêmes valeurs prises pour s, L, k et $ H_{0} $ que pour le cas où k est constant. La superposition des courbes avec k constant et k non constant est tracée ci-dessous (à gauche).
On observe que dans les cas où k sont constant et non constant l'amplitude finale semble être identique. Néanmoins, on voit que dans le cas ou k est variable, la houle est plus mouvementée que quand k est constant.
Résolution par homotopie.
On pose $ ξ=\frac{s}{H_{0}} $.
Ordre 0:
Une fois les calculs faits avec les conditions limites, on a $ Φ_{0}(x)=\frac{ik_{L}}{1-ik_{L}L}x+1 $
Ordre 1:
La relation est $ Φ_{1,xx}-Φ_{0,xx}+(1-ξx)Φ_{0,xx}-ξΦ_{0,x}+k_{0}^{2}Φ_{0}=0 $.
Ainsi, on trouve $ \color{Red}Φ_{1}(x)= \frac{iξk_{L}x^{2}}{2(1-ik_{L}L)} - \frac{k_{0}^{2}x^{2}}{2} - \frac{ik_{0}^{2}k_{L}x^{3}}{6(1-ik_{L}L)} +Ax+B $ où A et B sont déterminés avec les conditions limites, et valent $ B=0 $ et $ A= \frac{-k_{L}L}{6(1-ik_{L}L)^{2}} ( 3ξLk_{L} -k_{0}^{2}k_{L}L^{2} -3ik_{0}^{2}L +6iξ ) - \frac{ik_{0}^{2}Lk_{L}^{2}}{2(1-iLk_{L})} + \frac{k_{0}^{2}L}{1-iLk_{L}} $
Les courbes pour les ordre 0 (à gauche) et 1 (à droite) ont été tracées pour $ s=\frac{1}{200} $ et $ L=40 $, $ k_{L}=0.01 $ (pris arbitrairement), $ k_{0}=0.1 $ (pris arbitrairement) et $ H_{0}=5 $.
Les formes des 2 courbes sont identiques à celles du cas où k est constant. Néanmoins, il semblerait que dans l'ordre 1, l'amplitude soit 4 fois supérieure dans le cas où k n'est pas constant.
Cas n°4: Canal monodimensionnel de largeur uniforme, de longueur L avec forme du fond exponentielle et sortie libre amont, où k est constant
Les conditions limites sont les suivantes: en aval $ Ф(x=0)=1 $, et en amont une sortie libre $ Ф_{x}=ikФ $. Puis à partir de l'ordre 1, on a en aval $ Ф(x=0)=0 $ et toujours en amont une sortie libre $ Ф_{x}=ikФ $.
L’équation de Berkhoff est identique a celles utilisées dans les cas 1 et 2 et 3. On prend $ H(x)=H_{0}e^{-sx} $ où s représente la pente et $ H_{0} $ la hauteur initiale. On a donc: $ \color{Red}Ф_{xx}-sФ_{x}(x)+k^{2}Ф(x)=0 $
Résolution analytique.
Premier cas: $ Δ=s^{2}-4k^{2}>0 $.
On a $ r_{1}=\frac{s-\sqrt{s^{2}-4k^{2}}}{2} $ et $ r_{2}=\frac{s+\sqrt{s^{2}-4k^{2}}}{2} $.
Tout calculs faits, on trouve $ \color{Red}Ф(x)=\frac{(r_{2}-ik)e^{r_{2}L+r_{1}x}+(ik-r_{1})e^{r_{1}L+r_{2}x}}{(ik-r_{1})e^{r_{1}L}+(r_{2}-ik)e^{r_{2}L}} $. En voici la courbe analytique.
On a pris dans les deux cas, $ s=\frac{1}{200} $ et $ L=40 $ (longueur du domaine d'une houle en général), et dans la première image $ k=0.01 $ et dans la seconde $ k=0.1 $.
Second cas: $ Δ=s^{2}-4k^{2}=0 $.
On a $ k=\frac{s}{2}=r_{0} $.
Tout calculs faits, on trouve $ \color{Red}Ф(x)=(\frac{ik-k}{1+kL-ikL}x+1)e^{kx} $. En voici la courbe analytique.
On a pris $ s=\frac{1}{200} $ et $ L=40 $ (longueur du domaine d'une houle en général) et $ k=0.01 $.
Troisième cas: $ Δ=s^{2}-4k^{2}<0 $.
On a $ r_{1}=\frac{s-i\sqrt{-(s^{2}-4k^{2})}}{2} $ et $ r_{2}=\frac{s+i\sqrt{-(s^{2}-4k^{2})}}{2} $.
Par la suite, on pose $ α=\frac{s}{2} $ et $ γ=\frac{\sqrt{-(s^{2}-4k^{2}})}{2} $.
Tout calculs faits, on trouve $ \color{Red}Ф(x)=e^{αx}(cos(γx)+\frac{(ik-α)cos(γL)+γsin(γL)}{(-ik+α)sin(γL)+γcos(γL)}sin(γL)) $. En voici la courbe analytique.
On a pris $ s=\frac{1}{200} $ et $ L=40 $ (longueur du domaine d'une houle en général) et $ k=0.01 $.
Résolution par homotopie.
Ordre 0:
Avec les conditions limites, on trouve $ Ф_{0}(x)=\frac{ikx}{1-ikL}+1 $
Ordre 1:
La relation homotopique est $ Ф_{1,xx}-Ф_{0,xx}+Ф_{0,xx}-sФ_{0,x}+k^{2}Ф_{0}=0 $.
Finalement, on trouve $ \color{Red}Ф_{1}(x)=\frac{iskx^{2}} {2(1-ikL)} - \frac{k^{2}x^{2}} {2} - \frac{ik^{3}x^{3}} {6(1-ikL)} +Ax+B $ où A et B sont à déterminer avec les conditions limites, et valent $ B=0 $ et $ A=\frac{kL} {6(1-ikL)^{2}} (k^{3}L^{2}-3skL-6is+3ik^{2}L ) + k^{2}L(1-\frac{ikL}{2}) $.
Les courbes à l'ordre 0 (à gauche) et à l'ordre 1 (à droite) ont été tracées pour $ s=\frac{1}{200} $ et $ L=40 $ et $ k=0.01 $.
Limites du modèle.
Le modèle semble limité, que ce soit d'un point de physique, mais aussi mathématique.
Les modèles étudiés avec la méthode d'homotopie ne prennent pas forcément en compte tous les paramètres naturels, tels que des fonds océaniques irréguliers, des différentes périodes des différents trains de vagues de la houle.
De même, le phénomène de transport des sédiments, du sable et des graviers, dû à le houle, ne sont pas pas pris en compte dans le modèle alors qu'il s'agit de paramètres pouvant influer sur le fond du canal et donc sur la houle.
De plus, l'hypothèse faite de fond plat, ne permet, elle aussi, pas de modéliser parfaitement la réalité.
Ainsi, tout ces paramètres ne sont pas pris en compte dans le modèle, et donc les modèles sont des modèles approchés de la réalité sans toutefois modéliser complètement la réalité.
Enfin, d'un point de vu mathématiques, certaines variables considérées constantes, telles que k, L et ω par exemple, ne sont sûrement pas réellement constante dans un modèle réelle, mais ont ici été prises comme constantes afin de simplifier le modèle.
Domaine d'utilisation du modèle.
Le modèle peut permettre de prédire les phénomènes de submersion marine, à savoir une inondation temporaire et possiblement épisodique de zones côtières lors d'évènements météorologiques majeurs tels que des cyclones par exemple. Le modèle peut aussi prédire l'impact de l'érosion sur les côtes du littoral.
Dégâts et inondations dû à une submersion marine en Charente-Maritine après la tempête Xynthia. (Source Wikipédia)
Images de la côte de Soulac en 1967 (photo de gauche) et en 2014 (photo de droite) qui a été érodée par la houle avec le temps.
Enfin, la méthode d'homotopie permet une adaptation à de nombreuses géométries et donc à de nombreux cas, ce qui permet de modéliser des formes d'estuaires et de littoraux complexes, et ainsi de travailler sur l'aménagement de ces lieux, pour en réduire l'érosion dû aux vagues et à la houle.
 S'abonner à un flux RSS
S'abonner à un flux RSS