Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/Emeline/Jallet

Sommaire

1 Modèle de Berkhoff

Modèle de Berkhoff

La houle peut être modélisée par l'équation aux dérivées partielles (EDP) issue du modèle de Berkhoff suivante :

$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $

Avec : $ \phi $ : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence $ \omega $, C : la célérité de l’onde, Cg : la célérité de groupe des vagues.

Résolution

Pour résoudre cette équation, nous utiliserons une méthode analytique lorsque cela sera possible et une méthode par homotopie. Nous nous placerons dans différent cas pour résoudre cette équation.

Cas N°1

Pour ce premier cas, nous étudierons le cas d'un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $(condition de Dirichlet) et sortie libre amont $ \phi_{x}=ik\phi $ (condition de Robin).

Méthode analytique

Dans cette situation l'équation issue du modèle de Berkhoff s'écrit : $ \phi_{xx} + k^2\phi=0 $.

Soit $ \phi(x) = Ae^{ikx}+Be^{-ikx} $ , A et B sont des constantes à déterminer avec les conditions initiales.

En aval pour x=0, $ \phi=1 $ donc $ A + B = 1 $

En amont pour x = L, $ \phi_{x}(L)=ik\phi{L} $

Donc $ ikAe^{ikL} - ikBe^{-ikL} = ik(Ae^{ikL} + Be^{-ikL}) $.

Ainsi A = 1 et B = 0

La solution analytique de cette équation est donc $ \phi(x)=e^{ikx} $

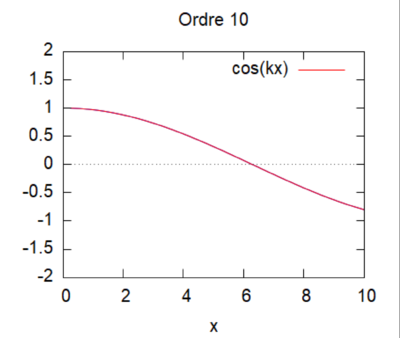
On s'intéresse à la partie réelle de $ \phi e^{i\omega t} $. Ainsi $ h(x,t) = cos(kx+ \omega t) $

Méthode par homotopie

En choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle, la relation d'homotopie devient :

$ (1-p)\phi_{xx}+ p(\phi_{xx}+k^2\phi)=0 $

Or $ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+... $

Et $ \phi_{xx}=\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+... $

Donc en injectant ces deux expressions dans la relation d'homotopie on a :

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $

Ordre 0 :

$ \phi_{xx}=0 $ donc $ \phi_{0,xx}(x)=0 $

En intégrant deux fois on a :

$ \phi_0(x)=Ax+B $

Avec pour conditions aux limites : $ \phi_0^0=1 $ et $ \phi_{0, x}^L={ik}\phi_0^L $ on a $ B=1 $ et $ A=\frac{ik}{(1-ikL)} $

Détail pour trouver A: $ \phi_{0, x}^L={ik}\phi_0^L $ $ \iff A=\frac{ik}{(AL+1)} $ $ \iff A=\frac{ik}{(1-ikL)} $

Ainsi $ \phi_0(x)=(\frac{ik}{(1-ikL)})x+1 $

Ordre 1 :

$ \phi_{1,xx}(x)={-k^2}\phi_0(x) $

donc par double intégration on a :

$ \phi_1(x) = -k^2\int\phi_0dxdx +Ax+B $.

Avec pour conditions aux limites :

$ \phi_1^0=0 $ et $ \phi_{1, x}^L={ik}\phi_1^L $

on a $ B=0 $ et $ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $

Calcul de A :

$ \phi_1(x)= -k^2(({ik}/({1-ikL})6)x^3+x^2/2+Ax $

en x=L:

$ \phi_{1, x}^L={ik}\phi_1^L $ $ \iff \frac{ikL^2}{(1-ikL)^2}+L+A=\frac{ik(ikL^3)}{(1-ikL)*6}+\frac{L^2}{2}+AL $

en isolant A dans l'équation on retrouve :

$ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $

On a donc :

$ \phi_{1}(x)= -\frac{k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2}x-k^2(\frac{ik}{6(1-ikL)})x^3+\frac{x^2}{2} $

Ordre 2 :

A partir des valeurs numériques suivantes :

$ k=\frac{1}{100} $ (nombre d'onde en m^-1)

$ H=40 $ (profondeur en m)

$ c=\sqrt{gH} $ (célérité de l'onde en m/s)

$ \lambda=\frac{2\pi}{k} $ (longueur d'onde en m)

$ L=2\lambda $ (longueur du domaine en m)

Etude de sensibilité

Cas kL=0,25

Cas kL=1

Cas kL=2

Cas N°2

Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_{x} =ik(2−\phi) $ et réflexion totale amont $ \phi_{x}=0 $.

Méthode analytique

Comme pour le cas N°1, l'équation de Berkhoff à une dimension s'écrit $ \phi_{xx} + k^2\phi = 0 $

Ce qui nous donne comme forme pour $ \phi $ : $ \phi(x) = Ae^{ikx} + Be^{-ikx} $

On peut déterminer les constantes A et B avec les conditions initiales de ce cas.

$ \phi_{x}(0) = ik(2 - \phi(0)) \iff ik(A - B) = ik(2 - A - B) $ $ \iff A = 1 $

Et $ \phi_{x}(L) = 0 \iff ik(Ae^{ikL} - Be^{-ikL}) = 0 \iff B = e^{2ikL} $

Ainsi $ \phi(x)= e^{ikx} + e^{2ikL}e^{-ikx} $

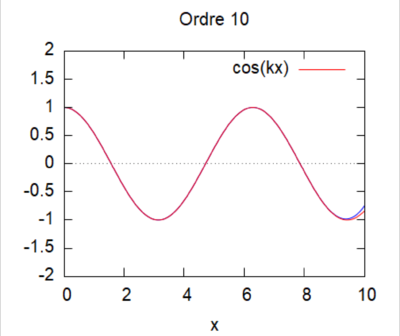
La solution réelle associée à cette fonction est $ h(x) = cos(kx) + cos(2kL+kx) $

Méthode par homotopie

En procédant de la même manière que dans le cas 1 on retrouve comme relation d'homotopie :

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $

Ordre 0 :

$ \phi_{0,xx}(x)=0 $

Par intégration on a :

$ \phi_0(x)=Ax+B $

Avec les conditions aux limites : $ \phi_{0,x}^0=ik(2-\phi) $ et $ \phi_{0, x}^L=0 $

On a :

$ A = 0 $ et $ B = 2 $

Donc $ \phi_0(x)=2 $

Ordre 1 :

On a $ \phi_{1,xx}(x) = -k^{2}\phi_0(x) $

donc $ \phi_1 (x) = -k^2x^2 + Ax + B $

Avec les conditions initiales on trouve pour A et B :

$ A = 2k^2L $ et $ B = 2ikL $

Donc $ \phi_1 (x) = - k^2x^2 + 2k^2Lx + 2ikL $

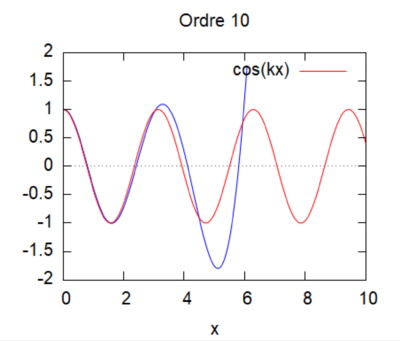
Etude de sensibilité

Cas N°3

Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec une pente de fond constante (s=cst). L'entrée se fait par l'aval avec une onde de fréquence unitaire $ \phi_{x} =ik(2−\phi) $ et la sortie en amont $ \phi_{x}(x=L)=ik\phi(x=L) $.

Le problème est complexifié puisque H(x) n'est plus égal à $ H_0 $ mais à $ H_0-sx $.

On a toujours $ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $ mais avec $ C=C_g=\sqrt{gH(x)} $

Soit $ {\displaystyle H(x)\frac{\partial^2 \phi}{\partial x^2} -\frac{\partial \phi}{\partial x} + k^2H(x) \phi = 0} $

Nous utilisons le changement de variable : $ z=H_0-sx $.

Et nous prenons: $ s = \frac{1/200} \ $.

Nous nous intéressons au cas $ k=ko\sqrt{Ho/H(x)} $.

Soit l'équation à résoudre : $ (H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $

On cherche une solution de la forme de l'équation de Bessel, c'est à dire de la forme : $ z^2\phi_{zz}+z\phi_{z}+(\dfrac{k^2}{s^2})z^2\phi=0 $

$ \phi(z)=AJ_0(\dfrac{k}{s}z)+BY_0(\dfrac{k}{s}z) $

Avec les conditions limites :

$ \phi(x=0)=1 $ et $ \phi_x(x=L)=ik \phi(x=L) $

Ce qui donne avec le changement de variable : $ \phi(z=H_0)=1 $ et $ \phi_z(z=H_0-sL)=ik \phi(z=H_0-sL) $

On obtient au final :

$ {\phi(z)=\frac{iY_0^L - Y_1^L}{J_0^0(iY_0^L - Y_1^L) + Y_0^0 (J_1^L-i J_0^L)} J_0 (2 \alpha \sqrt{z}) + \frac{J_1^L - i J_0^L}{J_0^0 (i Y_0^L-Y_1^L) + Y_0^0 (J_1^L - i J_0^L)} Y_0 (2 \alpha \sqrt{z})} $

Résolution par homotopie

Soit la relation d'homotopie suivante : $ (1-p)\phi_{xx}+p(H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $

ordre 0

$ \phi_{xx}=0 $ donc on a $ \phi_0=Ax+B $

et avec les conditions initiales on trouve : $ \phi_0=\frac{ik}{1-ikL}x+1 $

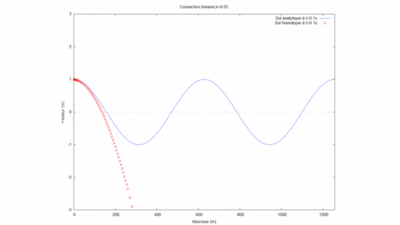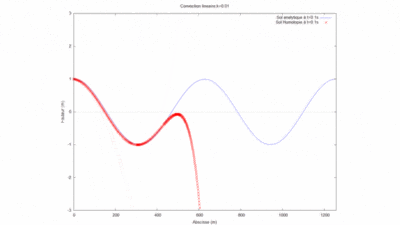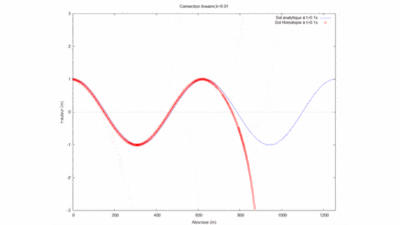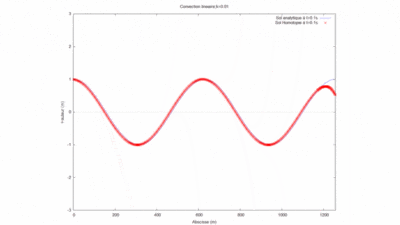
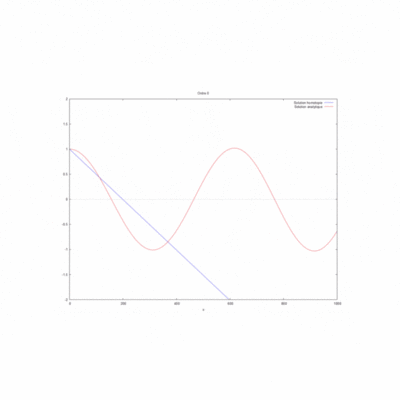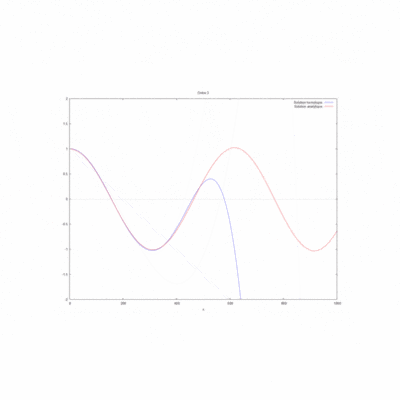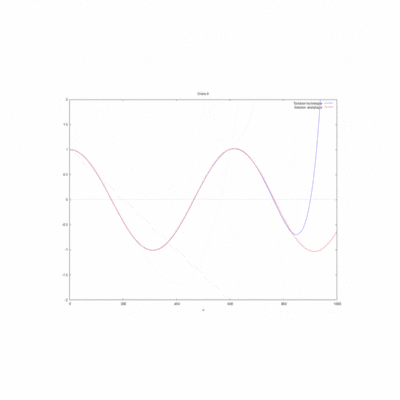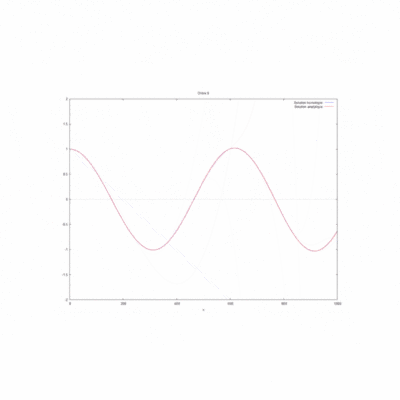
La simulation sur WXMaxima nous donne pour le produit kL=1 le gif suivant :

Cas N°4

Dans ce cas nous avons une vague sphérique générée par une source sinusoïdale

$ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $ Et en coordonnées polaires : $ \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $ avec $ r_0=1m $, $ R=100m $ et $ k=0.1m^{-1} $.