Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/Emeline/Jallet

Contexte

Le changement climatique et la monté des eaux est un enjeux actuel majeur pour les politiques publiques. Leurs impacts ne cessent d’augmenter et de menacer des terres et populations. Nous nous intéressons ici au phénomène de l'érosion du littoral. Les scientifiques sont formels : le littoral français s’érode de plus en plus. Aujourd’hui, on estime qu’environ 27% des côtes françaises métropolitaines sont en érosion (et ces zones deviennent de plus en plus vulnérables avec le temps…). La population qui vit près des côtes est, bien sûr, la première touchée. Jusqu'à 50 000 foyers français seront menacés par l'érosion du littoral d'ici la fin du siècle. Afin de prévenir et représenter ce phénomène d'actualité nous allons modéliser la houle à l'aide de la modélisation de Berkhoff. La résolution se réalisera de deux manières : analytiquement et par la méthode d'homotopie qui nécessite l'utilisation de logiciels d'approximation de polynômes tel que Maxima.

Lien pour la vidéo sur youtube : https://youtu.be/KtBmnqyWk2U

Modèle de Berkhoff

La houle peut être modélisée par l'équation aux dérivées partielles (EDP) issue du modèle de Berkhoff suivante :

$ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $

Avec :

$ \phi $ : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence $ \omega $, C : la célérité de l’onde, Cg : la célérité de groupe des vagues.

Résolution

Pour résoudre cette équation, nous utiliserons une méthode analytique lorsque cela sera possible et une méthode par homotopie.

Nous nous placerons dans différent cas pour résoudre cette équation.

Cas N°1

Pour ce premier cas, nous étudierons le cas d'un canal monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire $ \phi=1 $(condition de Dirichlet) et sortie libre amont $ \phi_{x}=ik\phi $ (condition de Robin).

Méthode analytique

Dans cette situation l'équation issue du modèle de Berkhoff s'écrit : $ \phi_{xx} + k^2\phi=0 $.

Soit $ \phi(x) = Ae^{ikx}+Be^{-ikx} $ , A et B sont des constantes à déterminer avec les conditions initiales.

En aval pour x=0, $ \phi=1 $

donc $ A + B = 1 $

En amont pour x = L, $ \phi_{x}(L)=ik\phi{L} $

Donc $ ikAe^{ikL} - ikBe^{-ikL} = ik(Ae^{ikL} + Be^{-ikL}) $.

Ainsi A = 1 et B = 0

La solution analytique de cette équation est donc $ \phi(x)=e^{ikx} $

On s'intéresse à la partie réelle de $ \phi e^{i\omega t} $. Ainsi $ h(x,t) = cos(kx+ \omega t) $

Méthode par homotopie

En choisissant la dérivée seconde comme fonction auxiliaire linéaire et en partant d'une solution initiale nulle, la relation d'homotopie devient :

$ (1-p)\phi_{xx}+ p(\phi_{xx}+k^2\phi)=0 $

Or

$ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+... $

Et

$ \phi_{xx}=\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+... $

Donc en injectant ces deux expressions dans la relation d'homotopie on a :

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $

Ordre 0

A l'ordre 0, on a:

$ \phi_{xx}=0 $

donc

$ \phi_{0,xx}(x)=0 $

En intégrant deux fois on a :

$ \phi_0(x)=Ax+B $

Avec pour conditions aux limites :

$ \phi_0^0=1 $ et

$ \phi_{0, x}^L={ik}\phi_0^L $

on a $ B=1 $ et $ A=\frac{ik}{(1-ikL)} $

Détail pour trouver A:

$ \phi_{0, x}^L={ik}\phi_0^L $

$ \iff A=\frac{ik}{(AL+1)} $

$ \iff A=\frac{ik}{(1-ikL)} $

Ainsi $ \phi_0(x)=(\frac{ik}{(1-ikL)})x+1 $

Ordre 1

Puis à l'ordre 1:

$ \phi_{1,xx}(x)={-k^2}\phi_0(x) $

donc par double intégration on a :

$ \phi_1(x) = -k^2\int\phi_0dxdx +Ax+B $.

Avec pour conditions aux limites :

$ \phi_1^0=0 $

et

$ \phi_{1, x}^L={ik}\phi_1^L $

on a

$ B=0 $

et

$ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $

Calcul de A :

$ \phi_1(x)= -k^2(({ik}/({1-ikL})6)x^3+x^2/2+Ax $

en x=L:

$ \phi_{1, x}^L={ik}\phi_1^L $

$ \iff \frac{ikL^2}{(1-ikL)^2}+L+A=\frac{ik(ikL^3)}{(1-ikL)*6}+\frac{L^2}{2}+AL $

en isolant A dans l'équation on retrouve :

$ A=\frac{-k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2} $

On a donc :

$ \phi_{1}(x)= -\frac{k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2}x-k^2(\frac{ik}{6(1-ikL)})x^3+\frac{x^2}{2} $

Ordre supérieur

On peut ensuite modéliser les ordres suivants grâce à WXMaxima A partir des valeurs numériques suivantes :

$ k=\frac{1}{100} $ (nombre d'onde en m^-1)

$ H=40 $ (profondeur en m)

$ c=\sqrt{gH} $ (célérité de l'onde en m/s)

$ \lambda=\frac{2\pi}{k} $ (longueur d'onde en m)

$ L=2\lambda $ (longueur du domaine en m)

Etude de sensibilité

On regarde la convergence de la méthode par homotopie en fonction du produit kL.

Cas kL=0,25

Cas kL=1

Cas kL=2

Cas N°2

Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec entrée par l'aval d'une onde de fréquence unitaire et une condition de flux aval $ \phi_{x} =ik(2−\phi) $ et réflexion totale amont $ \phi_{x}=0 $.

Méthode analytique

Comme pour le cas N°1, l'équation de Berkhoff à une dimension s'écrit $ \phi_{xx} + k^2\phi = 0 $

Ce qui nous donne comme forme pour $ \phi $ : $ \phi(x) = Ae^{ikx} + Be^{-ikx} $

On peut déterminer les constantes A et B avec les conditions initiales de ce cas.

$ \phi_{x}(0) = ik(2 - \phi(0)) \iff ik(A - B) = ik(2 - A - B) $

$ \iff A = 1 $

Et

$ \phi_{x}(L) = 0 \iff ik(Ae^{ikL} - Be^{-ikL}) = 0 \iff B = e^{2ikL} $

Ainsi

$ \phi(x)= e^{ikx} + e^{2ikL}e^{-ikx} $

La solution réelle associée à cette fonction est $ h(x) = cos(kx) + cos(2kL+kx) $

Méthode par homotopie

En procédant de la même manière que dans le cas 1 on retrouve comme relation d'homotopie :

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+...)]=0 $

Ordre 0

Tout d'abord, à l'ordre 0:

$ \phi_{0,xx}(x)=0 $

Par intégration on a :

$ \phi_0(x)=Ax+B $

Avec les conditions aux limites :

$ \phi_{0,x}^0=ik(2-\phi) $ et

$ \phi_{0, x}^L=0 $

On a :

$ A = 0 $

et

$ B = 2 $

Donc

$ \phi_0(x)=2 $

Ordre 1

Ensuite, pour l'ordre 1:

On a

$ \phi_{1,xx}(x) = -k^{2}\phi_0(x) $

donc

$ \phi_1 (x) = -k^2x^2 + Ax + B $

Avec les conditions initiales on trouve pour A et B :

$ A = 2k^2L $ et $ B = 2ikL $

Donc

$ \phi_1 (x) = - k^2x^2 + 2k^2Lx + 2ikL $

Ordres supérieurs

Pour les ordres supérieurs on effectue les calculs sur maxima jusqu'au rang n.

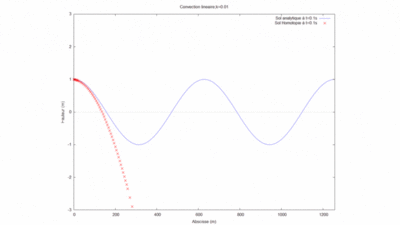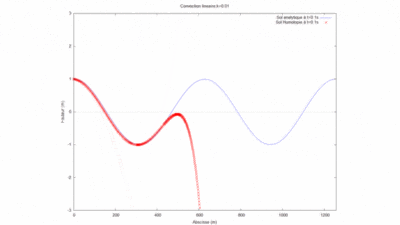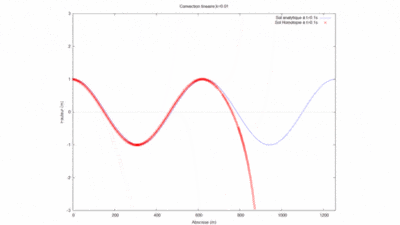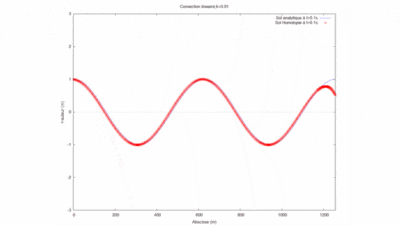
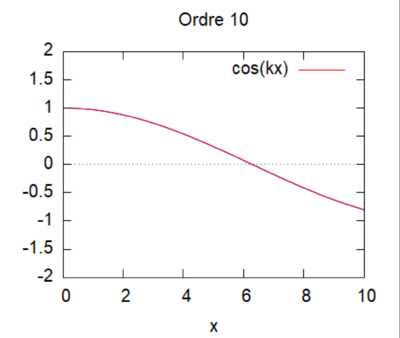
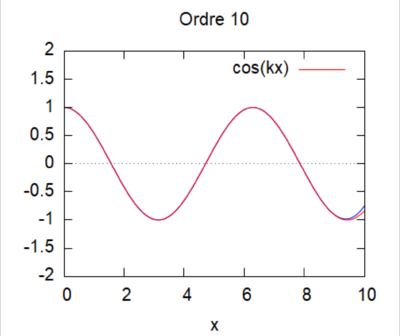
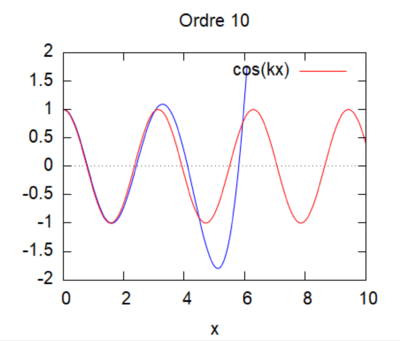
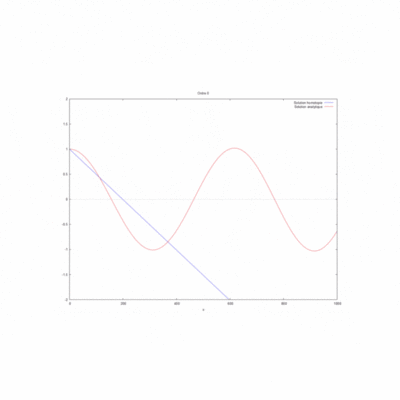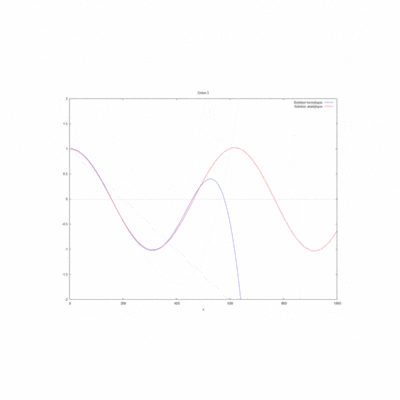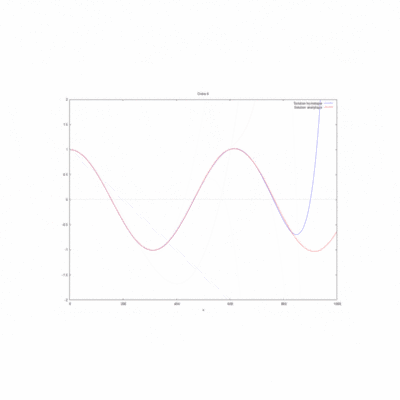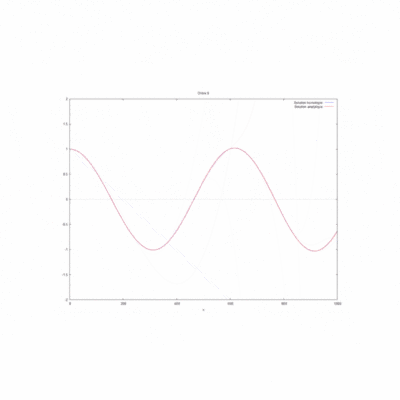
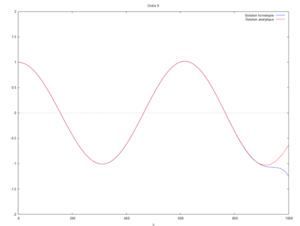
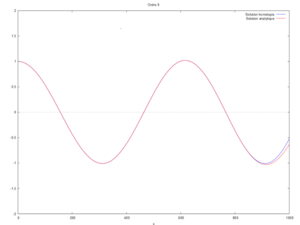
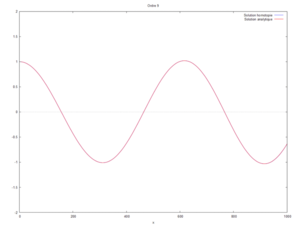
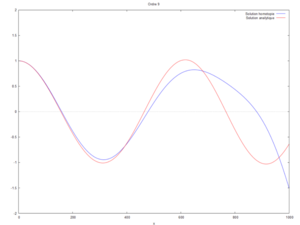
On peut ici voir la solution analytique comparée à la solution par homotopie selon son ordre ( de 0 à 10) :

Etude de sensibilité

On a modifié la valeur du produit kL pour comparer les courbes produites par homotopie à l'ordre 12 avec la solution analytique.

Pour kL = 0,1 :

Pour kL = 0,5 :

Pour kL = 1 :

Cas N°3

Dans ce cas, nous nous placerons dans un domaine monodimensionnel plat de longueur L avec une pente de fond constante (s=cst). L'entrée se fait par l'aval avec une onde de fréquence unitaire $ \phi_{x} =ik(2−\phi) $ et la sortie en amont $ \phi_{x}(x=L)=ik\phi(x=L) $.

Méthode analytique

Le problème est complexifié puisque H(x) n'est plus égal à $ H_0 $ mais à $ H_0-sx $.

On a toujours $ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $ mais avec $ C=C_g=\sqrt{gH(x)} $

Soit

$ {\displaystyle H(x)\frac{\partial^2 \phi}{\partial x^2} -\frac{\partial \phi}{\partial x} + k^2H(x) \phi = 0} $

Nous utilisons le changement de variable : $ z=H_0-sx $.

Et nous prenons: $ s = \frac{1/200} \ $.

Nous nous intéressons au cas $ k=ko\sqrt{Ho/H(x)} $.

Soit l'équation à résoudre :

$ (H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi=0 $

On cherche une solution de la forme de l'équation de Bessel, c'est à dire de la forme : $ z^2\phi_{zz}+z\phi_{z}+(\dfrac{k^2}{s^2})z^2\phi=0 $

$ \phi(z)=AJ_0(\dfrac{k}{s}z)+BY_0(\dfrac{k}{s}z) $

Avec les conditions limites :

$ \phi(x=0)=1 $ et $ \phi_x(x=L)=ik \phi(x=L) $

Ce qui donne avec le changement de variable :

$ \phi(z=H_0)=1 $

et

$ \phi_z(z=H_0-sL)=ik \phi(z=H_0-sL) $

On obtient au final :

$ {\phi(z)=\frac{iY_0^L - Y_1^L}{J_0^0(iY_0^L - Y_1^L) + Y_0^0 (J_1^L-i J_0^L)} J_0 (2 \alpha \sqrt{z}) + \frac{J_1^L - i J_0^L}{J_0^0 (i Y_0^L-Y_1^L) + Y_0^0 (J_1^L - i J_0^L)} Y_0 (2 \alpha \sqrt{z})} $

Méthode par homotopie

Soit la relation d'homotopie suivante : $ (1-p)\phi_{xx}+p((H_0-sx)\phi_{xx}-s\phi_{x}+k^2(H_0-sx)\phi)=0 $

En procédant de la même manière que les cas précédent on a la relation d'homotopie :

$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...)+p(H_0-sx)[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+...-s(\phi_{0,x}+p\phi_{1,x}(x)+p^2\phi_{2,x}(x)+...+k^2(H_0-sx)(\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+...)]=0 $

Ordre 0

$ \phi_{xx}=0 $ donc on a $ \phi_0=Ax+B $

et avec les conditions limites on détermine A et B et on trouve :

$ \phi_0=\frac{ik}{1-ikL}x+1 $

Ordre 1

$ \phi_{1,xx}(x) - \phi_{0, xx}(x) + (H_0 -sx)\phi_{0, xx}(x) - s\phi_{0,x}(x) + k^2(H_0-sx)\phi_0(x) = 0 $

Or $ k^2(H_0-sx)= k_0^2H_0 $

Donc on a

$ \phi_{1,xx}(x) - \phi_{0, xx}(x) + (H_0 -sx)\phi_{0, xx}(x) - s\phi_{0,x}(x) + k_0^2H_0\phi_0(x) = 0 $

On obtient avec une première intégration :

$ \phi_{1,x}(x) = -{k_0}^{2}{H_0}\frac{ik}{1-ikL}\frac{x^2}{2} + \frac{ik}{1-ikL}sx - {k_0}^2{H_0}x + A $

Et par une deuxième intégration on a :

$ \phi_1(x) = -{k_0}^{2}H_0\frac{ik}{1-ikL}\frac{x^3}{6} + \frac{ik}{1-ikL}s\frac{x^2}{2} – {k_0}^{2}{H_0}\frac{x^2}{2} + Ax + B $

Ordres supérieurs

On continue le processus sur n itérations.

La simulation sur WXMaxima nous donne pour le produit kL=1 et pour les ordres 0 à 9 le gif suivant :

Etude de sensibilité

On observe qu'en modifiant la valeur du produit kL , on remarque que la méthode par homotopie converge plus vite pour un kL = 1.

kL = 0,1

kL = 0,5

kL = 1

kL = 2

Cas N°4

Dans ce cas nous nous intéressons à une vague sphérique générée par une source sinusoïdale. Nous étudions la surface libre dans un domaine infini en grande profondeur. Cette source est ponctuelle, appliquée autour d'un cercle r_0 centré sur un domaine circulaire de rayon R qui laisse sortir librement cette onde en r=R. L'équation de Berkhoff se simplifie alors en équation d'Helmholtz et s'exprime en coordonnées polaires. Les conditions sont :

$ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $

Et de manière simplifiée, sachant que le problème est caractérisé par une symétrie de révolution, il y a indépendance de $ \theta $ :

$ \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r=r_0}=1, \\\phi_r^{r=R}=ik\phi^{r=R}. \end{cases} $

avec $ r_0=1m $, $ R=100m $ et $ k=0.1m^{-1} $.

Méthode analytique

Les solutions génrales de cette équation sont de la forme :

$ \phi(r)=AJ_0(r)+BY_0(r) $

Avec  : $ J_0 $ : fonction de Bessel de 1ère espèce

$ Y_0 $ : fonction de Bessel de 2ème espèce

A et B : constante

A partir des conditions limites, on a :

$ \bullet\ AJ_0(r_0)+BY_0(r_0)=1 $

$ \bullet\ AJ_0'(R)+BY_0'(R)=ik\ (AJ_0(R)+BY_0(R)) $

Or

$ \bullet\ \displaystyle\frac{\partial r^nJ_n(r)}{\partial r} = r^nJ_{n-1}(r) $

$ \bullet\ J_{-1}(r) = -J_1(r) $

On a donc :

$ \bullet\ A = \displaystyle\frac{Y_1(R) + ikY_0(R) }{Y_1(R)J_0(r_0) + ikY_0(R)J_0(r_0) - J_1(R)Y_0(r_0) - ikJ_0(R)} $

$ \bullet\ B = \displaystyle\frac{1 }{Y_0(r_0)} \left(1-J_0(r_0)\frac{Y_1(R) + ikY_0(R) }{Y_1(R)J_0(r_0) + ikY_0(R)J_0(r_0) - J_1(R)Y_0(r_0) - ikJ_0(R)}\right) $

Soit

$ \bullet\ \displaystyle\phi(r)=\frac{Y_1(R) + ikY_0(R) }{Y_1(R)J_0(r_0) + ikY_0(R)J_0(r_0) - J_1(R)Y_0(r_0) - ikJ_0(R)}J_0(r)+\frac{1 }{Y_0(r_0)}\left(1-J_0(r_0)\frac{Y_1(R) + ikY_0(R) }{Y_1(R)J_0(r_0) + ikY_0(R)J_0(r_0) - J_1(R)Y_0(r_0) - ikJ_0(R)}\right)Y_0(r) $

Méthode par homotopie

Nous avons la relation d'homologie suivante : $ (1-p)\phi_{rr}+p(\phi_{rr}+\frac{1}{r}.\phi_{r}+k^2\phi)=0 $

Nous utilisons à nouveau la décomposition en séries entières: $ \phi(r,p) $
Ainsi que sa seconde dérivée : $ \phi_{0,rr}(r)+p\phi_{1,rr}(r)+p^2\phi_{2,rr}(r)+p^3\phi_{3,rr}(r)+... $

Ce qui donne: $ (1-p)(\phi_{0,rr}(r)+p\phi_{1,rr}(r)+p^2\phi_{2,rr}(r)+p^3\phi_{3,rr}(r)+...)+p[\phi_{0,rr}(r)+p\phi_{1,rr}(r)+p^2\phi_{2,rr}(r)+p^3\phi_{3,rr}(r)+...+k^2(\phi_0(r)+p\phi_0(r)+p^2\phi_2(r)+p^3\phi_3(r)+...)]=0 $

Ordre 0

On a pour ce cas p = 0 On a la relation : $ \phi_0,rr = 0 \Leftrightarrow \phi_0 = Ar+B $

A l'aide des conditions aux limites :

- $ \phi_0(r=r_0) = 1 \Leftrightarrow Ar_0+B = 1 $

- $ \phi_r(r=R) = ik \phi(r=R) \Leftrightarrow A = ik(AR+B) $

On a donc : $ A = \frac{ik}{1+ik(r_0-R)} $ et $ B = \frac{1-ikR}{1+ik(r_0-R)} $

On en déduit alors : $ \phi_0 = \frac{ik}{1+ik(r_0-R)} r + \frac{1-ikR}{1+ik(r_0-R)} $

Ordre 1

On a pour ce cas la relation :

$ \phi_{1,rr} + \frac{1}{r}\phi_{0,r} + k^2\phi_0 = 0 \leftrightarrow \phi_1(r) + \frac{ik}{1+ik(r_0-R)}r(\ln(r)-1) + \frac{ik}{6(1+ik(r_0-R))}r^3 + \frac{1-ikR}{2(1+ik(r_0-R))}r^2 + Cr + D = 0 $

A l'aide des conditions aux limites suivantes :

- $ \phi_1(r=r_0) = 1 $

- $ \phi_r(r=R) = ik \phi(r=R) $

On en déduit donc :

- $ C = \frac{1}{1+ik(r_0-R)}(ik(AR(\ln(R)-1)\frac{ik}{1+ik(r_0-R)}+\frac{ik}{6(1+ik(r_0-R))}R^3 + \frac{1-ikR}{2(1+ik(r_0-R))}R^2 - A\ln(R) - \frac{ik}{2(1+ik(r_0-R))}R^3-\frac{1-ikR}{2(1+ik(r_0-R))}R)-A\ln(R) - \frac{ik}{2(1+ik(r_0-R))}R^3-\frac{1-ikR}{2(1+ik(r_0-R))}R) $

- $ D = \frac{1}{1+ik(r_0-R)}(A\ln(R) + \frac{ik}{2(1+ik(r_0-R))}R^3+\frac{1-ikR}{2(1+ik(r_0-R))}R - ik(AR(\ln(R)-1)\frac{ik}{1+ik(r_0-R)}+\frac{ik}{6(1+ik(r_0-R))}R^3 + \frac{1-ikR}{2(1+ik(r_0-R))}R^2 - Ar_0(\ln(r_0)-1)\frac{ik}{1+ik(r_0-R)}-\frac{ik}{6(1+ik(r_0-R))}r_0^3 - \frac{1-ikR}{2(1+ik(r_0-R))}r_0^2))r_0 -Ar_0(\ln(r_0)-1)\frac{ik}{1+ik(r_0-R)}-\frac{ik}{6(1+ik(r_0-R))}r_0^3 - \frac{1-ikR}{2(1+ik(r_0-R))} $

Ordre supérieur

Pour trouver la forme des vagues pour les ordres suivants on peut utiliser WXMaxima. Malheureusement, nous n'avons pas réussi à modéliser.

Etude de sensibiité

N/A

Conclusion

L'intérêt de la méthode d'homotopie est qu'elle nous permet de simuler tous les cas de figures et tous les profils de vague possibles, y compris les plus complexes, irrésolvables analytiquement.

De nos jours, et cela va s'accentuer avec les changements climatiques, la modélisation de la houle est un outil très important. En effet, elle nous permet d'anticiper la forme et donc l'impact des vagues sur les côtes, ce qui permet de prévoir les infrastructures nécessaires à construire pour empêcher les dégâts.

On pourrait donc désormais s'intéresser aux moyens les plus efficaces pour réduire ou stopper la dégradation de nos côtes et de nos estuaires.