Utilisateur:Jean-Michel Tanguy/SujetENTPE2023/B03
- Projet modélisation 2022-2023 : Impact du changement climatique sur les côtes et dans les estuaires
- Lucile ANCEY-SERVAIRE, Aurélie KARTODOWIRJO, Nina KHODJA
- Projet modélisation 2022-2023 : Impact du changement climatique sur les côtes et dans les estuaires
Contexte
Aujourd’hui, les effets du changement climatique sont à l’origine de la dégradation des zones côtières. Face à ce danger, adapter les territoires littoraux devient indispensable. Pour trouver des solutions adaptées, il est nécessaire de quantifier l’impact du changement climatique sur le littoral. Pour cela, nous nous intéresserons à l’influence de la houle qui constitue un des principaux agents de l’érosion côtière, à travers la mise en scène d'un reportage scientifique.
Lien vers la vidéo du reportage : https://www.dailymotion.com/video/x8le9dw
Lien vers la vidéo de l'explication du modèle mathématiques : https://www.dailymotion.com/video/x8leaaw
Présentation du projet et des outils de modélisation
Dans ce projet, nous modélisons les mouvements de la houle grâce à l’Équation aux Dérivées Partielles (EDP), donnée par le modèle de Berkhoff, que nous résoudrons numériquement par la méthode de l’homotopie avec différentes conditions limites.
Modèle de Berkhoff
Pour modéliser la houle, nous utilisons le modèle de Berkhoff qui a pour expression : $ \nabla.(CC_g\nabla \phi)+k^2CC_g\phi=0 $
Avec : $ \phi $ : le potentiel, k : le nombre d’onde, fonction de la profondeur H et de la fréquence $ \omega $ par la relation $ \omega^2=gk \tanh(kH) $, C : la célérité de l’onde, Cg : la célérité de groupe des vagues.
Cette EDP modélise la réflexion, la réfraction ou la diffraction des ondes sur les digues.
Pour simplifier le problème, nous nous placerons dans le domaine des ondes longues qui implique $ C=C_g=\sqrt{gH} $. L’équation de Berkhoff devient : $ \nabla \phi+k^2\phi=0 $.
La relation entre le potentiel $ \phi $ et la hauteur de houle dans le temps $ h(x,t) $ est donnée par : $ h(x,t)=\Re \left (\phi e^{-i\omega t} \right ) $.
Homotopie
La résolution analytique de l’équation de Berkhoff donne la solution réelle, cependant cette méthode peut être difficile à exécuter en fonction des conditions appliquées pour modéliser des formes de littoral complexes. C’est pourquoi nous cherchons à approximer la solution par la méthode HAM « Homotopie Perturbation Method ». Celle-ci consiste à approcher une solution initiale connue par une fonction polynomiale qu’on suppose proche de la solution recherchée pour toutes les valeurs d’un paramètre d’homotopie p compris entre 0 et 1.
La méthode d’homotopie consiste à résoudre l’équation différentielle suivante : $ L(u(x)=f(x)+N(u(x), x \in \Omega $
Avec les conditions limites : $ B(u,u_n=0), x \in \Gamma $ L est un opérateur linéaire, N un opérateur non-linéaire f les termes complémentaires de l’équation.
Dans notre cas, on utilisera l'homotopie de Liao définit par : $ (1-p)\left[ L(U(x,t);p)-L(u_0(x,t)) \right ] +H(p)\left[ L(U(x,t);p)-N(U(x,t),p)-f(x) \right] $
Avec $ u_0 $ une estimation initiale de la solution.
Lorsque p = 0 nous retrouvons la solution initiale connue $ U = u_0 $ et lorsque p = 1, nous retrouvons la solution exacte vers laquelle on veut tendre.
La transformation de p de 0 à 1 qui conduit U(x) de la solution estimée à la solution exacte provient de la transformation de U(x) en série de Taylor : $ U(x)=u_0(x)+\sum_{m=1}^\infty u_m(x)p^m $ avec $ u_m(x)=\dfrac{1}{m!}\dfrac{\partial^mU(x,t;p)}{\partial p^m}\Bigr]_{p=0} $
Hypothèses simplificatrices :
Dans notre cas pour éviter les non-linéarités, on fait l’hypothèse propre à la méthode HAM : $ H(p)=1 $. De plus, on partira d’une solution initiale nulle et on prendra pour opérateur linéaire L, la dérivée seconde.
La relation d’homotopie devient : $ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $
Cas 1 : Canal monodimensionnel plat avec sortie libre en amont
Dans le cas n°1, nous considérons un canal monodimensionnel plat, de longueur L de conditions limites :
À l’aval, en x = 0 : Condition de Dirichet $ \phi(x=0)=1 $ En amont, en x = L : Condition de Robin $ \phi_x(x=L)=ik\phi(x=L) $
Résolution analytique
Résoudre l’équation du modèle de Berkhoff en 1D, $ \phi_{xx}+k^2\phi=0 $ revient à résoudre l’équation caractéristique suivante : $ r^2+k^2=0 $ Avec $ r=\pm{ik} $
D’où la solution est de la forme $ \phi(x)={A}e^{ikx}+{B}e^{-ikx} $, avec A et B des constantes réelles à déterminer.
D’après les conditions limites, on a : $ \phi(x=0)=A+B=1 $ $ \phi_x(x=L)=ik\phi(x=L) $ $ \iff {ikA}e^{ikL}-{ikB}e^{-ikL} = {ik}({A}e^{ikx} + {B}e^{-ikx}) $
Ce qui donne A = 1 et B = 0.
Donc le potentiel complexe vaut : $ \phi(x)=e^{ikx} $
Pour avoir la hauteur de la houle dans le temps, on utilise : $ h(x,t) = \Re\left(\phi e^{-i\omega t}\right) $. En remplaçant $ \phi $ trouvé précédemment : $ h(x,t)=\Re\left(e^{i(kx-\omega t)}\right) $.
On obtient donc : $ \boxed{{\color{green}h(x,t)=\cos(kx–\omega t)}} $
Résolution par homotopie
On rappelle que la relation d’homotopie est la suivante : $ (1-p)\phi_{xx}+p(\phi_{xx}+k^2\phi)=0 $
En injectant la décomposition en série entière de $ \phi(x, p) $ : $ \phi(x,p)=\phi_0(x)+p\phi_1(x)+p^2\phi_2(x)+p^3\phi_3(x)+... $ et sa seconde dérivée $ \phi_{0, xx}(x) $ : $ \phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+... $
On obtient : $ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...)]=0 $
- Ordre 0 :
$ \phi_{0,xx}(x)=0 $ $ \Rightarrow \phi_0(x)=Ax+B $ par intégration.
D’après les conditions limites, on a : $ \phi_0^0=B=1 $
$ \phi_{0, x}^L=A={ik}\phi_0^L $ avec $ \phi_0^L=AL+1 $
Donc : $ {\color{green}\phi_{0}(x)=\left(\frac{ik}{1-ikL}\right){x}+1} $
- Ordre 1 :
$ \phi_{1,xx}(x)={-k^2}\phi_0(x) $ $ \Rightarrow \phi_1(x) = -k^2\int\phi_0dxdx +Ax+B $.
D’après les conditions limites, on a : $ \phi_1^0=B=0 $
$ \phi_{1, x}^L=-k^2(\frac{ikL^2}{(1-ikL)2} + L)+A ={ik}\phi_1^L $ avec $ \phi_1^L=-k^2(\frac{ikL^3}{(1-ikL)6} + \frac{L^2}{2})+AL $
Donc : $ {\color{green}\phi_{1}(x)= - \frac{k^2L(k^2L^2+3ikL-3)}{3(1-ikL)^2}x-k^2\left(\frac{ik}{6(1-ikL)}x^3+\frac{1}{2}x^2\right)} $
- Ordre 2 :
On utilise les valeurs suivantes : $ k=\dfrac{1} {100} $ (nombre d'onde en m-1), $ H=40 $ (profondeur en m), $ c=\sqrt{gH} $ (célérité de l'onde en m/s), $ \lambda=\dfrac{2\pi}{k} $ (longueur d'onde en m), $ L=2\lambda $ (longueur du domaine en m).
$ \phi_{2,xx}(x)={-k^2}\phi_1(x) $ $ \iff \phi_2(x) = -k^2\int\phi_1dxdx+Ax+B $.
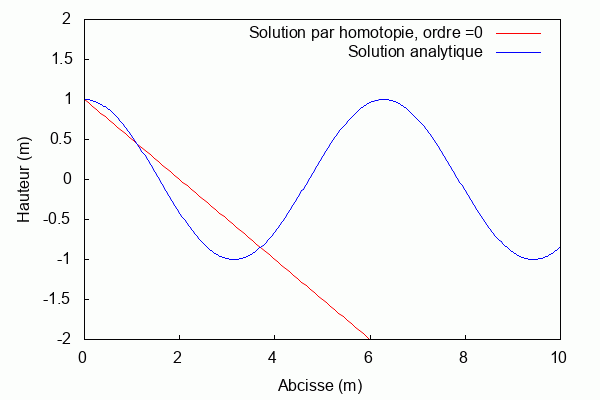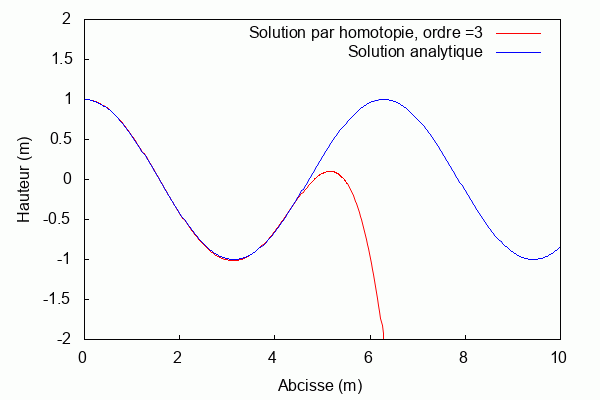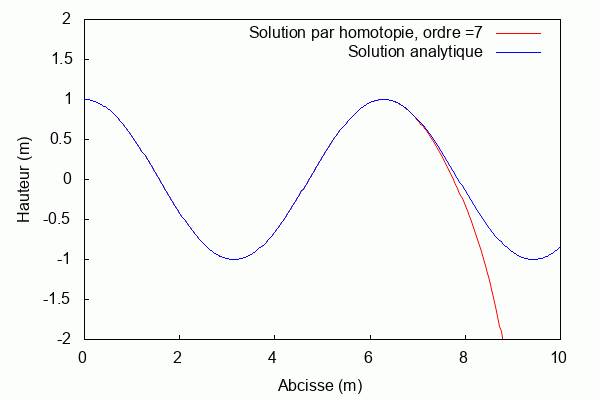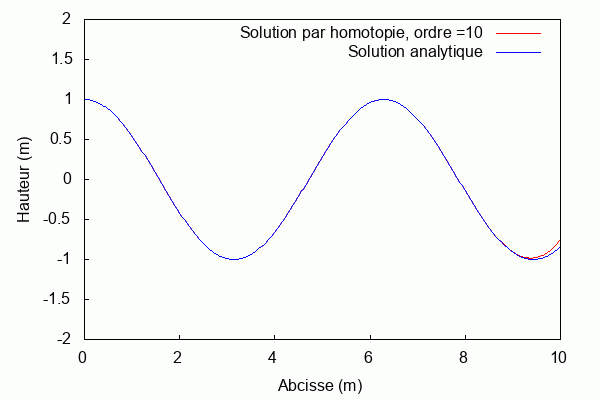
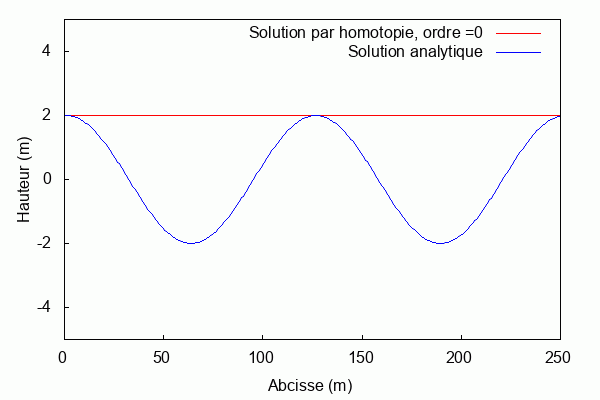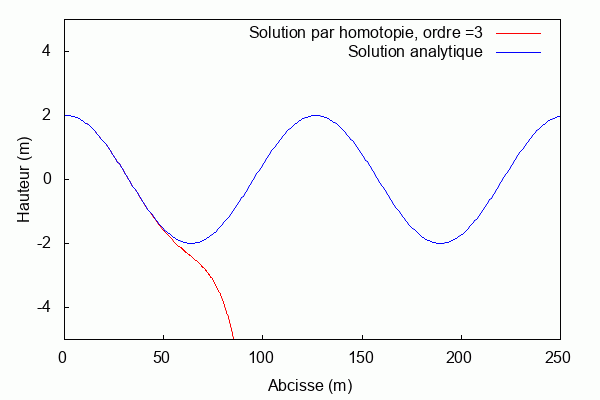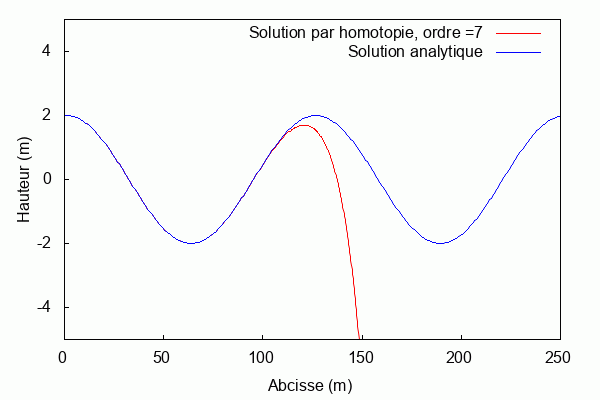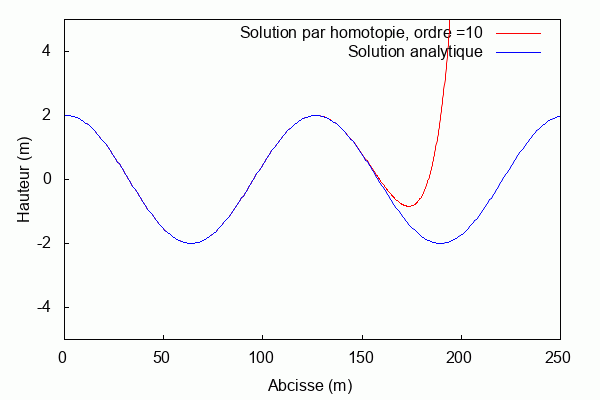
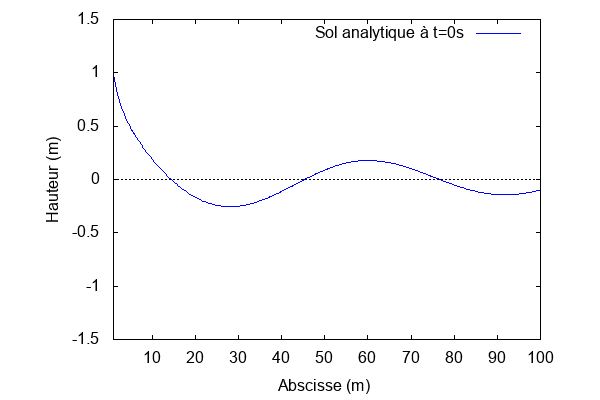
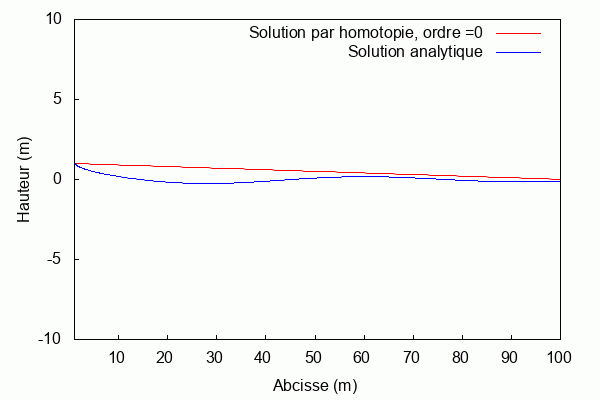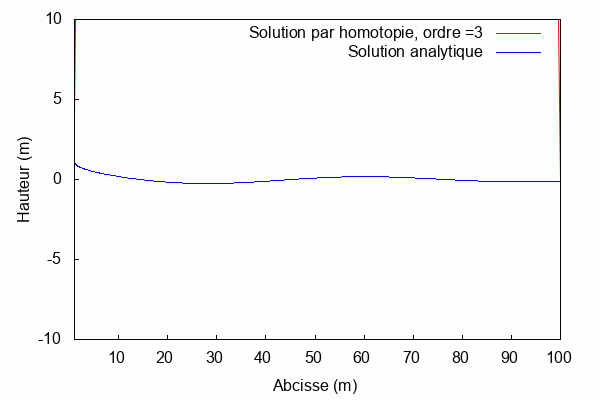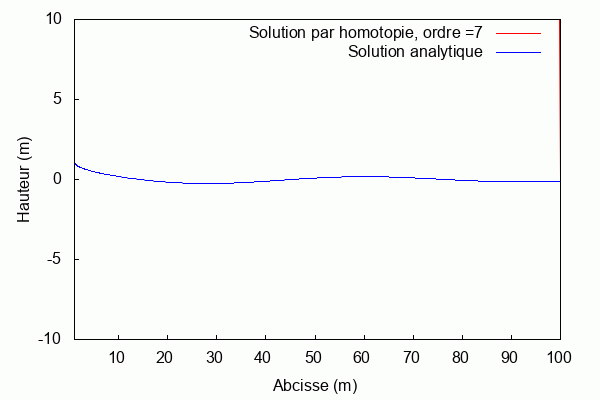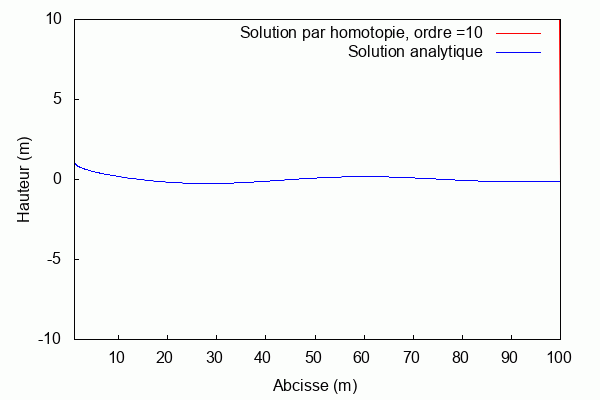
Pour k = 1 et L = 1 :
Étude de sensibilité
Par définition, l’étude de sensibilité permet de quantifier la sensibilité d’une grandeur aux variations d’un paramètre caractéristique du système. Dans ce projet, nous ferons varier la grandeur k associée au nombre d’onde. En fixant les autres paramètres, on peut s’intéresser à la manière dont cette variable influence la convergence de la solution par homotopie vers la solution analytique.
$ \textbf{Pour k = 1 et L = 1 :} $

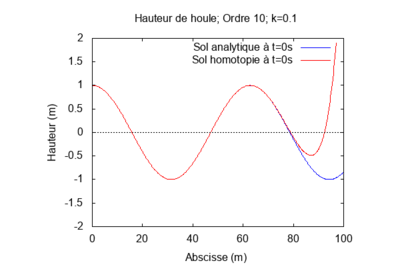
$ \textbf{Pour k = 0.1 et L = 1 :} $
$ \textbf{Pour k = 2 et L = 1 :} $
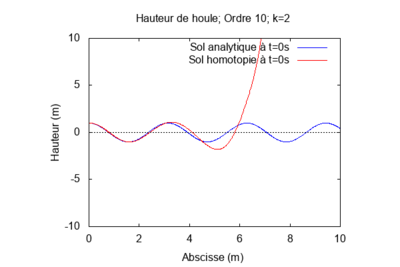
Lorsque le produit kL = 1, la solution par homotopie converge rapidement vers la solution analytique. Au contraire, lorsqu'il s'en éloigne la solution par homotopie diverge.
Cas 2 : Canal monodimensionnel plat avec une condition de flux en aval et une réflexion totale en amont
Dans le cas n°2, nous considérons un canal monodimensionnel plat, de longueur L de conditions limites :
À l’aval, en x = 0 : Condition de Robin $ \phi_x(x=0)=ik(2-\phi) $ En amont, en x = L : Condition de Dirichlet $ \phi_x(x=L)=0 $
Résolution analytique
Résoudre l’équation du modèle de Berkhoff en 1D, $ \phi_{xx}+k^2\phi=0 $ revient à résoudre l’équation caractéristique suivante : $ r^2+k^2=0 $ Avec $ r=\pm{ik} $
D’où la solution est de la forme $ \phi(x)={A}e^{ikx}+{B}e^{-ikx} $, avec A et B des constantes réelles à déterminer.
D’après les conditions limites, on a : $ \phi(x=0)=A+B=ik(2-\phi) $ $ \phi_x(x=L)=0 $ $ \iff {ikA}e^{ik L}-{ikB}e^{-ik L} = {ik}({A}e^{ikx} + {B}e^{-ikx}) $
Ce qui donne $ A = 1 $ et $ B = e^{2ikL}. $
Donc le potentiel complexe vaut : $ \phi(x)=e^{ikx}+e^{ik(2L-x)} $
Pour avoir la hauteur de la houle dans le temps, on utilise : $ h(x,t) = \Re\left(\phi e^{-i\omega t}\right) $. En remplaçant $ \phi $ trouvé précédemment : $ {h(x,t)} =\Re \left(e^{i(kx- \omega t)} +e^{i(k(2L-x)- \omega t)}\right) $.
On obtient donc $ \boxed{{\color{green} h(x,t)=\cos(kx–\omega t)+\cos(k(2L-x)-\omega t)}} $
Résolution par la méthode d'homotopie
De la même manière que pour la cas 1, la relation d’homotopie est la suivante :
$ (1- p)(\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...)+p[\phi_{0,xx}(x)+p\phi_{1,xx}(x)+p^2\phi_{2,xx}(x)+p^3\phi_{3,xx}(x)+...+k^2(\phi_0(x)+p\phi_0(x)+p^2\phi_2(x)+p^3\phi_3(x)+...)]=0 $
- Ordre 0 :
$ \phi_{0,xx}(x)=0 $ $ \Rightarrow \phi_0(x)=Ax+B $ par integration.
D’après les conditions limites, on a : $ \phi_{0, x}^0=B=2 $
$ \phi_{0, x}^L=A=0 $
Donc : $ {\color{green} \phi_0(x)=2} $
- Ordre 1 :
$ \phi_{1,xx}(x)={-k^2}\phi_0(x) $ $ \Rightarrow \phi_1(x) = -k^2\int\phi_0dxdx +Ax+B $.
Par intégration : $ \phi_1(x) = {-k^2}x^2 + Ax + B $
D’après les conditions limites, on a : $ \phi_{1, x}^L={-k^2}2L+A = 0 $ d'où $ A = 2L{k^2} $
$ \phi_{1, x}^0=-ik\phi_{1}^0) $ avec $ \phi_{1}^0 = {-k^2}B et \phi_{1, x}^0 = A $ d'où $ B = 2ikL $
Donc : $ {\color{green}\phi_1(x)= {-k^2}x^2 + 2L{k^2}x + 2ikL} $
- Ordre 2 :
On utilise les valeurs suivantes : $ k=\dfrac{1} {100} $ (nombre d'onde en m-1), $ H=40 $ (profondeur en m), $ c=\sqrt{gH} $ (célérité de l'onde en m/s), $ \lambda=\dfrac{2\pi}{k} $ (longueur d'onde en m), $ L=2\lambda $ (longueur du domaine en m).
$ \phi_{2,xx}(x)={-k^2}\phi_1(x) $ $ \iff \phi_2(x) = -k^2\int\phi_1dxdx+Ax+B $.
Pour k = 0.05 et L = 1 :
Étude de sensibilité
Comme pour le cas précédent, on s'intéresse à la conséquence de la variation du nombre d'onde k sur la convergence de la solution par homotopie vers la solution analytique.
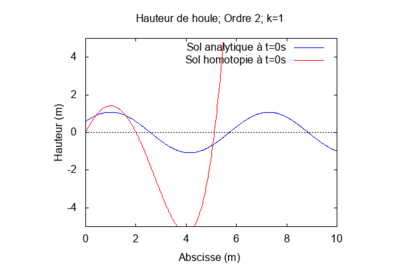
$ \textbf{Pour k = 1 et L = 1 :} $
$ \textbf{Pour k = 0,1 et L = 1 :} $
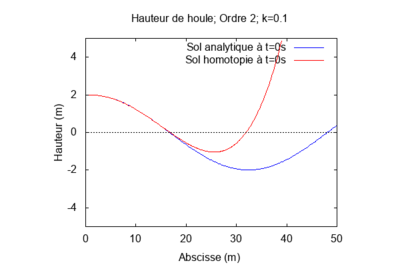
$ \textbf{Pour k = 0,05 et L = 1 :} $

Lorsque le produit kL = 1, la solution par homotopie diverge contrairement au cas précédent. On remarque la solution par homotopie converge rapidement vers la solution analytique quand k est petit. Au contraire, lorsqu'il augmente la solution par homotopie diverge.
Cas 3 : Canal monodimensionnel, avec pente de fond constante et une sortie libre amont
Résolution analytique
Dans le cas n°3, nous considérons un canal monodimensionnel, avec une pente de fond constante $ s $ et une sortie libre en amont, de conditions limites :
À l’aval, en x = 0 : Condition de Dirichlet $ \phi(x=0)=1 $
En amont, en x = L : Condition de Robin $ \phi_x(x=L)=ik\phi(x=L) $
Dans ce cas on a : $ C = C_g = \sqrt{gH(x)}. $
H n’est pas constant, on ne peut pas utiliser le modèle de Berkhoff simplifié comme dans les deux cas précédents.
$ \Delta(CC_g\Delta\phi) + {k}^{2}CC_g\phi = 0 \Leftrightarrow H(x)\phi_{xx} - \phi_x + k^{2}H(x)\phi = 0 $
On appliquera dans les calculs qui suivent le changement de variable $ z = H_{0} -sx $ .
Pour la résolution du cas 3, on considère la pente $ s = \frac{1}{200} $.
Cas 1 : k = k0
Pour $ k = k_0 $ on a : $ \nabla(CC_g\nabla\phi) + {k_0}^{2}CC_g\phi = 0 \Leftrightarrow H(x) \phi_{xx} + \frac{\partial H}{\partial x} \phi_{x} + {k_0}^{2}H(x)\phi = 0 \Leftrightarrow z^2 \frac{\partial^2 \phi}{\partial z^2} + z \frac{\partial \phi}{\partial z} + \left(\frac{k_0 z}{s}\right)^2\phi = 0 $
On reconnaît une équation de type Bessel : $ z^2 \frac{\partial^2 \phi}{\partial z^2} + (2p+1)z \frac{\partial \phi}{\partial z} + (α^2 z^{2r} + β^2 ) \phi = 0 $
avec par identification : $ \left\{ \begin{array}{r c l} p=0 \\ β=0 \\ r = 1 \\ α = \frac{k_0}{s} \end{array} \right. $
La solution de cette équation est :$ \phi = z^{-p} \left( A J_{P/r} (\frac{α x^r}{r}) + B Y_{P/r} (\frac{α x^r}{r} ) \right) $
Avec $ P = \sqrt{p^2 + β^2} $, A et B des constantes à déterminer.
D'où $ \color{green}{ \phi = A J_0(αx) + B Y_0(αx)} $
Soit : $ \color{green}{ \phi = A J_0(α(H-sx)) + B Y_0(α(H-sx))} $
- En $ x=0 $, on a $ z=H_0 $ donc :
$ \phi(x=0) = \phi(z=H_0) = \phi_0 ^{0} = 1 $
D'où : $ \color{green}{\phi_0 ^{0}=A J_0(H) + B Y_0(H) = 1} $
- En $ x=L $ , on a $ z=H_0 -sL $ donc :
$ \frac{\partial \phi}{\partial x} = ik\phi \Leftrightarrow \frac{\partial \phi}{\partial z} = \frac{-ik_0 \phi}{s} $ avec $ \left\{ \begin{array}{ll} J_0' = -J_1 \\ Y_0 = -Y_1 \end{array} \right. $
On a : $ \phi_1 = \frac{\partial \phi}{\partial z} = -A α s J_1 (α(H-sx)) - B α s Y_1 (α(H-sx)) $
Donc $ \color{green}{ \phi_1^L = -\frac{ik_0}{s}A J_0(α(H-sL)) - \frac{ik_0}{s}B Y_0(α(H-sL))} $
$ \color{green}{ \phi_1^L = -A α s J_0(α(H-sL)) - B α s Y_0(α(H-sL))} $
- Détermination de A et B :
D'après les résultats précédents et en posant $ \left\{ \begin{array}{ll} J_0 (αH)= J_0 ^0 \\ Y_0 (αH) = Y_0 ^0 \\ J_1 (α(H-sL)) = J_1 ^L \\ Y_1 (α(H-sL)) = Y_1 ^L \end{array} \right. $ on a :
$ \left\{ \begin{array}{ll} A J_0^0 + B Y_0^0 = 1 \color{blue}{\textrm{ (1) }} \\ A J_1 ^L + B Y_1 ^L = \frac{ik_0}{α s^2} (A J_0^L + B Y_0^L) \color{blue}{\textrm{ (2) }} \end{array} \right. $ $ \Leftrightarrow \left\{ \begin{array}{ll} B J_0^L Y_0^0 - B J_0^0 Y_0^L = J_0^L - \frac{s^2 α}{ik_0}(A J_1^L J_0^0 + B J_0^0 Y_1^L) \textrm{ En faisant } J_0^L \color{blue}{\textrm{ (1) }} \color{black}{ - J_0^0 \frac{s^2 α}{ik_0}} \color{blue}{\textrm{(2)}}\\ A Y_0 ^L J_0^0 - A Y_0 ^0 J_0^L = Y_0^L -\frac{s^2 α}{ik_0} (A J_1^L Y_0^0 + B Y_1^L Y_0^0) \textrm{ En faisant } Y_0^L \color{blue}{\textrm{ (1) }} \color{black}{ - Y_0^0 \frac{s^2 α}{ik_0}} \color{blue}{\textrm{ (2) }} \end{array} \right. $
- $ \Leftrightarrow \color{green}{ \left\{ \begin{array}{ll} A = \frac{1}{C_1} \left(Y_0^L - \frac{s^2 α}{ik_0} Y_1^L Y_0^0 J_0^L \times \frac{J_0^L}{J_0^L Y_0^0 - J_0^L Y_0^L + \frac{s^2 α}{ik_0} J_0^0 Y_1^L} \right)\\ B = \frac{1}{C_2} \left(J_0^L - \frac{s^2 α}{ik_0} J_1^L Y_0^0 \times \frac{Y_0^L}{Y_0^L J_0^0 - Y_0^0 J_0^L + \frac{s^2 α}{ik_0} Y_0^0 J_1^L} \right) \end{array} \right. } $
Avec $ \left\{ \begin{array}{ll} C_1 = Y_0^L J_0^0 - Y_0^0 J_0^L + \frac{s^2 α}{ik_0} J_1^L Y_0^0 -\left(\frac{s^2 α}{ik_0}\right)^2 \left(\frac{J_1^L Y_1^L \left(Y_0^0\right)^2}{J_0^L Y_0^0 - J_0^L Y_0^L + \frac{s^2 α}{ik_0} J_0^0 Y_1^L}\right)\\ C_2 = J_0^L Y_0^0 - J_0^0 Y_0^L + \frac{s^2 α}{ik_0} Y_1^L J_0^0 -\left(\frac{s^2 α}{ik_0}\right)^2 \left(\frac{Y_1^L Y_0^0}{Y_0^L J_0^0 - J_0^L Y_0^0 + \frac{s^2 α}{ik_0} Y_0^0 J_1^L}\right) \end{array} \right. $
On a donc : $ \boxed{ \color{green}{ \phi = \frac{1}{C_1} \left(Y_0^L - \frac{s^2 α}{ik_0} Y_1^L Y_0^0 J_0^L \times \frac{J_0^L}{J_0^L Y_0^0 - J_0^L Y_0^L + \frac{s^2 α}{ik_0} J_0^0 Y_1^L} \right) J_0(α(H-sx)) + \frac{1}{C_2} \left(J_0^L - \frac{s^2 α}{ik_0} J_1^L Y_0^0 \times \frac{Y_0^L}{Y_0^L J_0^0 - Y_0^0 J_0^L + \frac{s^2 α}{ik_0} Y_0^0 J_1^L} \right) Y_0(α(H-sx))}} $
avec C1 et C2 les constantes déterminées ci-dessus.
Cas 2 : k = k0 (H0/H(x))1/2
Pour $ k = k_0\sqrt{\frac{H_0}{H(x)}} $ et en appliquant le changement de variable $ z = H_{0} -sx $ on a : $ H(x)\phi_{xx} - s\phi_x + k^{2}H(x) = 0 \Leftrightarrow (H_{0} - sx) \frac{\partial^2 \phi}{\partial x^2} - s \frac{\partial \phi}{\partial x} + {k_0}^{2}H_{0}\phi = 0 $
Or $ \left\{ \begin{array}{ll} \frac{\partial \phi}{\partial x} = -s\phi_{z} \\ \frac{\partial^2 \phi}{\partial x^2} = s^2\phi_{zz} \end{array} \right. $ donc $ z s^2 \phi_{zz} + s^2\phi_z + {k_0}^{2}H_{0}\phi = 0 $
En posant
$ \alpha^{2} = \left ( \frac{{k_0}^{2}H_{0}}{s^2} \right ) \Leftrightarrow \alpha = \left ( \frac{\sqrt{H_0}{k_0}^{2}}{s} \right ) $
on retrouve une équation du type Bessel de la forme $ z\phi_{zz} + \phi_z + {\alpha}^{2}\phi = 0 $ .
Donc :
$ {\color{green}z\phi_{zz} + \phi_z + {\alpha}^{2}\phi = 0} $ avec $ \alpha^{2} = \left ( \frac{{k_0}^{2}H_{0}}{s^2} \right ) $
On a pour solution de l'équation de Bessel :
- $ \phi(z) = \left( A J_0 (2 \alpha \sqrt{z}) + B Y_0 (2 \alpha \sqrt{z}) \right) $ avec A et B des constantes à déterminer.
- En $ x = 0 $, on a $ z = H_0 $ donc :
$ {\color{green}\phi(x=0) = \phi(z=H_0) = A J_0 (2 \alpha \sqrt{H_0}) + B Y_0 (2 \alpha \sqrt{H_0}) = 1 } $
- En $ x = L $, on a $ z = H_0 - sL = z_L $ donc :
$ \phi_x^L = ik\phi^L $ or $ \frac{\partial \phi}{\partial x} = \frac{\partial \phi}{\partial z} \frac{\partial z}{\partial x} = -s \frac{\partial \phi}{\partial z} $ donc $ \phi_x = -s\phi_z $
D'où : $ -s \phi_z^{z_L} = i k_0 \phi^{z_L} \Leftrightarrow \phi_z^{z_L} = \frac{-i k^L}{s} \phi^{z_L} $ avec $ \left\{ \begin{array}{ll} \phi^L = A J_0 (2 \alpha \sqrt{z_L}) + B Y_0 (2 \alpha \sqrt{z_L}) \\ \phi_z = \frac{- \alpha}{\sqrt{z}} \left( A J_1 (2 \alpha \sqrt{z} + B Y_1 (2 \alpha \sqrt{z}) \right ) \end{array} \right. $
Ainsi $ {\color{green}\phi_z^{z_{L}} = \frac{- \alpha}{\sqrt{z_{L}}} \left( A J_1 (2 \alpha \sqrt{z_L}) + B Y_1 (2 \alpha \sqrt{z_L}) \right )} $.
- Détermination de A et B :
D'après les résultats trouvés précédemment, on a le système d'équations suivant :
$ \left\{ \begin{array}{ll} A J_0 (2 \alpha \sqrt{H_O}) + B Y_0 (2 \alpha \sqrt{H_0})=1 \\ \frac{- \alpha}{\sqrt{z_L}} \left( A J_1 (2 \alpha \sqrt{z_L}) + B Y_1 (2 \alpha \sqrt{z_L})\right) = \frac{-i k_L}{s} \left (A J_0 (2 \alpha \sqrt{z_L} + B Y_0 (2 \alpha \sqrt{z_L})\right ) \end{array} \right. $
$ \Leftrightarrow \left\{ \begin{array}{ll} A J_0 (2 \alpha \sqrt{H_O}) + B Y_0 (2 \alpha \sqrt{H_0}) = 1 \\ A J_1 (2 \alpha \sqrt{z_L}) + B Y_1 (2 \alpha \sqrt{z_L}) = i \left(A J_0 (2 \alpha \sqrt{z_L}) + B Y_0 (2 \alpha \sqrt{z_L})\right ) \end{array} \right. $
En posant $ \left\{ \begin{array}{ll} J_0 (2 \alpha \sqrt{H_0})=J_0^0 \\ Y_0 (2 \alpha \sqrt{H_0})=Y_0^0 \end{array} \right. $ et $ \left\{ \begin{array}{ll} J_1 (2 \alpha \sqrt{z_L})=J_1^L \\ Y_1 (2 \alpha \sqrt{z_L})=Y_1^L \end{array} \right. $ on a :
$ \left\{ \begin{array}{ll} A J_0^0 + B Y_0^0 = 1 \\ A J_1^L + B Y_1^L = i A J_0^L + i B Y_0^L \end{array} \right. $ $ \Leftrightarrow \left\{ \begin{array}{ll} A = \frac{1-B Y_0^0 }{J_0^0} \\ A (J_1^L - i J_0^L) = B(i Y_0^L-Y_1^L) \end{array} \right. $
- $ \Leftrightarrow {\color{green}\left\{ \begin{array}{ll} A = \frac{iY_0^L - Y_1^L}{J_0^0(iY_0^L - Y_1^L) + Y_0^0 (J_1^L-i J_0^L)} \\ B = \frac{J_1^L - i J_0^L}{J_0^0 (i Y_0^L-Y_1^L) + Y_0^0 (J_1^L - i J_0^L)} \end{array} \right.} $
Donc : $ \boxed{ {\color{green}\phi(z)=\frac{iY_0^L - Y_1^L}{J_0^0(iY_0^L - Y_1^L) + Y_0^0 (J_1^L-i J_0^L)} J_0 (2 \alpha \sqrt{z}) + \frac{J_1^L - i J_0^L}{J_0^0 (i Y_0^L-Y_1^L) + Y_0^0 (J_1^L - i J_0^L)} Y_0 (2 \alpha \sqrt{z})}} $
Résolution par homotopie
On a vu dans la résolution analytique, avec le changement de variable $ H(x) = H_0 -sx $, que l'équation de Berkhoff est : $ (H_0 - sx)\phi_{xx} - s\phi_x + k^{2}((H_0 -sx)\phi) = 0 $
Cas 1 : k = k0
La relation d'homotopie devient : $ (1-p)\phi_{xx} + p[(H_0 - sx\phi_{xx} -s\phi_{x} + {k_0}^{2}{H_0 - sx}\phi) = 0 $
Comme dans les cas précédents, on injecte la décomposition en série entière de $ \phi(x,p), \phi_x(x,p) $ et $ \phi_{xx}(x,p) $ :
$ \left\{ \begin{array}{ll} \phi(x,p) = \phi_{0}(x) + p\phi_1(x) + p^{2}\phi_2(x) + ... \\ \phi_x(x,p) = \phi_{0,x}(x) + p\phi_{1,x}(x) + p^{2}\phi_{2,x}(x) ... \\ \phi_{xx}(x,p) = \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^{2}\phi_{2,xx}(x) + ... \end{array} \right. $
Ce qui donne :
$ (1-p)[\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^{2}\phi_{2,xx}(x) + ...] + p[(H_0 -sx)(\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^{2}\phi_{2,xx}(x) + ...) - s(\phi_{0,x}(x) + p\phi_{1,x}(x) + p^{2}\phi_{2,x}(x) + ...) + {k_0}^2(H_0 - sx)(\phi_{0}(x) + p\phi_{1}(x) + p^{2}\phi_{2}(x) + ...)] $
Par identification, comme $ p \ne 0 $, on obtient :
- Ordre 0 :
$ \phi_{0,xx} (x)=0 $ $ \Rightarrow \phi_0(x)=Ax+B $ par intégration, avec A et B des constantes à déterminer.
D’après les conditions limites, on a : $ \phi_0^0=B=1 $ $ \phi_{0, x}^L=A={ik}\phi_0^L $ avec $ \phi_0^L=AL+1 $
Ainsi $ {\color{green}\phi_{0}(x)=\left(\frac{ik}{1-ik_0L}\right){x}+1} $
- Ordre 1 :
$ \phi_{1,xx}(x) + (H_0 - sx) \phi_{0, xx}(x) + s\phi_{0, x}(x) - {k_0}^{2}{H_0 - sx}\phi_0(x) = 0 $
En remplaçant $ \phi_{0, xx}(x), \phi_{0,x}(x) $ et $ \phi_0(x) $, on a :
$ \phi_{1,xx}(x) = s\left(\frac{ik}{1-ikL}\right) - {k_0}^{2}{H_0 - sx}\left(\frac{ik_0 x}{1-ik_0 L} +1\right) $
$ \Rightarrow \phi_{1,x}(x) = \frac{isk_0}{1-ik_0L}x - {k_0}^{2}H_0 x - \frac{i{k_0}^{3}H_0}{2(1-ik_0L)}x^2 + \frac{s{k_0}^2}{2} x^2 + \frac{is{k_0}^2}{3(1-ik_0L)} x^3 + A $
$ \Rightarrow {\color{green} \phi_1(x) = \frac{isk_0}{2(1-ik_0L)}x^2 - \frac{{k_0}^{2}H_0}{2} x^2 - \frac{i{k_0}^{3}H_0}{6(1-ik_0L)}x^3 + \frac{s{k_0}^2}{6} x^3 + \frac{is{k_0}^2}{12(1-ik_0L)} x^4 + Ax + B} $
On trouve A et B avec les conditions limites :
$ \left\{ \begin{array}{ll} \phi_{1}^0 = {\color{green}B = 0 } \\ {\color{green} A = \frac{18isk_0L + 6i{k_0}^3 H_0 L^2 - is{k_0}^2 L^3 - 2i{k_0}^3 H_0 L^3}{12(1-ik_0L)^2} + \frac{{k_0}^2 H_0 L}{1-ik_0L}\left(\frac{sL^2}{6} - \frac{L}{2} - \frac{sL}{2} - 1\right) } \end{array} \right. $
Cas 2 : k = k0 (H0/H(x))1/2
La relation d'homotopie devient : $ (1-p)\phi_{xx} + p(H_0 - sx\phi_{xx} -s\phi_{x} + {k_0}^{2}{H_0}\phi) = 0 $
De la même manière que pour le cas 3, sous-cas 1 ci-dessus, on a :
$ (1-p)[\phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^{2}\phi_{2,xx}(x) + p^{3}\phi_{3,xx}(x) + ...] + p[(H_0 -sx)(\phi_{xx}(x,p) = \phi_{0,xx}(x) + p\phi_{1,xx}(x) + p^{2}\phi_{2,xx}(x) + p^{3}\phi_{3,xx}(x) + ... ) - s(\phi_{0,x}(x) + p\phi_{1,x}(x) + p^{2}\phi_{2,x}(x) + p^{3}\phi_{3,x}(x) + ...) + {k_0}^2{H_0}(\phi_{0}(x) + p\phi_{1}(x) + p^{2}\phi_{2}(x) + p^{3}\phi_{3}(x) + ...)] $
Par identification, comme $ p \ne 0 $, on obtient :
- Ordre 0 :
$ \phi_{0,xx} (x)=0 $ $ \Rightarrow \phi_0(x)=Ax+B $ par intégration.
D’après les conditions limites, on a : $ \phi_0^0=B=1 $ $ \phi_{0, x}^L=A={ik}\phi_0^L $ avec $ \phi_0^L=AL+1 $
Ainsi $ {\color{green}\phi_{0}(x)=\left(\frac{ik}{1-ikL}\right){x}+1} $
- Ordre 1 :
$ \phi_{1,xx}(x) - \phi_{0, xx}(x) + (H_0 -sx)\phi_{0, xx}(x) - s\phi_{0,x}(x) + {k_0}^{2}{H_0}\phi_0(x) = 0 $
En remplaçant $ \phi_{0, xx}(x), \phi_{0,x}(x) et \phi_0(x) $, on a :
$ \phi_{1,xx}(x) = s\left(\frac{ik}{1-ikL}\right) - {k_0}^{2}{H_0}\left(\frac{ik}{1-ikL}\right)x - {k_0}^2{H_0} $
$ \Rightarrow \phi_{1,x}(x) = -{k_0}^{2}{H_0}\left(\frac{ik}{1-ikL}\right)\frac{x^2}{2} + \left(\frac{ik}{1-ikL}\right)sx - {k_0}^2{H_0}x + A $
$ \Rightarrow {\color{green} \phi_1(x) = -{k_0}^{2}H_0\left(\frac{ik}{1-ikL}\right)\frac{x^3}{6} + \left(\frac{ik}{1-ikL}\right)s\frac{x^2}{2} – {k_0}^{2}{H_0}\frac{x^2}{2} + Ax + B} $
On trouve A et B avec les conditions limites :
$ \left\{ \begin{array}{ll} \phi_{1}^0 = {\color{green}B = 0 } \\ {\color{green} A = \frac{k_0^2{H_0}L}{1 – ikL} \left(1-\frac{ik}{2}+\frac{ikL}{2(1-ikL)}+\frac{k^2 L^2}{6(1-ikL)}\right) - \frac{isLk}{(1-ikL)^2} \left(1-\frac{Lk}{2}\right)} \end{array} \right. $
Cas 4 : Vague sphérique générée par une source périodique sinusoïdale
Résolution analytique
Dans le cas n°4, nous considérons une vague sphérique générée par une source périodique sinusoïdale sur une surface libre dans un domaine infini de grande profondeur. La source ponctuelle est appliquée autour d’un cercle de rayon $ r_0 $ et centré sur un domaine circulaire de rayon R qui laisse sortir cette onde libre en r = R.
L’équation de Berkhoff se simplifie en équation de Helmotz : $ \begin{cases} \Delta \phi + k^2\phi=0, \\ \phi^{r_0}=1, \\\phi_r^{R}=ik\phi^{R}. \end{cases} $
En coordonnées polaires, la symétrie de révolution du problème le rend indépendant de $ \theta $. $ \begin{cases} \phi_{rr}+\dfrac{1}{r}\phi_r + k^2\phi=0, \\ \phi^{r_0}=1, \\\phi_r^{R}=ik\phi^{R}. \end{cases} $
avec $ r_0=1m $, $ R=100m $ et $ k=0.1m^{-1} $.
L’équation à résoudre est une équation de type Bessel, traité précedemment dans le cas 3 en coordonnées cartésiennes.
La solution de l’équation est de la forme :
$ {\color{green}\phi(r) = AJ_0(kr) + BY_0(kr)} $ avec A et B des constantes réelles à déterminer avec les conditions limites.
On a pour équation de Berkhoff : $ \phi + k^2\phi=0 $
Les conditions limites deviennent :
$ \begin{cases} (1) \phi(r=r_0) = AJ_0(kr_0)+BY_0(kr_0), \\ (2) \phi_1(r=R) = ik\phi(r=R) \end{cases} $ avec $ \phi(r=R) = A{J_0}(kR) + B{Y_0}(kR) $
Comme $ \phi_1(r) = -kAJ_1(kr) - kBY_1(kr) $ alors $ \phi_1(r=R) = -kAJ_1(kR) - kBY_1(kR) $
D'où $ (2) $ devient : $ -k(AJ_1(kr) + BK_1(kr)) = ik(AJ_0(kR) + BY_0(kR)) \iff -AJ_1(kR) - BY_1(kR) = iAJ_0(kR) + iBY_0(kR) $
$ \begin{cases} AJ_0(kr_0) + BY_0(kr_0) = 1, \\ -AJ_1(kR) - BY_1(kR) = iAJ_0(kR) + iBY_0(kR) \end{cases} $
On trouve :
$ {\color{green} B = \frac{1-AJ_0(kr_0)}{Y_0(kr_0)} } $
avec $ {\color{green} A = \frac{Y_1(kR) + iY_0(kR)}{J_0(kr_0)(Y_1(kR) + iY_0(kR)) - Y_0(kr_0)(J_1(kR) + iJ_0(kR))} } $
Donc : $ \boxed{ {\color{green} \phi(r) = \frac{Y_1(kR) + iY_0(kR)}{J_0(kr_0)(Y_1(kR) + iY_0(kR)) - Y_0(kr_0)(J_1(kR) + iJ_0(kR))} J_0(kr) - \frac{1}{Y_0(k r_0)}\left(1-\frac{Y_1(kR) + iY_0(kR)}{J_0(kr_0)(Y_1(kR) + iY_0(kR)) - Y_0(kr_0)(J_1(kR) + iJ_0(kR))} J_0(kr_0)\right) Y_0(kr)}} $
Résolution par la méthode d’homotopie
Dans le cas polaire, l’équation de Berkhoff est modifié puisque la symétrie de révolution induit une équation indépendante de $ \theta $ : $ \Delta\phi + k^{2}\phi = \phi_{rr} + \frac{1}{r}{\phi_r} + k^{2}\phi = 0 $
Donc la relation d’homotopie devient : $ (1-p)\phi_{rr} + p(\phi_rr + \frac{1}{r}\phi_r + k^{2}\phi) = 0 $
Comme dans le cas précédent, on injecte la décomposition en série entière de $ \phi(r, p), \phi_{r}(r,p) et \phi_{rr}(r,p) $ :
$ \phi(r,p) = \phi_{0}(r) + p\phi_{1}(r) + p^{2}\phi_{2}(r) + p^{3}\phi_{3}(r) + … $
$ \phi_{r}(r,p) = \phi_{0,r}(r) + p\phi_{1,r}(r) + p^{2}\phi_{2,r}(r) + p^{3}\phi_{3,r}(r) + … $
$ \phi_{rr}(r,p) = \phi_0,{rr}(r) + p\phi_{1,rr}(r) + p^{2}\phi_{2,rr}(r) + p^{3}\phi_{3,rr}(r) + … $
Ce qui donne : $ (1-p) [\phi_0,{rr}(r) + p\phi_{1,rr}(r) + p^{2}\phi_{2,rr}(r) + p^{3}\phi_{3,rr}(r) + …] + p[\phi_{0,rr}(r) + p\phi_{1,rr}(r) + p^{2}\phi_{2,rr}(r) + p^{3}\phi_{3,rr}(r) + … + \frac{1}{r}(\phi_{0,r}(r) + p\phi_{1,r}(r) + p^{2}\phi_{2,r}(r) + p^{3}\phi_{3,r}(r) + …) + k^{2}(\phi_0(r) + p\phi_1(r) + p^{2}\phi_2(r) + p^{3}\phi_3(r) + …)] $
Par identification, comme $ p \ne 0 $ :
- Ordre 0 :
$ \phi_{0,rr}(r)=0 $ $ \Rightarrow \phi_0(r)=Ar+B $ par intégration, avec A et B des constantes.
D’après les conditions limites, on a : $ \left\{ \begin{array}{ll} \phi_0^{r_0}=A{r_0} + B=1 \\ \phi_{0,r}^{R}=A = ik\phi^{R} \textrm{ avec } \phi^{R} = AR+B \end{array} \right. $
Donc $ A = \frac{1 - B}{r_0} $ et $ B = \frac{1-ikR}{ik} A $
Alors $ A = \frac{ik}{1 + ik(r_0 - R)} $ et $ B = \frac{1-ikR}{1 + ik(r_0 - R)} $
Donc :
$ {\color{green}\phi_{0}(r)= \frac{ik}{1 + ik(r_0 - R)} r + \frac{1-ikR}{1 + ik(r_0 - R)}} $
On résout les ordres supérieurs avec WXMAXIMA. Cependant, nous n'avons pas réussi à avoir une représentation juste de la solution par homotopie sur wxMaxima.
Discussion des résultats
Intérêt de la méthode d'homotopie
La méthode d’homotopie est efficace pour approcher l’allure d’une fonction dont on ne connaît que les conditions limites. En partant d’une solution simple à l’ordre 0 (p=0), la méthode permet de converger vers la solution finale en augmentant l’ordre auquel on approxime la solution.
Comme nous avons pu le montrer, cette méthode est pertinente pour modéliser les ondes. Combinée au modèle de Berkhoff, elle permet illustrer les phénomènes de réflexion, de réfraction et de diffraction, grâce la prise en compte de la géométrie du trait de côte.
Limites du modèle
Néanmoins, l’utilisation de modèle suppose des hypothèses simplifiant la réalité. D’un point de vue physique, de nombreux paramètres ne sont pas pris en compte. L’idée qu’un fond puisse être parfaitement plat ou en pente constante limite la complexité du modèle.
De même, certaines hypothèses mathématiques prises comme les valeurs de k et L n’illustrent pas la réalité mais ont été choisi pour que le programme sur WXMAXIMA puisse être allégé en termes de calculs. De plus, l’hypothèse de l’invariabilité des paramètres k, L ou $ \omega $ n’est sûrement pas vérifié dans un modèle réel.
Infrastructures existantes pour lutter contre l'érosion
Aujourd'hui, les principaux ouvrages pour limiter l'érosion sont les digues ou les jetées. On peut prendre l'exemple d'une digue à Marseille, sur de la plage des Prophète, particulièrement exposée au vent et à la houle. Grâce à cette installation, l'érosion sur cette plage est moins importante qu'à la Pointe rouge qui ne possède pas d'infrastructure protectrice.
- Digue de la plage des Prophètes
Conclusion
Par conséquent, le modèle utilisé présente des limites à considérer. Toutefois, il reste utile pour avoir une idée de la forme des vagues près des côtes. Aujourd’hui, la modélisation de la houle devient indispensable pour prévoir l’impact des vagues sur les littoraux. Elle constitue un outil d’aide à la décision pour choisir le type d’infrastructure à mettre en place et protéger les côtes de l’érosion.
Bibliographie
Wikipédia, Bessel function, https://en.wikipedia.org/wiki/Bessel_function
Images utilisées pour les vidéos
Diffraction : https://www.shutterstock.com/fr/search/diffraction
Shoaling :
Réfraction :
Réflexion :
 S'abonner à un flux RSS
S'abonner à un flux RSS