ANSWER - Propagation d une onde dans un estuaire a berges convergentes linéaires
Éléments de contexte
Cette fiche fait suite à la fiche "Propagation d'une onde dans un estuaire à pente du fond inclinée" mais traite de la propagation d'une onde dans un estuaire à gabarit rectangulaire dont la section se rétrécie linéairement vers l'amont et dont la pente du fond est nulle.
Modélisation mathématique du phénomène de propagation d'une onde dans un estuaire
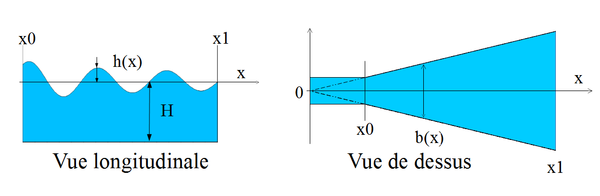
Nous prendrons en compte dans cet exemple un canal de section rectangulaire.
Hiérarchie des hypothèses simplificatrices
Les simplifications qui suivent nous permettent de développer un modèle linéaire de propagation d'une onde à l'intérieur d'un domaine à géométrie simplifiée, correspondant à un canal avec une pente de fond, qui peut se rapprocher d'un estuaire schématique à l'intérieur duquel se propage une onde de surcote.
Navier-Stokes
- → fluide incompressible
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
- → accélération négligeable
- → frottement négligeable
- → accélération négligeable
- → intégration dans une section de calcul (canal rectangulaire) ==> Saint-Venant 1D
Expression du modèle simplifié
A partir des hypothèses précédentes, considérons un canal infini de forme rectangulaire et avec pente constante : largeur $ b $, pente du fond $ S_0 $ nulle et la profondeur d'eau $ H $ constante sur l'ensemble de l'estuaire.
Soit :
- $ h(x) $ le niveau d'eau
- $ u(x) $ la vitesse moyenne de l'écoulement dans la section de surface $ A(x)=b(x)H $
- $ Q(x) $ le débit à l'abscisse $ x=A(x)u(x) $
- $ b(x)=b_0\dfrac{ x }{ x_0 } $ la largeur du canal qui varie linéairement avec l'abscisse, $ b_0 $ étant la largeur du canal à l'abscisse $ x_0 $ en amont du domaine.
Les équations qui régissent le phénomène sont les équations de Saint-Venant 1D linéarisées.
$ \begin{cases} b\dfrac{ \partial h }{ \partial t }+ \dfrac{ \partial Q }{ \partial x }=0 } \\ \\ \dfrac{ \partial Q }{ \partial t }+gA \dfrac{ \partial h }{ \partial x }=0 \end{cases} $
En dérivant la première équation par rapport au temps et la seconde par rapport à l'espace et en éliminant le terme commun, nous obtenons :
$ b\dfrac{ \partial^2 h }{ \partial t^2 }- g\dfrac { \partial A}{ \partial x } \dfrac{ \partial h }{ \partial x } -gA\dfrac{ \partial^2 h }{ \partial x^2}=0 $
nous allons supposer que $ h $ est de la forme $ h=A(x)e^{-i\sigma t} $, il vient:
$ x^2\dfrac{ \partial^2 h }{ \partial x ^2}+x\dfrac{ \partial h }{ \partial x}+k^2 x^2 h=0 $
avec :
$ k^2=\dfrac{ \sigma^2}{ gH} $
Remarque : cette équation nous montre que la répartition de la hauteur de l'onde est indépendante de la section de l'estuaire.
Solution analytique
Le schéma suivant élaboré sous Pearltrees illustre les différentes solutions analytiques dans le domaine maritime.
La solution élaborée ici en constitue une perle.
On reconnait une équation de type Bessel:
$ x^2y''+(2p+1) x y'+(\alpha^2x^{2r}+\beta^2)y=0 $
La solution de cette équation est donnée par:
$ y=x^{-p} \left[ c_{1} J_{P/r} (\alpha x^{r}/r) + c_{2} Y_{P/r} (\alpha x^{r}/r) \right] $
Les fonctions $ J_{P/r} $ et $ Y_{P/r} $ sont les fonctions de Bessel respectivement de première et de seconde espèce.
Dans notre cas, nous avons : $ p=0 , \beta=0, \alpha=k, r=1 $
avec $ P=\sqrt{p^2-\beta^2}=0 $ d'où:
$ h(x)=\left[ c_{1} J_{0} (kx)+c_{2} Y_{0} (kx) \right]e^{-i\sigma t} $
L'équation de quantité de mouvement nous permet de calculer la vitesse $ u(x,t) $
$ b\dfrac{ \partial h } { \partial t}+\dfrac{ \partial }{ \partial x} (bHu)=0<br /> $
soit:
$ bHu=i\sigma \dfrac{ b_0 } { x_0}e^{-i\sigma t} \int_{x} x \left[ c_{1} J_{0} (kx)+c_{2} Y_{0} (kx) \right]\, \mathrm dx $
d'où:
Pour calculer cette intégrale, nous utilisons la relation de récurrence suivante :
$ \dfrac{d}{dx} (x^n J_{n}(x))=x^n J_{n-1}(x) $
, de même pour $ Y_{n}(x) $
Nous obtenons :
$ u=i \dfrac{\sigma } { H} \left[ c_{1} J_{1} (kx )+c_{2} Y_{1} (kx ) \right] e^{-i\sigma t} $
Synthèse : expression de la solution analytique finale
En résumé, l'expression analytique exprimant la variation du niveau d'eau et de la vitesse moyenne en toute section du domaine sont données par les équations suivantes:
$ h(x,t)=\Re \Bigl(\left[ c_{1} J_{0} (kx)+c_{2} Y_{0} (kx) \right] e^{-i\sigma t}\Bigr) $
$ u(x,t)=\Re \Bigl( i \dfrac {\sigma}{H } } \left[ c_{1} J_{1} (kx) + c_{2} Y_{1} (kx) \right] e^{-i\sigma t}}\Bigr) $
A partir des expressions générales de $ h(x,t) $ et de $ u(x,t) $, nous pouvons déterminer la solution en fixant 2 conditions aux limites du domaine. Nous allons considérer les deux cas suivants:
- propagation d'une onde incidente à partir de l'aval (droite) vers l'amont du domaine avec condition de sortie libre à l'extrémité amont (gauche)
- réflexion de la même onde incidente à partir de l'aval (droite) vers l'amont avec condition de réflexion totale à l'extrémité amont (gauche)
Solution analytique : propagation d'une onde vers l'amont
Nous allons imposer 2 conditions limites pour déterminer les deux constantes d'intégration.
- une condition limite aval d'entrée de l'onde à l'intérieur du domaine par la droite $ h(x_1,t)=A(x_1,t) e^{-i\sigma t}=a(x_1,t)e^{(kx_1 -\sigma t)}=a(x_1,t)e^{i\phi} \quad\forall t $
- une condition limite amont de sortie de l'onde sous forme de condition de sortie libre de type Sommerfeld:
$ h(x,t)=a(x_0) e^{i\phi } $
En dérivant cette expression, nous obtenons:
$ \dfrac{ dh }{ dx }=e^{i\phi}\dfrac{ da }{ dx }+iae^{i\phi}\dfrac{ d\phi }{ d x } $
Chaque terme exprime un processus:
- prise en compte du shoaling : $ \dfrac { d a }{ d x }=- \dfrac { 1 }{ 4 } \dfrac { S_0 }{ H } a $. La pente étant nulle, le terme de shoaling s'annule.
- équation eikonale : $ \dfrac{ d\phi }{ d x }=i\lambda $
Nous obtenons:
$ \dfrac{ d h }{ d x }= iae^{i\phi}=-\lambda e^{i\phi}= -\lambda h $
soit:$ \left \dfrac{ dA }{ dx } \right|_{x_0} = -i\lambda A(x_0,t) $
$ \dfrac{dA}{dx}=k\Big(c_{1} \dfrac {d } {dx} [ J_{0} (kx ) ]+c_{2} \dfrac{d } {dx} [ Y_{0} (kx )] \Bigl) $
Or :
$ \dfrac {d } {dz} J_{0}(z) =- J_{1} (z)\quad \text{et}\quad \dfrac {d } {dz} Y_{0}(z) =- Y_{1} (z) $
Nous obtenons le système suivant :
$ \begin{cases} \beta \Bigl(c_{1} J_{1}(kx_0) +c_{2} Y_{1}(kx_0) \Bigr)+\alpha \Bigl(c_{1} J_{0}(kx}) +c_{2} Y_{0}(kx) \Bigr)=0 \\ \\ c_{1} J_{0}(kx_1) +c_{2} Y_{0}(kx_1}) =A_1 \end{cases} $
avec :
$ \alpha=-\dfrac {i\sigma} {\sqrt{gH} } $ et $ \beta=k $
Il vient :
$ \begin{cases} c_1 = \dfrac{ -A_1 (\beta Y_{1}(kx_0) + \alpha Y_{0}(kx_0 )) } { Y_{0} (kx_1 ) ( \beta J_{1}(kx_0) + \alpha J_{0}(kx_0 )) - J_{0}(kx_1) ( \beta Y_{1}(kx_0) + \alpha Y_{0}(kx_0 )) } \\ \\ c_2 = \dfrac{ A_1 (\beta J_{1}(kx_0) + \alpha J_{0}(kx_0)) } { Y_{0} (kx_1 ) ( \beta J_{1}(kx_0) + \alpha J_{0}(kx_0 )) - J_{0}(kx_1) ( \beta Y_{1}(kx_0) + \alpha Y_{0}(kx_0 )) } \end{cases} $
Finalement, le niveau d'eau est donné par :
$ h(x)=\Re\Big[ \left(c_{1} J_{0} (kx)+c_{2} Y_{0} (kx) \right)e^{-i\sigma t}\Bigr] $
Cas d'application : translation d'une onde sinusoïdale
Le cas que nous présentons met en scène l'agitation d'une portion d'estuaire soumis à une onde de marée de période de 15 minutes. La longueur considérée est de 80 km.
Les caractéristiques de cet exemple sont les suivants:
- période de la marée : 15 minutes
- amplitude : 1 m
- pente du fond : 0 m/m
- profondeur : 100 m
Solution analytique : réflexion d'une onde à l'intérieur du domaine
Introduisons les conditions limites suivantes, qui correspondent à :
- une condition limite aval d'entrée de l'onde à l'intérieur du domaine par la droite $ h(x_1,t)=A_1(x_1,t) e^{-i\sigma t}\quad\forall t $
- une condition limité amont de réflexion totale de l'onde $ u(x)=0 \quad\forall t $
Nous aboutissons au système suivant :
$ \begin{cases} c_1 J_{1}(kx_0)+c_2 Y_{1}(kx_0) =0 \\ \\ c_1 J_{0}(kx_1)+c_2 Y_{0}(kx_1) =a_0 \end{cases} $
Dont la résolution conduit à:
$ \begin{cases} c_1 = \dfrac{A_1 Y_{1}(kx_0)} { Y_{1}(kx_0) J_{0}(kx_1)-Y_{0}(kx_1) J_{1}(kx_0)} \\ \\ c_2 = \dfrac{-A_1 J_{1}(kx_0)} { Y_{1}(kx_0) J_{0}(kx_1)-Y_{0}(kx_1) J_{1}(kx_0)} \end{cases} $
Cas d'application : réflexion d'une onde sinusoïdale
Le même cas que ci-dessus est utilisé, mais en imposant les conditions limites de réflexion. Nous obtenons l'animation suivante :
Conclusions
Cette animation montre la formation de ventres et de creux réguliers ce qui représente une réflexion totale.
La longueur d'onde diminue de manière progressive vers l'amont en fonction de la hauteur d'eau. On note également une augmentation de l'amplitude des battements vers l'amont.
Ainsi, en l'absence de tout frottement, l'onde se propage sans perte d'énergie avec pour seule cause de déformation la remontée du fond (à comparer avec le cas similaire sans pente où l'on n'observe aucune déformation).
Conclusion générale sur la simulation de la propagation d'une onde dans un estuaire à pente du fond constante et à section à convergence linéaire
Une retombée intéressante de cet exemple vient de la bonne formulation de la condition de sortie de l'onde en amont des l'estuaire (condition de sortie libre) où la condition de Sommerfeld a été utilisée avec succès.
Bibliographie
- Le Méhauté B., "An Introduction to Hydrodynamics & Waterways" Springer-Verlag, 1976, 315 p.
- Thual O., "Hydrodynamique de l'environnement", Les éditions de l'Ecole Polytechnique, Oct. 2011, 314 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 1 - Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 471 p.
- Dinguemans M. W., "Water Wave Propagation Over Uneven Bottoms - Part 2 - Non-Linear Wave Propagation", Advanced Series on Ocean Engineering - Volume 13, World Scientific, 494 p.
- Tanguy J.M. "Traité d'hydraulique environnementale", vol.2, "processus maritimes", reps. publi. JM Tanguy, Ed. Hermès - Lavoisier, 2010.
- site du SHOM et plus particulièrement une page dédiée aux courants de marée
Code Scilab
Les animations précédentes ont été réalisées à l'aide le l'application SCILAB.
Elles peuvent être utilisées pour reproduire le graphique. Il suffit de sélectionner l'ensemble du texte dans le fichier *.pdf et de le copier dans l'éditeur du logiciel puis d'exécuter le programme.
Le fichier est disponible ici : Fichier:Estuaire avec correction.pdf fournit le code SCILAB du programme qui fournit les animations précédentes.
Note : d'autres personnes peuvent avoir contribué au contenu de cet article, [Consultez l'historique]. |
 S'abonner à un flux RSS
S'abonner à un flux RSS