ANSWER : modèles analytiques de propagation d'ondes dans les estuaires
Modèles analytiques hydrodynamiques pour quantifier les effets du changement climatique sur les estuaires
Sommaire |
Historique sur le développement des solutions analytiques
Le développement de l’informatique dans les années 1960 a rendu possible de nouvelles recherches en numérique et a abouti au développement d'outils de simulation maintenant largement utilisés par les chercheurs, les sociétés d'ingénierie et les gestionnaires de rivières de domaines hydrauliques.
Ces modèles numériques sont des outils très puissants, capables de donner des réponses précises aux décideurs, mais présentent certaines limites en termes de flexibilité et surtout de temps et de complexité de mise en œuvre.
La forte demande en matière d’études portant sur l’évaluation des conséquences du changement climatique en termes d’exhaussement du niveau des océans et ses conséquences sur l’inondabilité des côtes et des estuaires, rend indispensable l’utilisation d’outils très simples à mettre en œuvre, très rapides en temps calcul et précis sur de grands linéaires (estuaires) ou sur de grandes surfaces (côtes).
Les développements modernes en matière de dynamique estuarienne datent déjà de nombreuses années.
- Sir Horace Lamb [1] a posé les premiers principes de la propagation de la marée dans des canaux de caractéristiques différentes à l’aide de résolution analytique des équations de Saint-Venant 1D.
- J.N. Hunt (1963) [2] a ainsi étudié, de manière très rigoureuse, l’effet du frottement linéarisé sur la propagation de la marée dans un canal droit (i) puis dans des estuaires à convergence exponentielle (ii) et à pente linéaire doublé d’une convergence en puissance (3/2) de la distance (iii). Les conditions aux limites sont une onde incidente côté océan et soit une sortie libre, soit une réflexion totale côté rivière.
- D. Prandle (1980) [3] s’est intéressé à des estuaires avec des variations puissances de la largeur b(x)=bLxn et de profondeur h(x)=xm, prenant en compte des conditions amont soit de sortie libre soit de réflexion totale. Il montre en particulier l’effet important du frottement en termes de variation de niveau d’eau et de déphasage, retrouvant les comportements hypersynchrones et hyposynchrones des estuaires. Il met également en évidence une modification de la période naturelle.
- S. Lanzoni et Seminara (1998) [1] étudient le comportement des estuaires à convergence exponentielle, à très faible pente et à débit amont fluvial négligeable. Utilisant une résolution par la méthode de perturbation, cela les conduit à résoudre les équations linéaires et non-linéaires. Ils montrent que le type de modélisation dépend directement du rapport entre la convergence des berges et la dissipation d’énergie crée par la rugosité du fond. Ils distinguent les estuaires faiblement dissipatifs à convergence faible où il utilise la méthode des perturbations, les estuaires faiblement dissipatifs à convergence modérée ou forte, qui rendent nécessaire la prise en compte de termes non-linéaires de convection, produisant une déformation du profil temporel de l’onde avec un raccourcissement du jusant et un raidissement du flot.
- C.T. Friedrichs (2010) [4] présente de manière très didactique 9 cas d’estuaires à fond plat avec des formulations mathématiques linéarisées adaptées à leurs dynamiques propres.
- L.C. van Rijn (2011) [5] résout le système linéarisé 1D Saint-Venant pour des estuaires avec convergence et pente du fond exponentielles. Il prend en compte les effets cumulés de la convergence (due à la pente ascendante et à la convergence des berges), en opposition avec l’effet de dissipation dû à la rugosité des fonds, qu’il exprime sous forme du terme de frottement linéarisé. En fonction du poids relatif de ces processus, il identifie A : les estuaires « idéaux ou synchrones » lorsque le niveau d’eau et la vitesse restent constants, B : les estuaires « hypersynchrones » lorsque l’inertie et la convergence dominent la dissipation par frottement, C : les estuaires « hyposynchrones » lorsque la dissipation par frottement est dominent l’inertie et la convergence des berges.
Les divers auteurs mettent l’accent sur l’importance de disposer de solutions analytiques afin de disposer de modèles simples rapidement mis en œuvre pour mieux comprendre la dynamique des estuaires de formes schématiques. Ils permettent de tester les valeurs de différents paramètres, de conditions limites, de faire ressortir les déphasages, les variations de célérité, de période, de manière explicite, ce qui aide grandement à leur compréhension. Pour cela, plusieurs auteurs utilisent de nombreuses approximations dans les systèmes d’équations à résoudre, inhérentes à chaque configuration.
Notre approche consiste à rechercher des solutions mathématiques très rigoureuses qui résolvent les systèmes linéarisés complets (hors convection non-linéaire) adaptés à des configurations géométriques spécifiques (pentes, convergence des berges, rugosité) Ces nouveaux outils de simulation vont compléter et non se substituer aux outils numériques existants. Grâce à ces solutions, ils constituent d’excellents outils de pré-dimensionnement et sont tout à fait adaptés à l’évaluation des conséquences du changement climatique en termes de variation de niveau d’eau dans les estuaires.
Solutions analytiques
Nous avons travaillé à partir des équations 1D linéarisées de Saint-Venant en faisant les hypothèses suivantes :
- (i) frottement linéarisé,
- (ii) convection non linéaire négligée,
- (iii) pente du fond assez faible.
| (1) | $ \begin{cases} B\dfrac{ \partial h }{ \partial t }+\dfrac{ \partial Q }{ \partial x }=0 \\\\ \dfrac{ \partial Q }{ \partial t }+gS\dfrac{ \partial h}{ \partial x }+fQ=0 \end{cases} $ |
Les estuaires choisis se présentent sous la forme d’un canal de section rectangulaire avec un axe de symétrie, un fond plat ou pentu (pente constante), une convergence des berges soit nulle (gabarit uniforme), linéaire ou exponentielle. Les conditions limites sont les suivantes :
- Condition aval de type océanique : entrée d’une onde longue
| (2) | $ h(x_0,t)=a_0\cos(\omega t) $ |
- Condition amont de type fluvial : sortie libre d’une onde longue. Cette condition est de type Sommerfeld :
| (3) | $ \dfrac{ \partial h }{ \partial x }\Bigg|_L-ik_Lh_L=0 $ avec $ k_L=\dfrac{\omega}{\sqrt{gH_L}} $ |
Pour toutes les configurations, nous supposons que h est de la forme: $ h(x,t)=A(x)e^{-i\omega t} $
En dérivant cette expression, nous obtenons:
$ \dfrac{ \partial h }{ \partial t }=-i\omega A(x)e^{-i\omega t} $ et $ \dfrac{ \partial^2 h }{ \partial t^2 }=-\omega^2 h $
Estuaire fond plat et gabarit uniforme
La solution a été établie par d’Alembert : $ h(x,t)=a_0\cos(kx-\omega t) $
Estuaire fond plat et berges convergentes linéaires
La section d’écoulement a pour expression: $ S(x)=H_0B(x)=H_0(B_0-2p_bx) $ où H0 est la profondeur d’eau constante, B0 est la largeur de l’estuaire à l’abscisse $ x=x_0 $ , côté océan et $ p_b $ la pente de convergence des berges. En dérivant la première équation du système (1) par rapport au temps et la seconde par rapport à l’espace, nous obtenons: $ -(B_0-2p_bx)\dfrac{ \partial^2 h }{ \partial t^2 } + gH_0(B_0-2p_bx)\dfrac{ \partial^2 h }{ \partial x^2 }-gH_02p_b\dfrac{ \partial h }{ \partial x }-f(B_0-2p_bx)\dfrac{ \partial h }{ \partial t }=0 $
En posant $ X=\dfrac{ B_0 }{ 2p_b} -x $ , la relation précédente devient: $ X^2\dfrac{ \partial^2 h }{ \partial X^2 } + X\dfrac{ \partial h }{ \partial X }+k^2_fX^2h=0 $ , avec $ k^2_f=\dfrac{ \omega(\omega+if) }{ gH_0 } $ Cette équation est une équation linéaire du second ordre de type Bessel, de forme générale :
| (4) | $ X^2h_{XX}+(2m+1)Xh_X+ [(\alpha^2X^{2r})+\beta^2]h=0 $ |
qui a pour solution: $ A(X)=X^{-m}[c_1J_{m/r}(\alpha X^r/r)+c_2Y_{m/r}(\alpha X^r/r) $
Les fonctions $ J_{m/r} $ et $ Y_{m/r} $ sont les fonctions de Bessel respectivement de première et de seconde espèce. La hauteur d’eau peut ainsi s’exprimer par $ h(X)=\mathcal{R}\Big(\big[c_1J_0(k_fX)+c_2Y_0(k_fX)\big]e^{-i\omega t} \Big) $
L’introduction des conditions limites (2) et (3) fournit les valeurs des coefficients :
$ c_1=-\dfrac{a_0}{D}\Big(Y_1(k_fX_L)+i \dfrac{k_L}{k_f}Y_0(k_fX_L)\Big) $ et $ c_2=\dfrac{a_0}{D}\Big(J_1(k_fX_L)+i \dfrac{k_L}{k_f}J_0(k_fX_L)\Big) $
où
$ D=Y_0(k_fX_0)\Big[J_1(k_fX_L)+i \dfrac{k_L}{k_f}J_0(k_fX_L)\Big]-J_0(k_fX_0)\Big[Y_1(k_fX_L)+i\dfrac{k_L}{k_f}Y_0(k_fX_L)\Big] $
Ces expressions permettent de calculer $ h(X) $ puis $ h(x) $.
Estuaire pentu de section rectangulaire uniforme
La section alors pour expression $ S(x)=HB(x)=B_0(H_0-px) $ . Posons $ X=\dfrac{H_0}{p}-x $.
Nous obtenons l’équation différentielle suivante: $ X^2\dfrac{ \partial^2 h }{ \partial X^2 } + X\dfrac{ \partial h }{ \partial X }+k^2_fXh=0 $ , avec $ k^2_f=\dfrac{ \omega(\omega+if) }{ gp } $
Cette équation est une équation linéaire du second ordre de type Bessel, de forme générale (4) qui a pour solution: $ h(X,t)=\mathcal{R}\Big(\big[c_1J_0(2k_f\sqrt{X})+c_2Y_0(2k_f\sqrt{X})\big]e^{-i\omega t}\Big) $
Les fonctions $ J_{m/r} $ et $ Y_{m/r} $ sont les fonctions de Bessel respectivement de première et de seconde espèce.
L’introduction des conditions limites (2) et (3) fournit les valeurs des coefficients :
$ c_1=-\dfrac{a_0}{D}\Big(\dfrac{Y_1(2k_f\sqrt{X_L})}{\sqrt{X_L}}+i \dfrac{k_L}{k_f}Y_0(2k_f\sqrt{X_L})\Big) $ et $ c_2=\dfrac{a_0}{D}\Big(\dfrac{J_1(2k_f\sqrt{X_L}}{\sqrt{X_L}}+i \dfrac{k_L}{k_f}J_0(2k_f\sqrt{X_L})\Big) $
où
$ D=Y_0(2k_f\sqrt{X_0})\Big[\dfrac{J_1(2k_f\sqrt{X_L})}{\sqrt{X_L}}+i \dfrac{k_L}{k_f}J_0(2k_f\sqrt{X_L})\Big]-J_0(2k_f\sqrt{X_0})\Big[\dfrac{Y_1(2k_f\sqrt{X_L})}{\sqrt{X_L}}+i\dfrac{k_L}{k_f}Y_0(2k_f\sqrt{X_L})\Big] $
Ces valeurs permettent de calculer $ h(X) $ puis $ h(x) $.
Estuaire fond plat à convergence des berges exponentielle
La section d’écoulement a pour expression: $ S(x)=H(x)B(x)=HB_0e^{bx} $
En utilisant la même démarche que précédemment, nous obtenons l’équation suivante: $ \dfrac{ \partial^2 h }{ \partial x^2 } + b\dfrac{ \partial h }{ \partial x }+k^2_fh=0 $ , avec $ k^2_f=\dfrac{1}{ c^2 }\omega (\omega+fi) $ le nombre d'onde avec frottement. de type Bessel, de forme générale (4) qui a pour solution: $ h(X,t)=\mathcal{R}\Big(\big[c_1e^{\lambda_1x}+c_2e^{\lambda_2x}\big]e^{-i\omega t}\Big) $
avec $ \lambda_i=\dfrac{-b \pm \sqrt{b^2-4k^2_f}}{2},i=1,2 $
En appliquant les conditions limites précédentes (2) et (3), nous obtenons les coefficients suivants:
$ c_1=a_0/\Big[1-\dfrac{\lambda_1-ik_0}{\lambda_2-ik_0}\Big]e^{(\lambda_1-\lambda_2)} $ et $ c_2=a_0-c_1 $
ce qui nous permet de calculer $ h(X) $ puis $ h(x) $ .
Estuaire fond pentu et à convergence des berges exponentielle
La section d’écoulement a pour expression: $ S(x)=H(x)B(x)=pxB_0e^{bx} $
En utilisant la même démarche que précédemment, nous obtenons l’équation suivante: $ x\dfrac{ \partial^2 h }{ \partial x^2 } + (1+bx)\dfrac{ \partial h }{ \partial x }+k^2_fh=0 $ , avec $ k^2_f=\dfrac{1}{ gp }\omega (\omega+fi) $ le nombre d'onde avec frottement.
Cette équation différentielle linéaire du second ordre est de type Kummer qui a pour solution:
$ h(x,t)=\mathfrak{R} \bigg[ \dfrac{e^{-bx/2}}{\sqrt{x}} \Big(c_1 WhittakerM \Big[ \dfrac{2k^2_f-b}{2b};0;bx \Big] +c_2 WhittakerW \Big[ \dfrac{2k^2_f-b}{2b};0;bx \Big] \Big)e^{-i\omega t} \bigg] $
où WhittakerM et WhittakerW sont les fonctions de Whittaker, qui font partie de l’arsenal des fonctions Confluentes Hypergéométriques. Les coefficients c1 et c2 sont déterminés par les conditions limites. Les calculs ont été réalisés avec le logiciel de calcul formel Maple.
Nous présentons ici un exemple de propagation d’une onde dans un estuaire schématique sans rugosité, avec les valeurs numériques suivantes: longueur du canal: 50m, Cas 1 : profondeur 10 m, période 10s, amplitude de l’onde amont : 0.2m Cas 2 : pente du fond 4%, profondeur 20 m, période 15s, amplitude amont : 0.5m Les 2 courbes correspondent à la superposition de la solution analytique avec les résultats obtenus avec TELEMAC 2D.
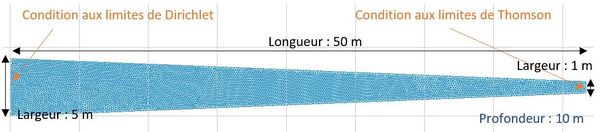 |
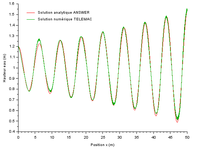
|
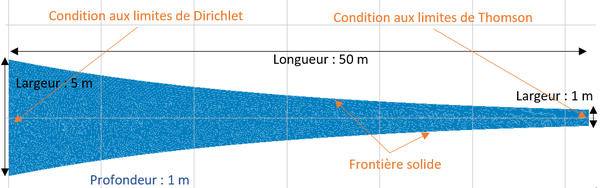 |

|
(les simulations avec TELEMAC ont été réalisées par Marine Deniau étudiante ENTPE 2A).
Il est à remarquer que la durée d’exécution de ces calculs n’est que de quelques secondes qui permet de disposer de la valeur de la variation du niveau d’eau en tout temps en tout point de l’estuaire.
Bibliographie
- Sir Lamb H., (1945), « Hydrodynamics », Dover publications, 768 p.
- Hunt J.N., 1964, « Tidal Oscillations in Estuaries », Geophysical Journal of the Royal Astronomical Society, 8, 440-455.
- Prandle D., Rahman M., 1980, « Tidal Response in Estuaries », Journal of Physical Oceanography, Vol.10, 1552-1573.
- Lanzoni S., Seminara G., 1998, « On tide propagation in convergent estuaries », Journal of Geographycal Research, Vol. 103, NO. C13, Pages 30-793-30,812.
- Friedrichs C.T., 2010, « Barotropic tides in channelized estuairies », Issues in Estuaries Physics, Cambridge University Press, Cambridge UK, 2010.
- Van Rijn L.C., « Analytical and numerical analysis of tides and salinities in estuaires ; part 1 : tidal wave propagation in convergent estuairies, Ocean Dynamics (2011) 61 :1719-1741.
Auteurs
Jean-Michel Tanguy1 , Hassan Smaoui2,3
- Hydrologik, 7, rue des Halles 44210 Pornic – jm.tanguy@shf-hydro.org
- CEREMA, 134 Rue de Beauvais, 60280 Margny-lès-Compiègne - hassan.smaoui@cerema.fr
- Sorbonne Université, UTC, Laboratoire Roberval/LHN, FRE-CNRS 2012, CS 60319, 60203 Compiègne
- Proposed topic: Adaptation des estuaires et des zones humides
- Key words: changement climatique, submersion, inondations, outils temps réel, Climate change, estuary, flooding, real time modeling
 S'abonner à un flux RSS
S'abonner à un flux RSS
