B.03 - Estimation d'une pluie de bassin par interpolation de postes pluviométriques
Sommaire |
Contexte
Les postes pluviométriques au sol fournissent des observations ponctuelles des pluies (fiche B.02). Nous avons besoin de connaître la lame d'eau précipitée sur le bassin : il est donc nécessaire d'estimer la pluie en tout point à partir d'un (petit) nombre d'observations ponctuelles. Différentes méthodes d'interpolation sont utilisées ; cette opération introduit une incertitude sur la lame d'eau précipitée.
Description des différentes méthodes
Méthodes d'interpolation déterministes
Elles consistent en une moyenne pondérée des observations telle que les facteurs de pondération reposent sur des propriétés géométriques du réseau de pluviomètres, sans tenir compte du phénomène physique : ![]() .
.
où Pi désigne la pluie ponctuelle observée au ie poste et αi est le facteur de pondération associé.
La méthode la plus triviale est la moyenne arithmétique simple, avec la même pondération pour toutes les observations. La méthode des polygones de Thiessen est un peu plus élaborée. Elle définit la zone d'influence de chaque pluviomètre comme étant l'ensemble des points au sein du bassin étudié, qui ont pour plus proche station, ce pluviomètre (Fig. 1). Le facteur de pondération de ce dernier est alors proportionnel à l'aire Ai de ce bassin[1] : 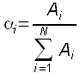 .
.
Méthodes d'interpolation probabilistes
Elles font appel à des modèles probabilistes du champ précipitant et découlent de l’analyse statistique des données pluviométriques. Ces méthodes s'inspirent fortement des techniques géostatistiques.
Le krigeage est considéré comme étant l’une des méthodes les plus performantes. Elle estime la pluviométrie en tout point du bassin par une combinaison linéaire pondérée des observations. La pondération repose sur l'auto-corrélation spatiale du champ précipitant décrite par son variogramme[2] : le krigeage débute par la construction du variogramme du champ précipitant (basé sur l’analyse du variogramme expérimental des observations disponibles et des hypothèses sur le champ pluvieux (souvent modélisé à l’aide d’une fonction standard, exponentielle par exemple[3]). Le variogramme est ensuite utilisé pour calculer les facteurs de pondération en tout point du bassin. Il s'agit de déterminer la combinaison de ces facteurs qui minimise la variance d'estimation, sous la contrainte que la somme des facteurs vaut 1.
Le critère de précision de l'estimation se traduit par une minimisation de l’erreur quadratique moyenne.
Avantage et limite de chacune des méthodes
Moyenne arithmétique simple
Cette méthode est assez grossière et est potentiellement source d'erreurs importantes. Elle est donc à proscrire le plus souvent. Elle reste néanmoins acceptable dans les cas suivants :
- densité importante et répartition régulière des points de mesure ;
- altitude du bassin homogène ;
- mesures ponctuelles peu différentes de la valeur moyenne (pluies stratiformes).
Polygones de Thiessen
Cette approche présente un risque d'erreur importante, car elle ne prend pas compte la structure du champ précipitant (non prise en compte de l'effet du relief ni des caractéristiques des précipitations (front, cellules convectives). Elle est à proscrire sur des bassins avec relief accentué et peu instrumenté aux altitudes les plus élevées.
Krigeage
Comparaison de la maille d’un réseau de pluviomètres aux dimensions caractéristiques d’une structure précipitante
Les incertitudes sur une lame d’eau de bassin liées à l’interpolation d’un nombre limité de mesures ponctuelles peuvent être estimées qualitativement en comparant la maille des réseaux de pluviomètres dont nous disposons (inverse de leur densité) et les dimensions caractéristiques des structures précipitantes (hétérogénéité spatiale des pluies). Les chiffres qui suivent proviennent de différentes études rassemblées par Lobligeois (2014). Leur interprétation doit tenir compte de la variabilité naturelle : il ne s’agit que d’ordres de grandeur.
Les précipitations stratiformes (fiche B.01) sont plutôt associées à l’échelle synoptique en météorologie (fronts chauds et froids...). Ces structures peuvent présenter des longueurs de plusieurs centaines de km et des largeurs de plusieurs dizaines. Elles se déplacent usuellement à des vitesses suffisamment faibles pour que l’interpolation des mesures au sol (aux pas de temps courants) capture bien le signal de pluie.
Pour des structures convectives (fiche B.01), les distances de décorrélation[6] (qu’on peut assimiler à une dimension caractéristique des structures) varient de quelques km à une vingtaine de km. Dans son mémoire sur la Loire amont, Moulin (2007) a caractérisé les champs précipitants par krigeage des mesures au sol : la portée des variogrammes était également de l’ordre de 25 km au pas de temps horaire. L’incertitude liée à l’interpolation par nos réseaux de pluviomètre est donc très importante : l’observation par les pluviomètres est souvent insuffisante[7] du fait de l’hétérogénéité spatiale des pluies.
Exemple 1. Les cumuls observés (au radar) à l'origine de la crue catastrophique de la Nivelle en mai 2007 sont représentés en figure 2. Alors que la côte basque a reçu des cumuls inférieurs à 2 mm en 4 h, on observait plus de 200 mm pendant la même période sur une partie du bassin versant de la Nivelle distante d'une dizaine de kilomètres seulement.
Exemple 2. Le SPC Seine moyenne – Yonne – Loing (DRIEE d’Île-de-France) a mené une étude sur l’estimation de pluie de bassin basée sur les données d’un réseau d’environ 100 pluviomètres au sol (dont 94 postes horaires, les autres fonctionnant au pas de temps journalier) situés principalement sur les bassins de l’Yonne (nord Morvan, relief marqué sur la partie amont de 200 à 800 m, plaines en partie aval de 50 à 200 m), du Loing (faible relief de 50 à 400 m, départements de l’Yonne et du Loiret) et de l’Est de l’Île-de-France (les Morins et l’Yerres, dans les départements de la Marne et de Seine et Marne). La majorité des pluviomètres (80 %) appartient au réseau Météo-France. L’étude visait à caractériser et comparer les données disponibles du réseau sol (annexe). Elle a permis de montrer que la distance moyenne inter-poste correspondant à un coefficient de corrélation (R2) entre les séries d’observations ponctuelles étaient limitées : 22 km pour R2 = 0,5 et moins de 10 km pour R2 = 0,8 (valeur pour laquelle la dispersion des points reste significative). Ces distances sont à comparer à la distance moyenne entre deux postes du réseau...
De plus, l’incertitude de la mesure des cumuls de pluie (au sol) est corrélée positivement avec l’intensité des précipitations et la force du vent. Comme les pluies convectives sont par essence intenses et souvent associées à des bourrasques, on comprend que l'estimation des cumuls significatifs pour l'hydrologie est plus délicate pour les pluies convectives que pour les pluies stratiformes[8] (fiche B.01).
Annexe
Description de l’étude du réseau pluviométrique utilisé par le SPC Seine moyenne – Yonne – Loing
L’étude présentée dans l’exemple 2 a comporté :
- la caractérisation des chroniques (scores sur les lacunes, les intensités moyennes, les occurrences de pluie...) afin de repérer certains postes particuliers (par exemple ceux présentant des lacunes récurrentes) ;
- la réalisation d’ajustements statistiques sur les chroniques horaires et du calcul des cumuls glissants sur différentes durées afin de produire des graphes Intensité-Durée-Fréquence et des cartes krigées de périodes de retour ;
- le calcul d’un indice de variabilité spatiale (cf. la thèse de Julien Lerat) défini comme étant le rapport entre la pluie enregistrée par un poste et la pluie de bassin calculée sur les polygones de Thiessen. Même si cet indice était plus fort sur les bassins amont de l’Yonne, traduisant un écart plus important entre les mesures ponctuelles et les lames d’eau de bassin, donc une plus grande variabilité spatiale sur ces zones, les résultats obtenus sont un peu dispersés, ce qui empêche de tirer des conclusions claires ;
- le calcul de doubles cumuls, de cumuls de résidus et de la persistance pluviométrique sur les pluies journalières pour mettre en évidence des périodes « douteuses » poste par poste :
- la construction d’une base d’événements pluvieux (sélectionnés « en négatif », en caractérisant la période de temps sec qui les sépare) ;
- l’étude de la corrélation inter-postes à partir de ces bases d’événements (environ 80 événements par an pour une chronique d’une quinzaine d’années).
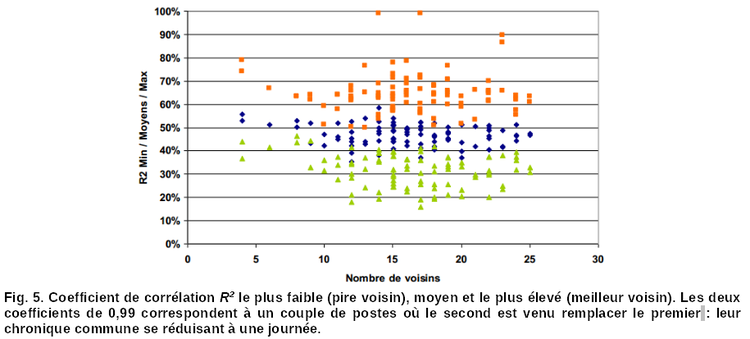
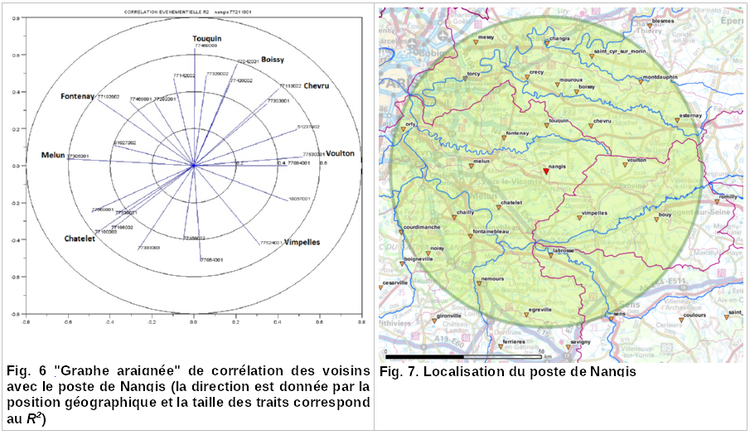
Les corrélations (menées de manière systématique dans un rayon de 50 km) sont mauvaises, avec des coefficients de corrélation R2 qui atteignent rarement 0,9. Un tel R2 de 0,9 n’a été obtenu que dans un cas : 2 postes très proches (moins d’1 km de distance, Fig. 3 à 5) avec peu de relief (Loiret). Donc, même dans ces conditions, des disparités existent. En moyenne, la corrélation au « meilleur voisin » est d’environ 0,6 – 0,7, ce qui reste assez médiocre.
À partir de ces corrélations, on a pu réaliser des graphes permettant de synthétiser la corrélation d’un poste avec ses voisins (« graphes araignées », fig. 6 et 7).
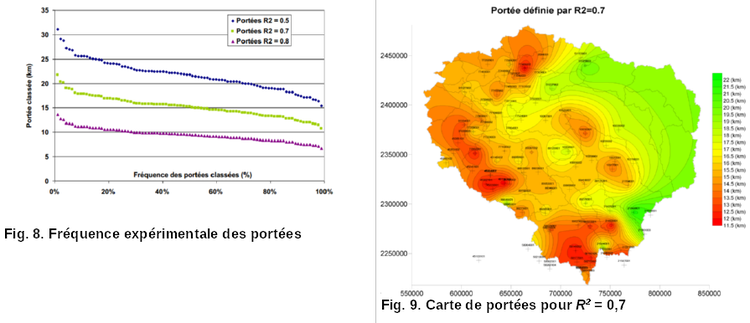
L’étude des corrélations permet ensuite de calculer des portées. En théorie, plus on s’éloigne du poste central, plus les corrélations décroissent. Une loi statistique (ici exponentielle) a été ajustée entre le coefficient de corrélation R2 et la distance au poste voisin. On en déduit la « portée » (en km) correspondant à des coefficients de corrélation fixés (ici 0,5 et 0,7). Ces informations sont ensuite représentées cartographiquement par krigeage (Fig. 9). Les cartes de portée pour des R2 de 0,5 (soit des postes qui n’ont
en pratique opérationnelle pas grand chose à voir !) et 0,7 (dans ce dernier cas, le comportement des postes est nettement différent) montrent que pour le secteur de l’Yonne amont, la portée pour R2 = 0,7 est inférieure de l’ordre de 12 km, sur le Loing amont de l’ordre de 15 km. Autrement dit, pour avoir un coefficient de R2 de 0,7, il faudrait que les postes soient en moyenne distants de 12 à 15 km.
L’un des objectifs de ces corrélations était de voir dans quelle mesure, en opérationnel, il était pertinent de remplacer un poste défaillant par l’un de ces voisins. On peut donc retenir que les corrélations s’effondrent rapidement avec la distance et que même une corrélation de 0,7 reste médiocre en termes de dispersion des points.
Cette étude aura aussi permis d’insister sur l’insuffisance du maillage du réseau temps réel actuel pour bien appréhender tous les événements.
Voir également
Fiche B.01 – Précipitations stratiformes et convectives
Fiche B.02 – Observation ponctuelle de pluie au sol
Fiche B.04 – Estimation d'une pluie de bassin par observation RADAR
Pour aller plus loin
Bosser, P. (2011). Interpolation spatiale. Cours de l’École nationale des Sciences géographiques, département Positionnement Terrestre et Spatial.
DRIIE – SPC SmYL (2012). Analyse et comparaison des lames d’eau radar et issues d’un réseau de mesures pluviométrique au sol pour la DRIEE-SPC SMYL. Tranche A – Rapport de tranche ferme (Safège) http://extranet.schapi.i2/spip/spip.php?article1190
Lobligeois F. (2014). Mieux connaître la distribution spatiale des pluies améliore-t-il la modélisation des crues ? Diagnostic sur 181 bassins versants français. Thèse de doctorat, AgroParisTech (IRSTEA)
Musy, A., Higy, C. (2004). Hydrologie: une science de la nature. 315 p. ISBN 2-88074-546-2
Moulin L. (2007). Prévision des crues rapides avec des modèles hydrologiques globaux. Applications aux bassins opérationnels de la Loire supérieure : évaluation des modélisations, prise en compte des incertitudes sur les précipitations moyennes spatiales et utilisation de prévisions météorologiques. Thèse de doctorat, CEREVE.
http://www.ohmcv.fr/P205_critique.php?
http://www.cwc.gov.in/main/HP/download/11%20How%20to%20compile%20rainfall%20data.pdf
- ↑ La somme des aires Ai étant égale à l'aire du bassin sur lequel on souhaite estimer la pluie de bassin.
- ↑ Un variogramme est défini comme la demi-espérance des carrés des différences entre les valeurs de pluie observées aux différents postes pluviométriques, en fonction de leur interdistance.
- ↑ Pour réaliser un bon krigeage, il faudrait tenir compte de toutes les variables explicatives structurant le champ des précipitations (altitude, orientation des versants par rapport aux vents dominants etc...). C’est assez lourd ; il est souvent procédé à un krigeage simple ne prenant pas en compte ces effets. Un exemple de krigeage plus complet a été mené par Météo-France dans le cadre de la méthode Aurhély.
- ↑ Sous réserve que toutes les hypothèses sous-jacentes soient justifiées...
- ↑ D'où l'intérêt de la méthode Antilope de Météo-France (fiche B.04).
- ↑ Les distances de décorrélation indiquées dépendent d’un temps caractéristique (le temps de décorrélation ou plus simplement le pas de temps). Ici, les plus petites structures convectives sont caractérisées sur quelques minutes et les plus grandes à quelques heures.
- ↑ Des écarts considérables peuvent être constatés entre l’estimation de la pluie de bassin basée sur les observations au sol et l’estimation radar (fiche B.04, exemple sur le bassin de la Loire, tableau 1).
- ↑ On passe ici sous silence les incertitudes de l'observation en zone de montagne, car les lacunes du réseau radar et pluviométriques dans ces secteurs ou bien l'incertitude liée à la discrimination pluie/neige en altitude concerne aussi bien les deux types de pluies dont cette fiche fait l'objet. À titre d'information on peut atteindre – 50 % en mesure de neige par vent fort (cf. intervention DSO aux Journées de Crues Soudaines – janvier 2013).
 S'abonner à un flux RSS
S'abonner à un flux RSS