C.05 - Approches stochastiques (méthodes de Monte-Carlo)
Sommaire |
Principe
Pour estimer l'incertitude de prévision due à une ou plusieurs sources d'incertitude, une approche a priori simple consiste à « propager » ces incertitudes à travers le modèle. Les approches stochastiques visent à réaliser cette opération en utilisant une quantification appropriée des incertitudes sources.
La quantification des incertitudes « sources » peut prendre différentes formes. L'expression la plus complète est sans doute la densité de probabilité (fiche A.08). Cependant, la plupart des outils et modèles de prévision sont trop complexes pour que la propagation des incertitudes « sources » puisse faire l'objet d'une expression analytique (sous forme d'équations, aussi complexes soient-elles) si ces incertitudes sont décrites sous forme de densité de probabilité[1]. Les approches stochastiques contournent cette difficulté en « tirant » un nombre élevé (suffisant) de scénarios pour chaque source d'incertitude conformément à sa densité de probabilité[2].
Chaque tirage est ensuite utilisé pour une exécution du modèle. La distribution des sorties du modèle donne une description de l'incertitude de prévision. En un sens, il s'agit d'une approche multi-scénario avec un nombre de scénarios suffisants et choisis pour décrire quantitativement les sources d'incertitude.
Ses principales étapes sont :
- identification (choix) des sources d'incertitude à prendre en compte,
- quantification de ces incertitudes sources sous la forme de densités de probabilité,
- tirage numérique dans ces densités de probabilité jointes pour obtenir N « scénarios »,
- exécution du modèle sur ces N tirages,
- analyse de la distribution des sorties du modèle.
Quantification de l'incertitude et tirage
Dans un premier temps, les sources d'incertitude doivent être décrites et quantifiées. Concrètement, cette quantification peut prendre la forme d'une densité de probabilité plus ou moins précise (exemple 1).
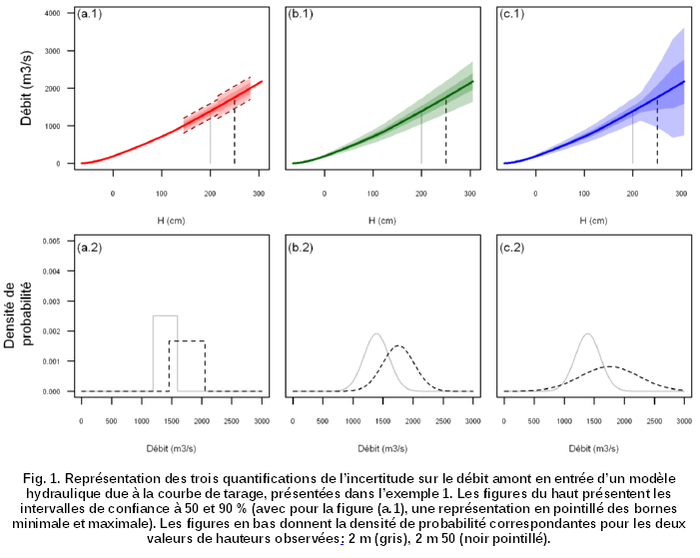
Exemple 1. Selon le degré de connaissance de la source d'incertitude, sa quantification sera plus ou moins précise. Considérons l'incertitude sur un débit, due à la courbe de tarage. La hauteur est de 2 m le 30 février (gris) puis de 2 m 50 le 31 février (noir pointillé). Différentes descriptions quantitatives de l'incertitude sur ce débit liée à la courbe de tarage sont possibles (Fig. 1) :
- a. Si on a peu d'information, on caractérisera l'incertitude seulement par un intervalle « min / max » : le débit est égal à QCT, valeur donnée par la courbe de tarage, ± 200 m3/s pour un débit entre 1 000 et 1 500 m3/s, puis ± 300 m3/s pour un débit entre 1 500 et 2 000 m3/s. Cela revient à considérer une densité de probabilité uniforme sur l'intervalle compris entre QCT – 200 et QCT + 200 m3/s (respectivement QCT – 300 et QCT + 300 m3/s).
- b. Mais on sait que les valeurs autour de la valeur centrale (donnée par la courbe de tarage) sont plus plausibles que celles proches aux bornes de cet intervalle. On peut donc opter pour une quantification de l'incertitude par une densité de probabilité issue d'une famille connue, par exemple une loi normale (gaussienne) de moyenne le débit établi par la courbe de tarage à partir de l'observation de hauteur et d'écart-type 0,15 × QCT.
- c. Comme l'incertitude augmente fortement en extrapolation (fiche B.08), on peut également choisir un écart-type de 0,40 × QCT au-delà de 2 000 m3/s (zone d'extrapolation de la courbe de tarage) avec une zone de transition pour QCT compris entre 1 500 et 2 000 m3/s.
Tirage dans la distribution et propagation
Il est possible de tirer aléatoirement des valeurs dans une densité de probabilité : plus une valeur est probable, plus sa fréquence de tirage sera élevée. De nombreux outils informatiques[3] proposent des méthodes pour tirer dans des densités de probabilité « classiques ». Il est également possible de tirer des valeurs aléatoires dans des densités plus complexes en utilisant un algorithme simple, appelé algorithme du rejet.
L'enjeu est ici de tirer aléatoirement un nombre suffisant de valeurs dans la densité de probabilité des sources d'incertitude pour que l'histogramme des valeurs tirées soient une bonne approximation de la densité de probabilité choisie pour quantifier la source d'incertitude (exemple 2).
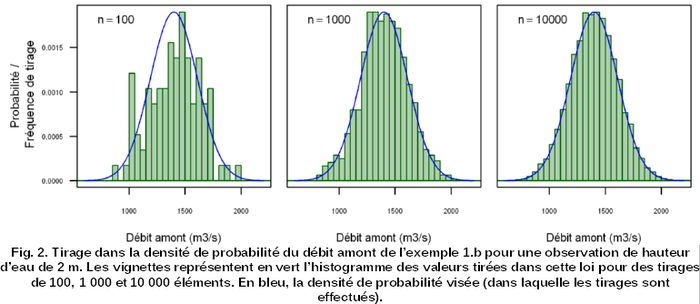
Exemple 2. Reprenons l'exemple précédent et considérons la densité de probabilité utilisée dans le cas (b) pour décrire l'incertitude (due à la courbe de tarage) sur le débit correspondant à une observation de hauteur de 2 m (Fig 1.(b.2)). Il s'agit d'une densité de probabilité normale de moyenne QCT = 1 390 m3/s et d'écart-type 0,15 × QCT. Un trop petit nombre de tirages dans cette loi de probabilité conduira à une mauvaise description numérique de cette quantification de l'incertitude source, tandis qu'un nombre supérieur sera suffisant (Fig. 2).
Une fois toutes les sources d'incertitude décrites par des tirages (en nombre suffisant), il suffit de combiner ces tirages (si on s'intéresse à plusieurs sources d'incertitude) et à exécuter le modèle avec ces valeurs. On obtiendra n1 × n2 × … × nm prévisions (avec m sources d'incertitude). L'analyse statistique de la variabilité de cet ensemble de prévisions fournit directement une quantification de l'incertitude de prévision[4] (exemple 3).
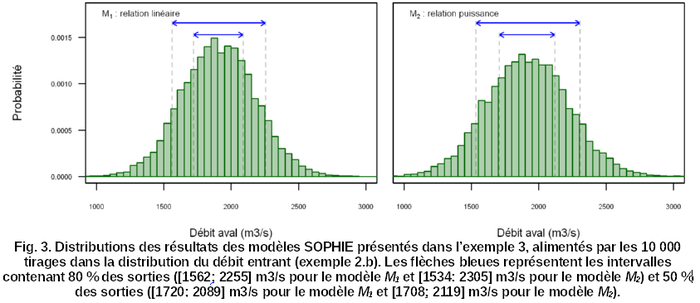
Exemple 3. Le débit présenté dans les exemples 1 et 2 est l'entrée amont de deux modèles simple « de propagation » implémentés dans la plate-forme SOPHIE. Le premier est une relation linéaire simple[5] et le second une relation Puissance : ![]() Le débit entrant est estimé grâce à la courbe de tarage à 1 390 m3/s. L'incertitude sur le débit sortant due à l'incertitude sur le débit entrant est estimée en alimentant chaque modèle avec les 10 000 tirages effectués dans l'exemple 2. Les résultats des deux modèles présentent des moyennes très proches (1 907 et 1 918 m3/s) mais les résultats du modèle M2 sont plus dispersés (écart-type supérieur) et surtout légèrement asymétrique avec un décalage vers les plus fortes valeurs (Fig. 3).
Le débit entrant est estimé grâce à la courbe de tarage à 1 390 m3/s. L'incertitude sur le débit sortant due à l'incertitude sur le débit entrant est estimée en alimentant chaque modèle avec les 10 000 tirages effectués dans l'exemple 2. Les résultats des deux modèles présentent des moyennes très proches (1 907 et 1 918 m3/s) mais les résultats du modèle M2 sont plus dispersés (écart-type supérieur) et surtout légèrement asymétrique avec un décalage vers les plus fortes valeurs (Fig. 3).
Points sensibles
Il est important de disposer d'un nombre suffisant de tirages pour avoir une bonne description de l'incertitude de chaque source (cf. exemple 2), ce qui peut conduire en pratique à devoir effectuer un très grand nombre d'exécutions du modèle : un équilibre est parfois à trouver entre qualité de la description des sources d'incertitude et mise en pratique opérationnelle (temps de calcul compatible avec la chaîne de production des prévisions en temps réel).
De nombreux modèles hydrauliques et hydrologiques sont non linéaires : certaines sources d'incertitude peuvent être réduites ou au contraire amplifiées par le modèle (fiche A.03), c'est-à-dire que l'incertitude de prévision résultante peut être très peu (respectivement, fortement) fonction de ces sources. Une analyse de sensibilité peut être utile pour déterminer les sources qu'il n'est pas nécessaire de décrire très précisément (tirage en nombre limité) ou qu'il faut au contraire décrire avec beaucoup de soin.
Des interactions entre sources d'incertitude peuvent également apparaître et certains tirages sont tout simplement inutiles. Une analyse préalable du modèle peut améliorer la stratégie de description des sources d'incertitude.
Voir également
Fiche A.03 – Propagation des incertitudes : amplification et réduction
Pour aller plus loin
Nicole Goutal (2011). Prise en compte des incertitudes dans les modèles hydrauliques_N.Goutal_EDF. Présentation aux ateliers Modélisation des 4 et 5 octobre 2012. http://extranet.schapi.i2/spip/spip.php?article937
- ↑ La propagation de ces incertitudes peut être vue comme l'interaction entre les équations du modèle (description du système) et les équations décrivant les sources d'incertitude (ici sous la forme de densités de probabilité) : le système résultant n'a souvent pas de solution analytique.
- ↑ C'est-à-dire si une source d'incertitude est la variable X et que cette variable a 10 fois plus de chances d'être égale à x1 qu'à x2, alors sur le grand nombre de tirages à effectuer, il faudra que la valeur x1 apparaisse 10 fois plus souvent que x2.
- ↑ Par exemple, le logiciel libre R (disponible sur http://cran.r-project.org/).
- ↑ Par exemple, une description statistique : moyenne, écart-type, quantiles, intervalle de prévision...
- ↑ La transformation d'une distribution normale par une relation linéaire est un des cas solubles analytiquement et l'approche stochastique n'est pas nécessaire ici... (mais valide néanmoins).
 S'abonner à un flux RSS
S'abonner à un flux RSS