Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/APPAIX MOREL SANFRANCISCO
Sommaire |
Cas n°1
Dans le premier cas, on s'intéresse à un domaine monodimensionnel plat de longueur L avec des conditions aux limites suivantes : la condition de flux aval est Φ=1 et la condition de flux en amont est Φ_x=ikΦ.
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ(x)=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 et x = L : $ Φ(x)=1 $ et $ \frac{∂Φ(x)}{∂x}=ikΦ $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ikΦ(0)=ik=-ikA+ikB $
$ \Leftrightarrow\ A+B=1 $ et $ B-A=1 $ donc $ A=0 $ et $ B=1 $
Donc la solution analytique est $ \boxed{Φ(x)=e^{ikx}} $
Homotopie
La méthode semi-analytique
La méthode semi-analytique consiste à résoudre l'équation suivante:
$ (1-p)[L(U(x,t);p)-L(u_0(x,t))] + cҢ(p)[L(U(x,t);p)-N(U(x,t);p)-f(x)]=0 $
Avec L un opérateur linéaire, N un opérateur non linéaire et f les termes complémentaires de l'équation.
Ici afin de résoudre de manière semi-analytique l'équation, il est nécessaire de coder la démarche de l'homotopie.
1) Généralisez la formule de l'homotopie
D'après la formule, on obtient :
$ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
2) poser une estimation pour u_0
En première estimation on pose $ u_0=0 $
$ (1-p)Φ_{xx}+p(Φ_{xx}+k^2Φ)=0 $ et $ Φ_{xx}+k^2Φ=0 $ car H est constant dans le premier cas
3) Développer l'expression obtenue pour différents ordres de p
Pour l'ordre 0 :
$ Φ_{0,xx}(x)-pΦ_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0 $
$ \LeftrightarrowΦ_{0,xx}(x)+pk^2Φ_0(x)=0 $ cette égalité est vraie pour tout p, donc en particulier pour p=0 donc :
$ Φ_{0,xx}(x)=0 $
En intégrant deux fois, on obtient :
$ \int_0^L Φ_{0,xx}(x)dx = Ax + B $, avec A et B deux constantes à déterminer
Or le sujet nous dit qu'à l'ordre 0, les conditions aux limites sont:
1) en x=0, $ Φ=1 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=A $
et $ Φx(x=L)=ikΦ(x=L)=ik(AL) $
donc $ A=ik(AL) $
D'où $ A=\frac{ik}{1-ikL} $;
Et on obtient $ Φ0(x)=Ax=\frac{ik}{1-ikL}*x $
Pour passer aux différents ordres, il suffira de réaliser une récurrence en faisant comme dans l'ordre 1 c'est-à-dire résoudre:
$ Φ1+k²∫∫Φ0+A2*x+B2=0 $ ( ce qui donne à l'ordre n : $ Φn+k²∫∫Φ(n-1)+A'*x+B'=0 $ )
On injecte dans l'équation ci-dessus l'expression de Φ0 trouvée précédemment.
On a alors:
$ Φ1+k²([\frac{ik}{1-ikL}]\frac{x³}{3})+A2*x+B2=0 $
Or le sujet nous dit qu'à partir de l'ordre 1, les conditions aux limites sont:
1) en x=0, $ Φ=0 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=-k²([\frac{ik}{1-ikL}]L²/2]-A2 $
et $ Φx(x=L)=ikΦ(x=L)=-ik(-k²([ik/(1-ikL)]\frac{L³}{3})+A2*L) $
donc, par identification et en généralisant, on peut dire que $ A2=[\frac{ikΦxx - Φx}{1-ikL}]L²/2] $
4) En utilisant la formule obtenue pour A, rentrer la récurrence déduite
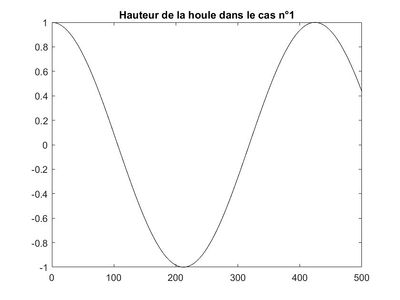
Représentation pour le cas n°1
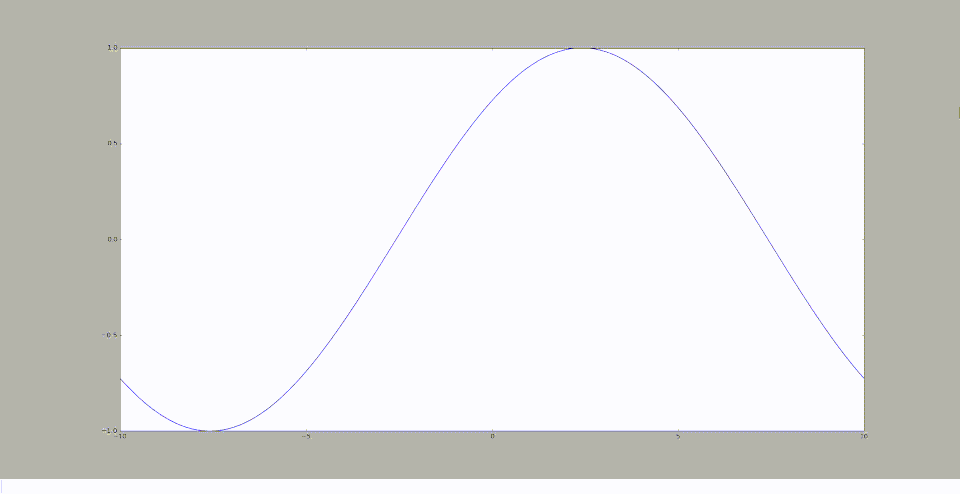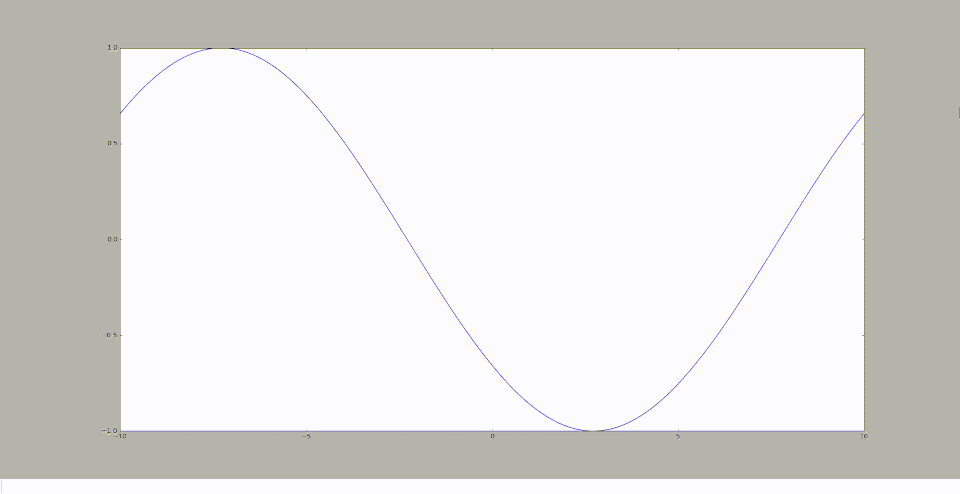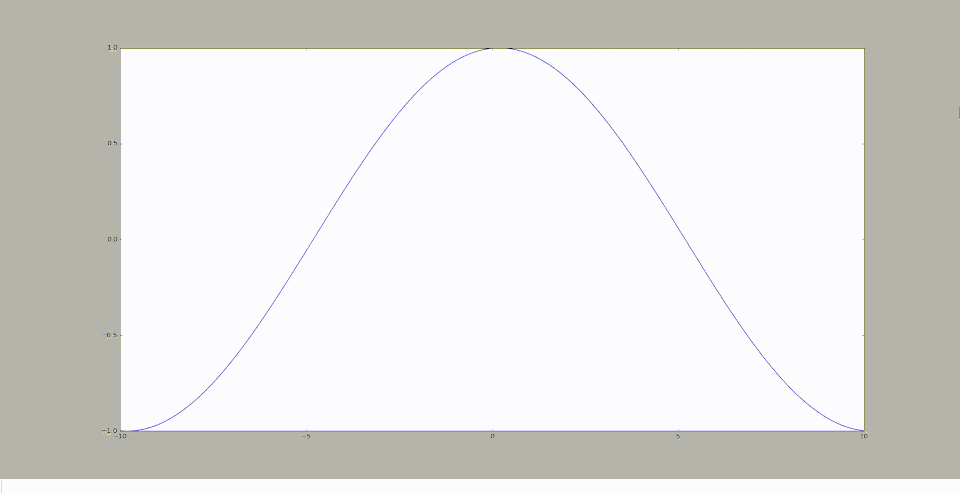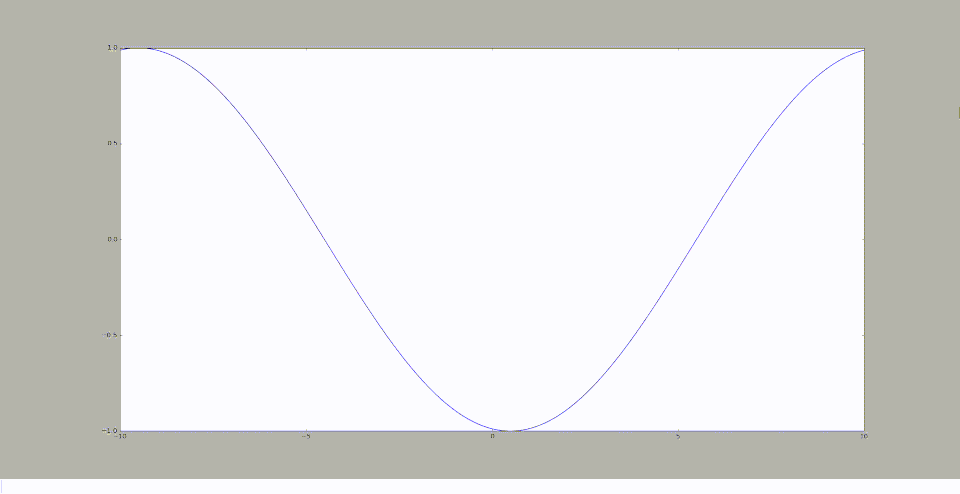
On obtient à l'aide de la méthode donnée ci-dessus codée sur Maxima, le graphique suivant:
Homotopie pour le cas avec p=20
Etude de la sensibilité du cas n°1
En testant pour différentes valeurs de nombre d'onde, notée k, nous avons observé les graphiques suivants:
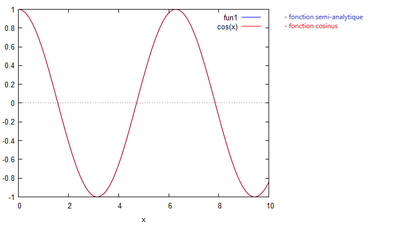
 k=0,001
k=0,001
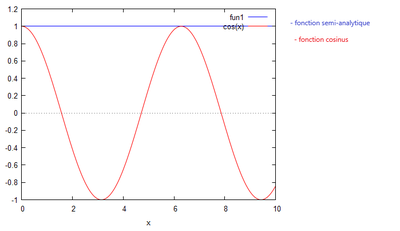
 k=1
k=1
De cette observation, nous pouvons en déduire que plus k diminue, plus la courbe se rapproche d'une droite de pente nulle
Cas n°2
Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0.
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 : $ \frac{∂Φ(x)}{∂x}=ik(2-Φ) $
en x = L : $ \frac{∂Φ(x)}{∂x}=0 $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ik(2-Φ(0))=ik $
On trouve donc $ A=\frac{e^{ikL}}{2cos(kL)} $ et $ B=1-\frac{e^{ikL}}{2cos(kL)} $
Donc la solution analytique est $ \boxed{Φ=\frac{e^{ikL}}{2cos(kL)}e^{-ikx}+(1-\frac{e^{ikL}}{2cos(kL)})e^{ikx}} $
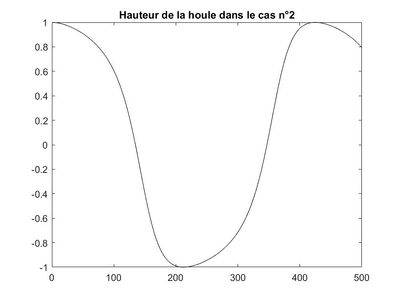
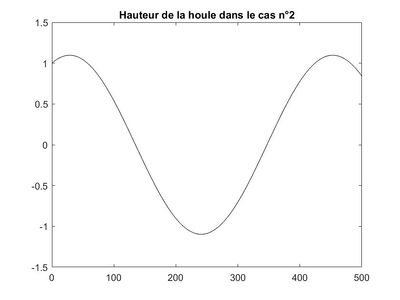
Nous avons tracé deux graphiques modélisant la hauteur de houle, celui de gauche correspond à $ H(x)=\mathbb{R}(Φ(x)/|Φ(x)|) $ et celui de droite à $ H(x)=\mathbb{R}(Φ(x)) $. On remarque que le résultat obtenu par homotopie est relativement proche de la courbe de gauche alors que celle de droite correspond bien à l'évolution de la hauteur de houle au cours du temps. Cela est logique puisqu'on utilise la première expression pour résoudre l'équation de Berkhoff de manière semi-analytique.
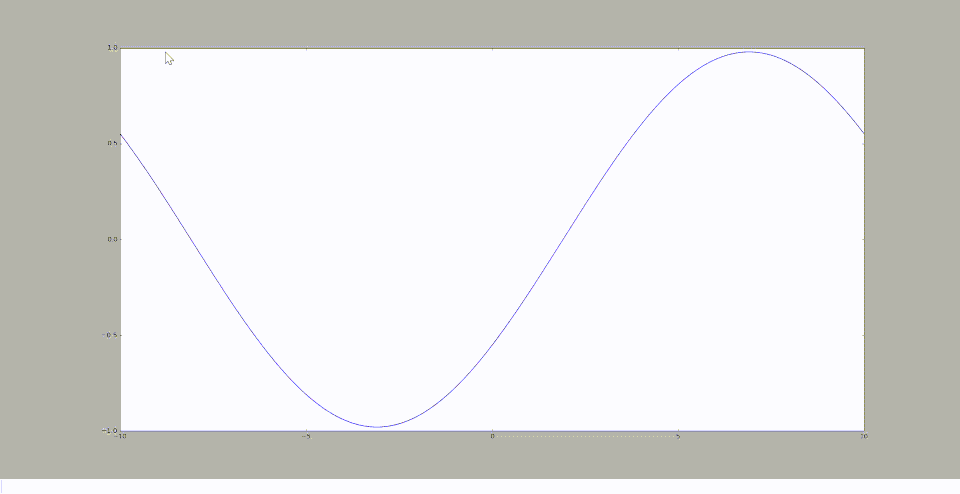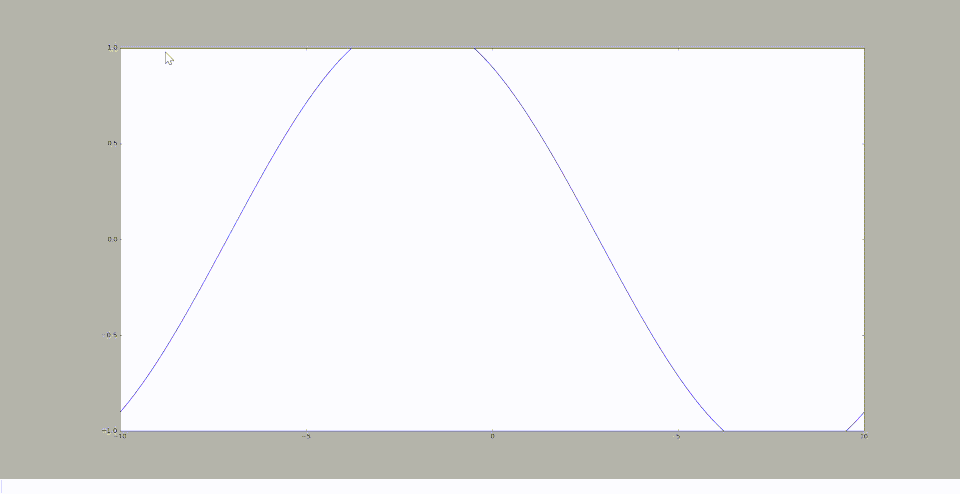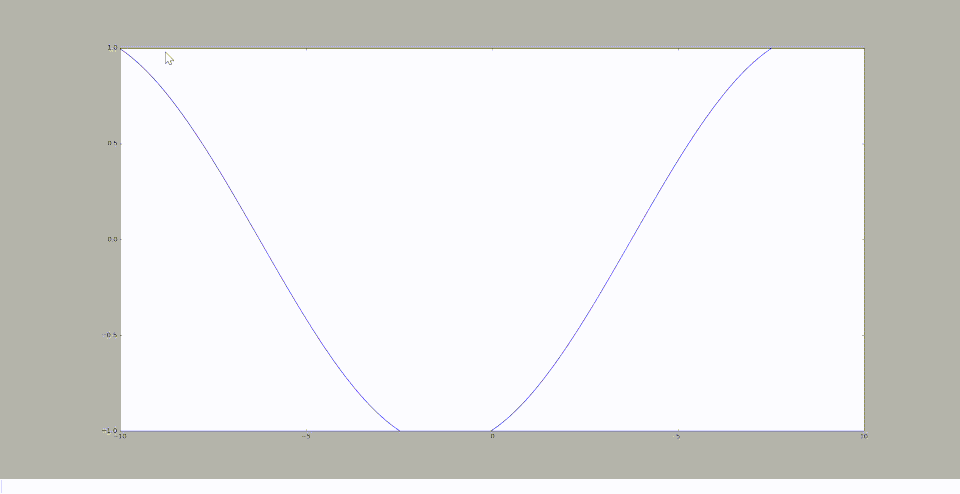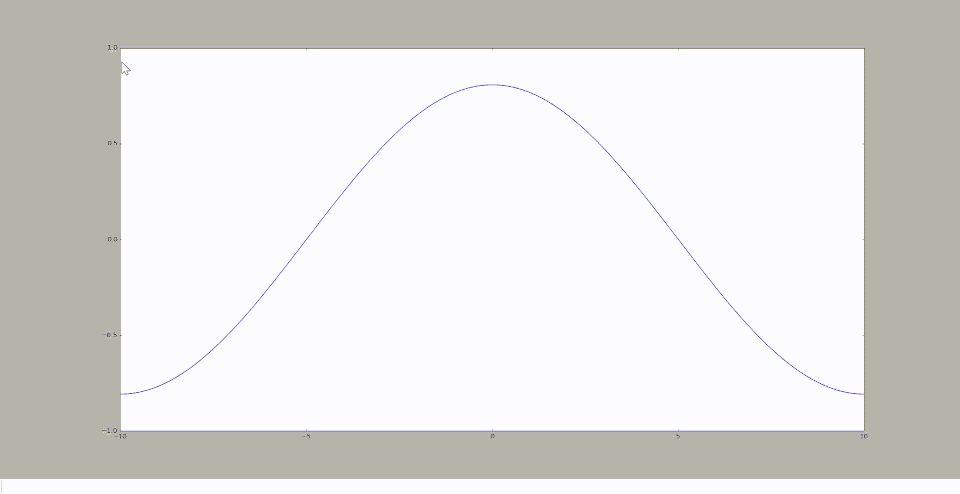
Homotopie
Représentation pour le cas n°2
Semblablement au cas n°1, on obtient l'équation suivante : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $
On obtient à l'aide de la méthode utilisée dans le cas n°1 (la méthode semi-analytique), le graphique suivant:
Homotopie pour le cas avec p=20
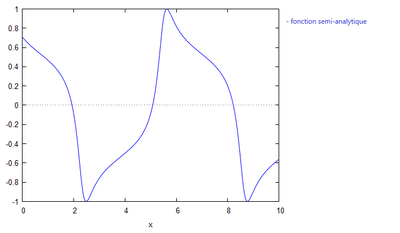
Etude de la sensibilité pour le cas n°2
En testant pour différentes valeurs de période, notée T, on obtient les graphiques suivants:
 T=10
T=10
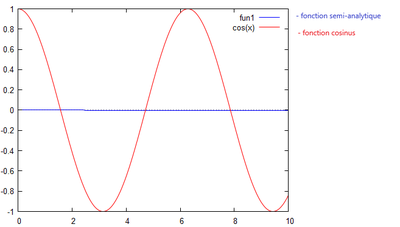
De cette observation, nous pouvons confirmer que plus T augmente, plus la courbe se rapproche d'une droite de pente nulle
Cas n°3
Dans le troisième cas, on s'intéresse à un domaine monodimensionnel de longueur L, avec cette fois une pente du fond constante avec entrée par l'aval d'une onde de fréquence unitaire. On considèrera que k=k0=cste
Solution analytique
On souhaite déterminer une solution analytique de l'équation de base transformée par changement de variable sous la forme d'une équation de type Bessel :
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $, avec $ C=\surd gH $ et $ CC_g=gH $
Contrairement au cas 1 et 2, H n'est plus constante : $ H(x)=-sx+H_0 $, avec H_0 la hauteur initiale et s la pente du fond.
L'équation de Berkhoff devient alors $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $
On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
En prenant le changement de variable $ X=\dfrac{k}{s}(H_0-sx) $, on obtient : $ skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0 $
Une multiplication par X, et une division par sk permet alors d'obtenir une équation qui a la forme d'une équation de Bessel : $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $
La solution de cette équation est de la forme $ Φ(X) = A*J_0(X) + B*Y_0(X) $, avec $ J_0 $ la fonction de Bessel de première espèce et $ Y_0 $ la fonction de Bessel de seconde espèce.
D'après les conditions aux limites, avec $ Φ(X)=1 $ en aval et $ \frac{∂Φ}{∂x}=ikΦ(X) $ en amont , et sachant que $ X_0 = \frac{k}{s}H_0 $ et $ X_L = \frac{k}{s}(H_0 - sL) $, on obtient :
$ A=\frac{Y1(xL)−iY0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $ et $ B=\frac{J1(xL)+iJ0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $
Donc la solution analytique est: $ \boxed{Φ(x)=(A*J0(\dfrac{k}{s}(H_0-sx))+B*Y0(\dfrac{k}{s}(H_0-sx))} $
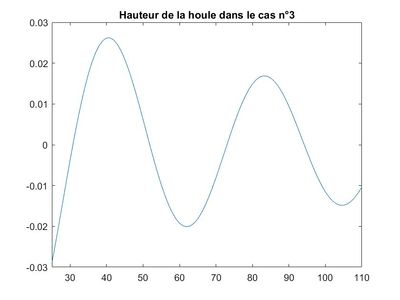
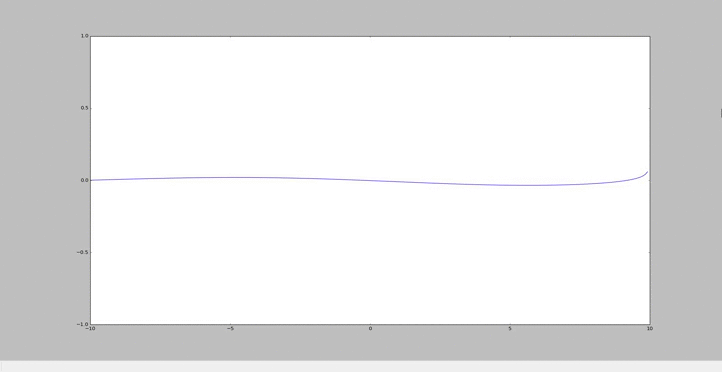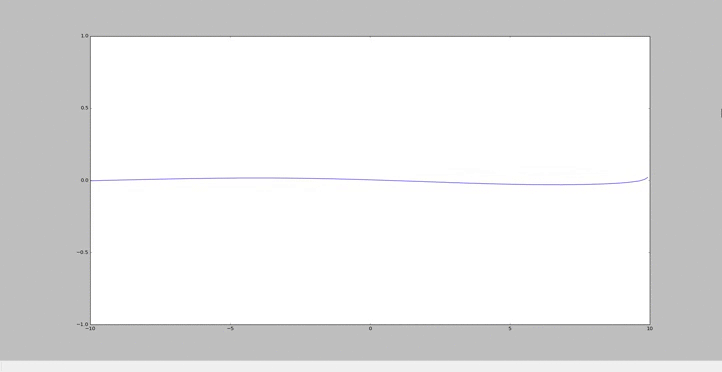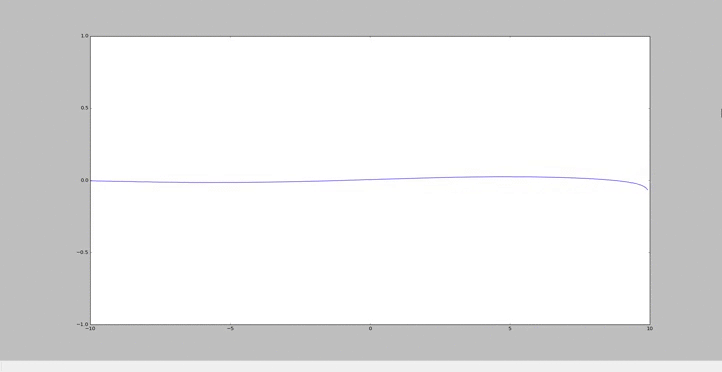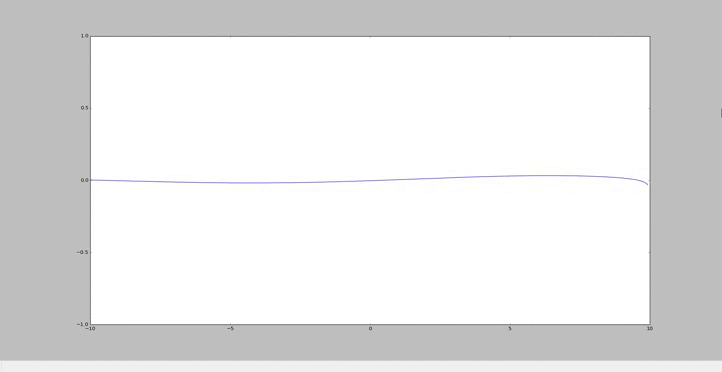
Homotopie
Particularité du cas n°3
Comme pour les précédents cas, on part de l'équation suivante : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
Afin de prendre en compte la pente, caractérisé par un k=k0, on pose $ r = \frac{s}{H_0} $
avec s, le coefficient de la pente.
On obtient alors: $ Φxx - pr*x*Φxx - pr*Φx + pk²(1-r*x)Φ = 0 $
Représentation pour le cas n°3
On obtient à l'aide de la méthode utilisée dans le cas n°1 (la méthode semi-analytique), le graphique suivant:
Homotopie pour le cas avec p=20
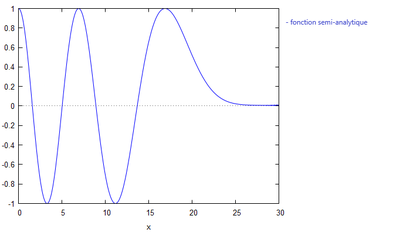
Etude de sensibilité pour le cas n°3
En testant pour différentes valeurs de profondeur, H0, nous avons observé les graphiques suivants:
 HO=0,5
HO=0,5
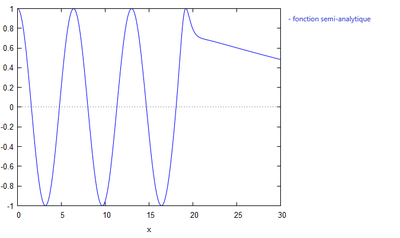
 H0=10
H0=10
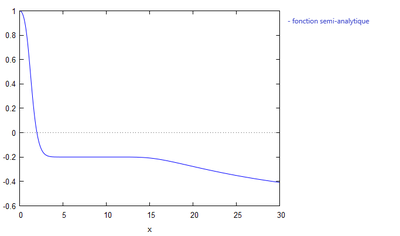
 H0=100
H0=100
De cette observation, nous pouvons confirmer que plus H0 augmente, plus la courbe met du temps à se stabiliser autour d'une valeur.
Cas n°6
Dans ce dernier cas on s'intéresse à un domaine bidimensionnel avec une bosse immergée parabolique sur le fond. On cherche à résoudre ce problème en coordonnées polaires puis en coordonnées cartésiennes.
Solution analytique
On part une nouvelle fois de l'équation de Berkhoff : $ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
En coordonnées polaires:
La solution analytique correspondant à la déformation d'un train d'onde régulière autour d'une bosse est fournie par l'expression suivante :
$ Φ(r,θ)=Φ_0\sum_{n=0}^{\infty}j^{n+1}ε_n\frac{J_n(kr)H'_n^1(kR)-J_n'(kR)H_n^1(kR)}{H'_n^1(kR)}cos(nθ) $
La hauteur de houle en tout point du domaine s'exprime de la manière suivante :
$ h(r,θ)=\mathbb{R}[Φ(r,θ)e^{jwt}] $
avec :
$ ε_n=2-δ_{n0} $
$ θ(r,θ) $: potentiel de houle
$ h(r,θ) $: hauteur de houle en coordonnées polaires repérée par rapport au centre de la bosse
$ h_0 $: hauteur de l'onde incidente
R : rayon de la bosse
T : période de l'onde
$ w=\frac{2π}{T} $
k : nombre d'onde
$ J_n $: fonctions de Bessel de 1ère espèce et d'ordre n
$ H_n^1 $: fonctions de Hankel de 1ère espèce et d'ordre n
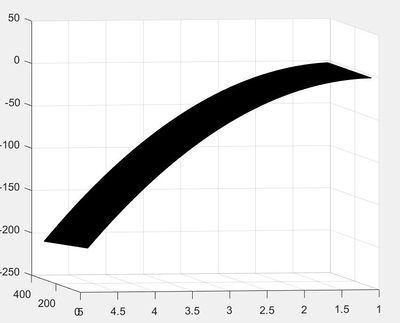
Nous n'avons pas réussi à obtenir un graphique ni un GIF satisfaisant pour ce cas. On observe seulement ce qui semble être le début d'une vague.
En coordonnées cartésiennes:
On exprime les coordonnées polaires en fonctions des coordonnées cartésiens.
$ r=\surd (x²+y²) $
$ θ=arccos(\frac{x}{\surd (x²+y²)}) $
La solution analytique correspondant à la déformation d'un train d'onde régulière autour d'une bosse est fournie par l'expression suivante :
$ Φ(x,y)=Φ_0\sum_{n=0}^{\infty}j^{n+1}ε_n\frac{J_n(k\surd (x²+y²))H'_n^1(kR)-J_n'(kR)H_n^1(kR)}{H'_n^1(kR)}cos(n*arccos(\frac{x}{\surd (x²+y²)})) $
La hauteur de houle en tout point du domaine s'exprime de la manière suivante :
$ h(x,y)=\mathbb{R}[Φ(x,y)e^{jwt}] $
Homotopie
Représentation du cas n°6
Dans un premier temps, nous avons essayé de représenter de manière monodimensionnelle la hauteur de la houle correspondant à ce cas, nous choisissons donc de positionner la bosse à une distance de 10m, symétrique de longueur 1,5 m.
On obtient à l'aide de la méthode utilisée dans le cas n°1 (la méthode semi-analytique), le graphique suivant:
Homotopie pour le cas avec p=20
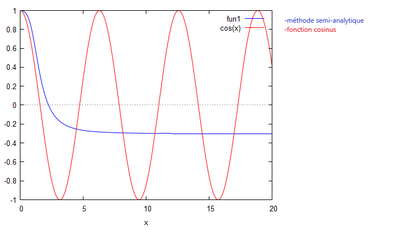
Cependant, il semblerait que le codage pour cette méthode ne fonctionne pas car nous supposons qu'au niveau de la bosse, la hauteur de la houle est censée augmentée.
Analyse des résultats et limites de chacun des modèles
Analyse des résultats
Nous remarquons que globalement les graphiques obtenues de manière analytique et homotopique, sont sensiblement semblables dans leur allure.
Dans le sujet, ces différents cas nous permettent de simuler les houles et donc de préciser les impacts de ces dernières sur des zones spécifiques. En analysant ces modélisations, il est donc possible de prévoir plus ou moins précisément les effets de la houle sur les littoraux.
Limites des modèles
limite physique
- Dans la réalité, les fonds sous-marins ne sont que rarement parfaitement plats, or cette condition participe dans nos résultats à cette impression de courbe lisse pour notre hauteur de houle.
- Dans la réalité, les vents superficielles vont impacter la forme des vagues et donc des houles ainsi qu'impacter la vitesse de ces dernières. Or l'une des hypothèses afin d'appliquer l'équation de Berkhoff est justement de négliger ce paramètre. Les modèles perdent donc en information.
limite numérique
- Tous les modèles traités dans cette page sont caractérisés par un domaine monodimensionnelle, or cela diminue la véracité du modèle utilisé. Dans une perspective de réalisme, il faut approfondir le cas n°6 : seul cas prenant en compte les irrégularités du fond marin.
 S'abonner à un flux RSS
S'abonner à un flux RSS