Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/APPAIX MOREL SANFRANCISCO : Différence entre versions
(→Solution analytique) |
(→Solution analytique) |
||
| Ligne 183 : | Ligne 183 : | ||
On cherche à mettre cette équation sous forme d'équation de Bessel de type : <math>x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0</math> | On cherche à mettre cette équation sous forme d'équation de Bessel de type : <math>x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0</math> | ||
<br /> | <br /> | ||
| − | En prenant le changement de variable <math>X=\dfrac{k}{s}(H_0-sx)</math>, on obtient: | + | En prenant le changement de variable <math>X=\dfrac{k}{s}(H_0-sx)</math>, on obtient : <math>skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0</math> |
| − | + | ||
| − | <math>skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0</math> | + | |
<br /> | <br /> | ||
<br /> | <br /> | ||
Version du 20 juin 2020 à 17:57
Bon courage et n'hésitez pas à communiquer avec moi par mail: jm.tanguy@shf-hydro.org
Sommaire |
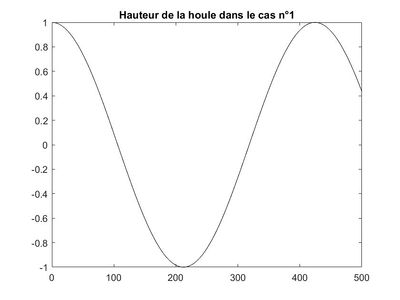
CAS n°1
Éléments de contexte
Modélisation mathématique des phénomènes de transport - évolution des fonds
Hiérarchie des hypothèses simplificatrices
Navier-Stokes
- l'eau est considéré comme un fluide incompressible
- on réalise une intégration sur une section de calcul rectangulaire
- on considère que l'accélération est négligeable
- on considère que le frottement est négligeable
SUITE DE CALCUL
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ(x)=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 et x = L : $ Φ(x)=1 $ et $ \frac{∂Φ(x)}{∂x}=ikΦ $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ikΦ(0)=ik=-ikA+ikB $ (dérivée 1ère ici ?)
$ \Leftrightarrow\ A+B=1 $ et $ B-A=1 $ donc $ A=0 $ et $ B=1 $
Donc la solution analytique est $ Φ(x)=e^{ikx} $
Homotopie
On a $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
En première estimation on pose $ u_0=1 $
$ (1-p)(Φ_{xx}-u_{0,xx})+p(Φ_{xx}+k^2Φ)=0 $ et $ Φ_{xx}+k^2Φ=0 $ car H est constant
On développe cette expression pour différents ordres de p et pour $ u_0=1 $ donc $ u_{0,xx}=0 $ puis on intègre ces équations en fonction des conditions aux limites :
Ordre 0 :
$ Φ_{0,xx}(x)-u_{0,xx}(x)-pΦ_{0,xx}(x)+pu_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0 $
$ \LeftrightarrowΦ_{0,xx}(x)-u_{0,xx}(x)+pu_{0,xx}(x)+pk^2Φ_0(x)=0 $ cette égalité est vraie pour tout p, donc en particulier pour p=0 donc :
$ Φ_{0,xx}(x)-u_{0,xx}(x)=0 $
$ \int_0^L Φ_{0,xx}(x)dx = A.... $
Ordre 1 :
$ Φ_{0,xx}(x)-u_{0,xx}(x)+pΦ_{1,xx}(x)+pu_{0,xx}(x)-pΦ_{0,xx}(x)-p^2Φ_{1,xx}(x)+pΦ_{0,xx}(x)+p^2Φ_{1,xx}(x)+pk^2Φ_0(x)+p^2k^2Φ_1(x)=0 $
On intègre ensuite chaque équation en fonction des conditions aux limites.
Ordre 0:
$ Φ_{0}(x)=u_{0}+Ax+B $:deux constantes à déterminer
Conditions aux limites:
1) en x=0, $ Φ=1 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=A $
et $ Φx(x=L)=ikΦ(x=L)=ik(u0+AL) $
donc $ A=ik(u0+AL) $
D'où $ A=\frac{iku0}{1-ikL} $;
Et on obtient $ Φ0(x)=u0+Ax=u0+\frac{iku0}{1-ikL}*x $
Avec u0=1, on a alors:
$ Φ0(x)=1+Ax=1+\frac{ik}{1-ikL}*x $
Ordre 1:
$ Φ1+u0+k²∫∫Φ0+A2+B2=0 $
On injecte dans l'équation ci-dessus l'expression de Φ0.
On a alors:
$ Φ1+u0+k²(\frac{u0x²}{2}+[\frac{iku0}{1-ikL}]\frac{x³}{3})+A2+B2=0 $
Conditions aux limites:
1) en x=0, $ Φ=1 $ donne: $ B=-2 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=-k²(u0L+[\frac{iku0}{1-ikL}]L²/2)-A2 $
et $ Φx(x=L)=ikΦ(x=L)=-ik(u0+k²(u0x²/2+[iku0/(1-ikL)]\frac{x³}{3})+A2-2) $ donc $ A=ik(u0+AL) $
donc, par identification, $ A2=k[k(u0L+[iku0/(1-ikL)]\frac{L²}{2})-i(u0+k²(u0x²/2+[\frac{iku0}{1-ikL}]x³/3)-2)]*1/(L-1) $
Avec u0=1, on a alors:
$ A2=k[k(L+[\frac{ik}{1-ikL}]\frac{L²}{2})-i(k²(\frac{x²}{2}+[\frac{ik}{1-ikL}]x³/3)-2)]*1/(L-1) $
Ordre 2:
$ Φ2+k²∫∫Φ1+A3+B3=0 $
On injecte dans l'équation ci-dessus l'expression de Φ1.
On a alors:
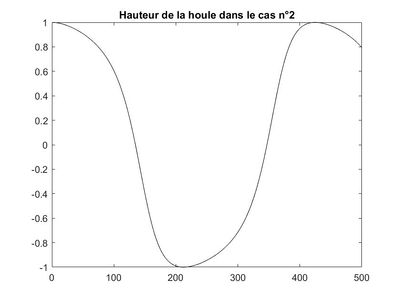
CAS n°2
Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0.
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 : $ \frac{∂Φ(x)}{∂x}=ik(2-Φ) $
en x = L : $ \frac{∂Φ(x)}{∂x}=0 $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ik(2-Φ(0))=ik $
On trouve donc $ A=\frac{e^{ikL}}{2cos(kL)} $ et $ B=1-\frac{e^{ikL}}{2cos(kL)} $
Donc $ Φ=\frac{e^{ikL}}{2cos(kL)}e^{-ikx}+(1-\frac{e^{ikL}}{2cos(kL)})e^{ikx} $
Homotopie
Comme pour le cas 1, on a : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $
Comme seules les conditions aux limites changent, on aura les mêmes équations aux constantes près.
Cas n°3
Dans le troisième cas, on s'intéresse à un domaine monodimensionnel de longueur L, avec cette fois une pente du fond constante avec entrée par l'aval d'une onde de fréquence unitaire. On considèrera que k=k0=cste
Solution analytique
On souhaite déterminer une solution analytique de l'équation de base transformée par changement de variable sous la forme d'une équation de type Bessel :
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $, avec $ C=\surd gH $ et $ CC_g=gH $
Mais contrairement au cas 1 et 2, H n'est plus constante : $ H(x)=-sx+H_0 $, avec H_0 la hauteur initiale et s la pente du fond.
L'équation de Berkhoff devient alors $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $
On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
En prenant le changement de variable $ X=\dfrac{k}{s}(H_0-sx) $, on obtient : $ skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0 $
Une multiplication par X, et une division par sk permet alors d'obtenir une équation qui a la forme d'une équation de Bessel : $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $
La solution de cette équation est de la forme $ Φ(X) = A*J_0(X) + B*Y_0(X) $, avec $ J_0 $ la fonction de Bessel de première espèce et $ Y_0 $ la fonction de Bessel de seconde espèce.
D'après les conditions aux limites, avec $ Φ(X)=1 $ en aval et $ \frac{∂Φ}{∂x}=ikΦ(X) $ en amont , et sachant que $ X_0 = \frac{k}{s}H_0 $ et $ X_L = \frac{k}{s}(H_0 - sL) $, on obtient :
$ A=\frac{Y1(xL)−iY0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $ et $ B=\frac{J1(xL)+iJ0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $
Donc la solution analytique est: $ Φ(x)=(A*J0(\dfrac{k}{s}(H_0-sx))+B*Y0(\dfrac{k}{s}(H_0-sx)) $
Homotopie
Comme pour le cas 1 et 2, on cherche une solution semi-analytique.
On a une nouvelle fois : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
En considérant $ r = \frac{s}{H_0} $, on obtient alors: $ Φxx - pr*x*Φxx - pr*Φx + pk²(1-r*x)Φ = 0 $
Ordre 0:
Ordre 1:
Cas n°6
Dans ce dernier cas on s'intéresse à un domaine bidimensionnel avec une bosse immergée parabolique sur le fond. On cherche à résoudre ce problème en coordonnées polaires puis en coordonnées cartésiennes.
Solution analytique
On part une nouvelle fois de l'équation de Berkhoff : $ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
La solution analytique correspondant à la déformation d'un train d'onde régulière autour d'une bosse est fournie par l'expression suivante :
$ Φ(r,θ)=Φ_0sum_{n=0}^{infty}j^{n+1}ε_n\frac{J_n(kr)H'_n^1(kR)-J_n'(kR)H_n^1(kR)}{H'_n^1(kR)}cos(nθ) $ (pb somme)
La hauteur de houle en tout point du domaine s'exprime de la manière suivante :
$ h(r,θ)=\mathbb{R}[Φ(r,θ)e^{jwt}] $
avec :
$ ε_n=2-δ_{n0} $
$ θ(r,θ) $: potentiel de houle
$ h(r,θ) $: hauteur de houle en coordonnées polaires repérée par rapport au centre de la bosse
$ h_0 $: hauteur de l'onde incidente
R : rayon de la bosse
T : période de l'onde
$ w=\frac{2π}{T} $
k : nombre d'onde
$ J_n $: fonctions de Bessel de 1ère espèce et d'ordre n
$ H_n^1 $: fonctions de Hankel de 1ère espèce et d'ordre n
Début sol analytique
Expression de l'équation simplifiée
A partir des hypothèses précédentes, considérons un canal infini de forme rectangulaire : largeur b et profondeur d'eau H0.
Soit h le niveau d'eau, u la vitesse moyenne de l'écoulement dans la section de surface A=bH0 et enfin Q=bH0u le débit.
SCHEMA
On obtient alors les deux équations suivantes :
$ b∂h/∂t + ∂Q/∂x = 0 $ (1)
$ ∂Q/∂t + gA(∂h/∂x) = 0 $ (2)
Solution analytique
On dérive alors (1) par rapport à t et (2) par rapport à x.
$ b×∂²h/∂t² + ∂²Q/∂x∂t = 0 $ (1)
$ δ²Q/δxδt + gA(∂²h/∂²x) = 0 $ (2)
On élimine ensuite le terme $ ∂²Q/∂x∂t $, nous obtenons l'équation des ondes suivante: $ -∂²h/∂t² + gH0∂²h/∂x² = 0 $
Cette équation peut se mettre sous la forme: $ (∂h∂t+c∂h∂x)=0 $
Une solution de cette équation pour l'évolution de la surface libre est la suivante:
$ h=acos(kx−σt) $ qui correspond à la propagation de 2 ondes de vitesse $ c=√gH $ dans les deux sens (vers la gauche et vers la droite)
Soit k le nombre d'onde, on obtient alors:
$ ∂h/∂t = aσsin(kx - σt) $ et $ ∂²h/∂t² = -σ²h(x,t) $
Donc $ -σ²h(x,t) + gH0 × ∂²h/∂x² = 0 $
Donc $ h(x,t)=A.exp(xσ/c)+B.exp(-xσ/c) $ avec A et B, deux constantes.
SUITE DE CALCUL
Cas d'application
Onde de marée progressive
Le cas que nous présentons ici est un cas d'école, car il met en scène la propagation d'une onde de marée de période de 12 heures dans un canal rectangulaire.
Les caractéristiques de cet exemple sont les suivants:
- période de la marée (T) : 12 heures
- amplitude : ... m
- profondeur (H0): 500 m
Les calculs conduisent à :
- célérité (c): 70 m/s
- nombre d'onde (k) : 7,48E-003 m-1
On résout l'équation de Berkhoff
 S'abonner à un flux RSS
S'abonner à un flux RSS