Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/APPAIX MOREL SANFRANCISCO : Différence entre versions
| Ligne 46 : | Ligne 46 : | ||
=== Homotopie === | === Homotopie === | ||
| − | + | ==== La méthode semi-analytique ==== | |
| + | La méthode semi-analytique consiste à résoudre l'équation de Bessel en approchant au mieux la solution analytique | ||
| + | Ici afin de résoudre de manière semi-analytique l'équation, il est nécessaire de <span style="color: Blue;">coder la démarche de l'homotopie. | ||
| + | |||
| + | ===== Resoudre à la main les deux premiers cas ===== | ||
| + | D'après la formule, on obtient : | ||
| + | <br /> | ||
| + | <math>Φ=\sum_{k=0}^{\infty} p^kΦ_k</math> et <math>Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx}</math> | ||
<br /> | <br /> | ||
| − | En première estimation on pose <math>u_0= | + | En première estimation on pose <math>u_0=0</math> |
<br /> | <br /> | ||
| − | <math>(1-p)(Φ_{xx}-u_{0,xx})+p(Φ_{xx}+k^2Φ)=0</math> et <math>Φ_{xx}+k^2Φ=0</math> car H est constant | + | <math>(1-p)(Φ_{xx}-u_{0,xx})+p(Φ_{xx}+k^2Φ)=0</math> et <math>Φ_{xx}+k^2Φ=0</math> car H est constant dans le premier cas |
<br /> | <br /> | ||
| − | On développe cette expression pour différents ordres de p | + | On développe cette expression pour différents ordres de p ( <math>u_{0,xx}=0</math> ) puis on intègre ces équations en fonction des conditions aux limites : |
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | + | Pour l'ordre 0 : | |
<br /> | <br /> | ||
<math>Φ_{0,xx}(x)-u_{0,xx}(x)-pΦ_{0,xx}(x)+pu_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0</math> | <math>Φ_{0,xx}(x)-u_{0,xx}(x)-pΦ_{0,xx}(x)+pu_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0</math> | ||
| Ligne 61 : | Ligne 68 : | ||
<math> \LeftrightarrowΦ_{0,xx}(x)-u_{0,xx}(x)+pu_{0,xx}(x)+pk^2Φ_0(x)=0</math> cette égalité est vraie pour tout p, donc en particulier pour p=0 donc : | <math> \LeftrightarrowΦ_{0,xx}(x)-u_{0,xx}(x)+pu_{0,xx}(x)+pk^2Φ_0(x)=0</math> cette égalité est vraie pour tout p, donc en particulier pour p=0 donc : | ||
<br /> | <br /> | ||
| − | <math>Φ_ | + | <math>Φ_{0,xx}(x)=0</math> |
<br /> | <br /> | ||
| + | En intégrant deux fois, on obtient : | ||
<br /> | <br /> | ||
| − | <math>\int_0^L Φ_{0,xx}(x)dx = | + | <math>\int_0^L Φ_{0,xx}(x)dx = Ax + B</math>, avec A et B deux constantes à déterminer |
<br /> | <br /> | ||
| − | + | Or le sujet nous dit qu'à l'ordre 0, les conditions aux limites sont: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<br /> | <br /> | ||
1) en x=0, <math>Φ=1</math> donne: <math>B=0</math> | 1) en x=0, <math>Φ=1</math> donne: <math>B=0</math> | ||
| Ligne 84 : | Ligne 80 : | ||
2) en x=L, <math>Φx=ikΦ</math> donne <math>Φx=A</math> | 2) en x=L, <math>Φx=ikΦ</math> donne <math>Φx=A</math> | ||
<br /> | <br /> | ||
| − | et <math>Φx(x=L)=ikΦ(x=L)=ik( | + | et <math>Φx(x=L)=ikΦ(x=L)=ik(AL)</math> |
<br /> | <br /> | ||
donc <math>A=ik(u0+AL)</math> | donc <math>A=ik(u0+AL)</math> | ||
| Ligne 90 : | Ligne 86 : | ||
D'où <math>A=\frac{iku0}{1-ikL}</math>; | D'où <math>A=\frac{iku0}{1-ikL}</math>; | ||
<br /> | <br /> | ||
| − | Et on obtient <math>Φ0(x)= | + | Et on obtient <span style="color: Green;"><math>Φ0(x)=Ax=\frac{iku0}{1-ikL}*x</math> |
<br /> | <br /> | ||
| − | + | ||
| + | Pour passer aux différents ordres, il suffira de réaliser une <span style="color: Blue;">récurrence en faisant comme dans l'ordre 1 c'est-à-dire résoudre: | ||
<br /> | <br /> | ||
| − | <math> | + | <math>Φ1+k²∫∫Φ0+A2*x+B2=0</math> ( ce qui donne à l'ordre n : <span style="color: Green;"><math>Φn+k²∫∫Φn-1+A'*x+B'=0</math> ) |
<br /> | <br /> | ||
| − | + | On injecte dans l'équation ci-dessus l'expression de Φ0 trouvée précédemment. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | On injecte dans l'équation ci-dessus l'expression de Φ0. | + | |
<br /> | <br /> | ||
On a alors: | On a alors: | ||
| − | <math>Φ1 | + | <math>Φ1+k²([\frac{ik}{1-ikL}]\frac{x³}{3})+A2*x+B2=0</math> |
<br /> | <br /> | ||
| − | + | Or le sujet nous dit qu'à partir de l'ordre 1, les conditions aux limites sont: | |
<br /> | <br /> | ||
| − | 1) en x=0, <math>Φ= | + | 1) en x=0, <math>Φ=0</math> donne: <math>B=0</math> |
<br /> | <br /> | ||
| − | 2) en x=L, <math>Φx=ikΦ</math> donne <math>Φx=-k²( | + | 2) en x=L, <math>Φx=ikΦ</math> donne <math>Φx=-k²([\frac{ik}{1-ikL}]frac{L²}{2}]-A2</math> |
<br /> | <br /> | ||
| − | et <math>Φx(x=L)=ikΦ(x=L)=-ik( | + | et <math>Φx(x=L)=ikΦ(x=L)=-ik(-k²([ik/(1-ikL)]\frac{L³}{3})+A2*L)</math> |
<br /> | <br /> | ||
| − | donc, par identification, <math>A2= | + | donc, par identification et en généralisant, on peut dire que <math>A2=[\frac{ikΦxx - Φx}{1-ikL}]frac{L²}{2}]</math> |
<br /> | <br /> | ||
| − | + | C'est cette formule de A qu'il faut rentrer dans votre code afin d'obtenir le graphique suivant pour : | |
<br /> | <br /> | ||
| − | + | [[File:homotopie_1.png|400px]] | |
<br /> | <br /> | ||
| + | |||
| + | ===== Codage ===== | ||
| + | Pour coder votre méthode semi-analytique suivez les étapes réalisées dans la Résolution à la main | ||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== CAS n°2 == | == CAS n°2 == | ||
Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0. | Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0. | ||
Version du 21 juin 2020 à 00:05
Bon courage et n'hésitez pas à communiquer avec moi par mail: jm.tanguy@shf-hydro.org
Sommaire |
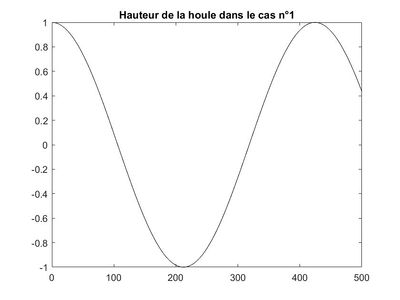
CAS n°1
Éléments de contexte
Modélisation mathématique des phénomènes de transport - évolution des fonds
Hiérarchie des hypothèses simplificatrices
Navier-Stokes
- l'eau est considéré comme un fluide incompressible
- on réalise une intégration sur une section de calcul rectangulaire
- on considère que l'accélération est négligeable
- on considère que le frottement est négligeable
SUITE DE CALCUL
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ(x)=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 et x = L : $ Φ(x)=1 $ et $ \frac{∂Φ(x)}{∂x}=ikΦ $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ikΦ(0)=ik=-ikA+ikB $ (dérivée 1ère ici ?)
$ \Leftrightarrow\ A+B=1 $ et $ B-A=1 $ donc $ A=0 $ et $ B=1 $
Donc la solution analytique est $ \boxed{Φ(x)=e^{ikx}} $
Homotopie
La méthode semi-analytique
La méthode semi-analytique consiste à résoudre l'équation de Bessel en approchant au mieux la solution analytique Ici afin de résoudre de manière semi-analytique l'équation, il est nécessaire de coder la démarche de l'homotopie.
Resoudre à la main les deux premiers cas
D'après la formule, on obtient :
$ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
En première estimation on pose $ u_0=0 $
$ (1-p)(Φ_{xx}-u_{0,xx})+p(Φ_{xx}+k^2Φ)=0 $ et $ Φ_{xx}+k^2Φ=0 $ car H est constant dans le premier cas
On développe cette expression pour différents ordres de p ( $ u_{0,xx}=0 $ ) puis on intègre ces équations en fonction des conditions aux limites :
Pour l'ordre 0 :
$ Φ_{0,xx}(x)-u_{0,xx}(x)-pΦ_{0,xx}(x)+pu_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0 $
$ \LeftrightarrowΦ_{0,xx}(x)-u_{0,xx}(x)+pu_{0,xx}(x)+pk^2Φ_0(x)=0 $ cette égalité est vraie pour tout p, donc en particulier pour p=0 donc :
$ Φ_{0,xx}(x)=0 $
En intégrant deux fois, on obtient :
$ \int_0^L Φ_{0,xx}(x)dx = Ax + B $, avec A et B deux constantes à déterminer
Or le sujet nous dit qu'à l'ordre 0, les conditions aux limites sont:
1) en x=0, $ Φ=1 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=A $
et $ Φx(x=L)=ikΦ(x=L)=ik(AL) $
donc $ A=ik(u0+AL) $
D'où $ A=\frac{iku0}{1-ikL} $;
Et on obtient $ Φ0(x)=Ax=\frac{iku0}{1-ikL}*x $
Pour passer aux différents ordres, il suffira de réaliser une récurrence en faisant comme dans l'ordre 1 c'est-à-dire résoudre:
$ Φ1+k²∫∫Φ0+A2*x+B2=0 $ ( ce qui donne à l'ordre n : $ Φn+k²∫∫Φn-1+A'*x+B'=0 $ )
On injecte dans l'équation ci-dessus l'expression de Φ0 trouvée précédemment.
On a alors:
$ Φ1+k²([\frac{ik}{1-ikL}]\frac{x³}{3})+A2*x+B2=0 $
Or le sujet nous dit qu'à partir de l'ordre 1, les conditions aux limites sont:
1) en x=0, $ Φ=0 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=-k²([\frac{ik}{1-ikL}]frac{L²}{2}]-A2 $
et $ Φx(x=L)=ikΦ(x=L)=-ik(-k²([ik/(1-ikL)]\frac{L³}{3})+A2*L) $
donc, par identification et en généralisant, on peut dire que $ A2=[\frac{ikΦxx - Φx}{1-ikL}]frac{L²}{2}] $
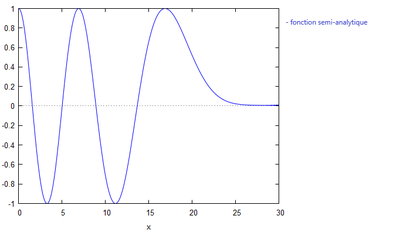
C'est cette formule de A qu'il faut rentrer dans votre code afin d'obtenir le graphique suivant pour :
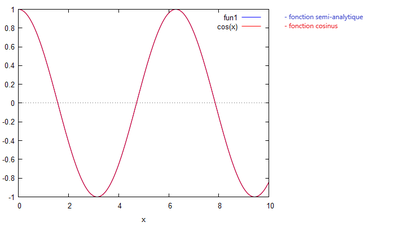
Codage
Pour coder votre méthode semi-analytique suivez les étapes réalisées dans la Résolution à la main
CAS n°2
Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0.
Solution analytique
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :
$ Φ=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 : $ \frac{∂Φ(x)}{∂x}=ik(2-Φ) $
en x = L : $ \frac{∂Φ(x)}{∂x}=0 $
$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ik(2-Φ(0))=ik $
On trouve donc $ A=\frac{e^{ikL}}{2cos(kL)} $ et $ B=1-\frac{e^{ikL}}{2cos(kL)} $
Donc la solution analytique est $ \boxed{Φ=\frac{e^{ikL}}{2cos(kL)}e^{-ikx}+(1-\frac{e^{ikL}}{2cos(kL)})e^{ikx}} $
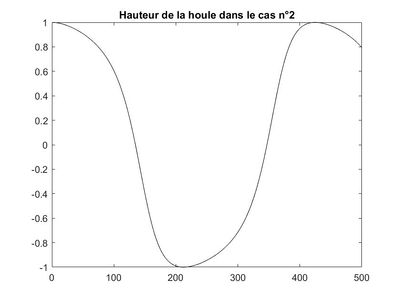
Homotopie
Comme pour le cas 1, on a : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $
Comme seules les conditions aux limites changent, on aura les mêmes équations aux constantes près.
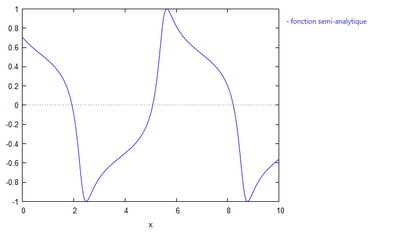
On obtient donc le graphique suivant :
Cas n°3
Dans le troisième cas, on s'intéresse à un domaine monodimensionnel de longueur L, avec cette fois une pente du fond constante avec entrée par l'aval d'une onde de fréquence unitaire. On considèrera que k=k0=cste
Solution analytique
On souhaite déterminer une solution analytique de l'équation de base transformée par changement de variable sous la forme d'une équation de type Bessel :
$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $, avec $ C=\surd gH $ et $ CC_g=gH $
Mais contrairement au cas 1 et 2, H n'est plus constante : $ H(x)=-sx+H_0 $, avec H_0 la hauteur initiale et s la pente du fond.
L'équation de Berkhoff devient alors $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $
On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
En prenant le changement de variable $ X=\dfrac{k}{s}(H_0-sx) $, on obtient : $ skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0 $
Une multiplication par X, et une division par sk permet alors d'obtenir une équation qui a la forme d'une équation de Bessel : $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $
La solution de cette équation est de la forme $ Φ(X) = A*J_0(X) + B*Y_0(X) $, avec $ J_0 $ la fonction de Bessel de première espèce et $ Y_0 $ la fonction de Bessel de seconde espèce.
D'après les conditions aux limites, avec $ Φ(X)=1 $ en aval et $ \frac{∂Φ}{∂x}=ikΦ(X) $ en amont , et sachant que $ X_0 = \frac{k}{s}H_0 $ et $ X_L = \frac{k}{s}(H_0 - sL) $, on obtient :
$ A=\frac{Y1(xL)−iY0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $ et $ B=\frac{J1(xL)+iJ0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $
Donc la solution analytique est: $ \boxed{Φ(x)=(A*J0(\dfrac{k}{s}(H_0-sx))+B*Y0(\dfrac{k}{s}(H_0-sx))} $
Homotopie
Comme pour le cas 1 et 2, on cherche une solution semi-analytique.
On a une nouvelle fois : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
En considérant $ r = \frac{s}{H_0} $, on obtient alors: $ Φxx - pr*x*Φxx - pr*Φx + pk²(1-r*x)Φ = 0 $
En suivant, la même méthode que précédemment, on obtient le graphique suivant :
Cas n°6
Dans ce dernier cas on s'intéresse à un domaine bidimensionnel avec une bosse immergée parabolique sur le fond. On cherche à résoudre ce problème en coordonnées polaires puis en coordonnées cartésiennes.
Solution analytique
On part une nouvelle fois de l'équation de Berkhoff : $ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $
on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $
La solution analytique correspondant à la déformation d'un train d'onde régulière autour d'une bosse est fournie par l'expression suivante :
$ Φ(r,θ)=Φ_0sum_{n=0}^{infty}j^{n+1}ε_n\frac{J_n(kr)H'_n^1(kR)-J_n'(kR)H_n^1(kR)}{H'_n^1(kR)}cos(nθ) $ (pb somme)
La hauteur de houle en tout point du domaine s'exprime de la manière suivante :
$ h(r,θ)=\mathbb{R}[Φ(r,θ)e^{jwt}] $
avec :
$ ε_n=2-δ_{n0} $
$ θ(r,θ) $: potentiel de houle
$ h(r,θ) $: hauteur de houle en coordonnées polaires repérée par rapport au centre de la bosse
$ h_0 $: hauteur de l'onde incidente
R : rayon de la bosse
T : période de l'onde
$ w=\frac{2π}{T} $
k : nombre d'onde
$ J_n $: fonctions de Bessel de 1ère espèce et d'ordre n
$ H_n^1 $: fonctions de Hankel de 1ère espèce et d'ordre n
 S'abonner à un flux RSS
S'abonner à un flux RSS