Utilisateur:Jean-Michel Tanguy/SujetENTPE2020/APPAIX MOREL SANFRANCISCO : Différence entre versions

Version du 21 juin 2020 à 19:08

CAS n°1

Dans le premier cas, on s'intéresse à un domaine monodimensionnel plat de longueur L avec des conditions aux limites suivantes : la condition de flux aval est Φ=1 et la condition de flux en amont est Φ_x=ikΦ.

Solution analytique

$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $

on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $

$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :

$ Φ(x)=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 et x = L : $ Φ(x)=1 $ et $ \frac{∂Φ(x)}{∂x}=ikΦ $

$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ikΦ(0)=ik=-ikA+ikB $ (dérivée 1ère ici ?)

$ \Leftrightarrow\ A+B=1 $ et $ B-A=1 $ donc $ A=0 $ et $ B=1 $

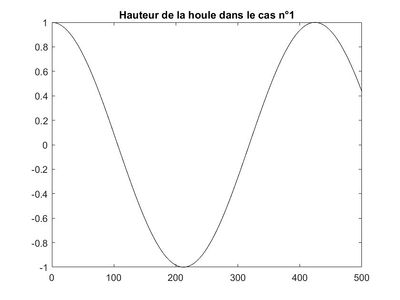
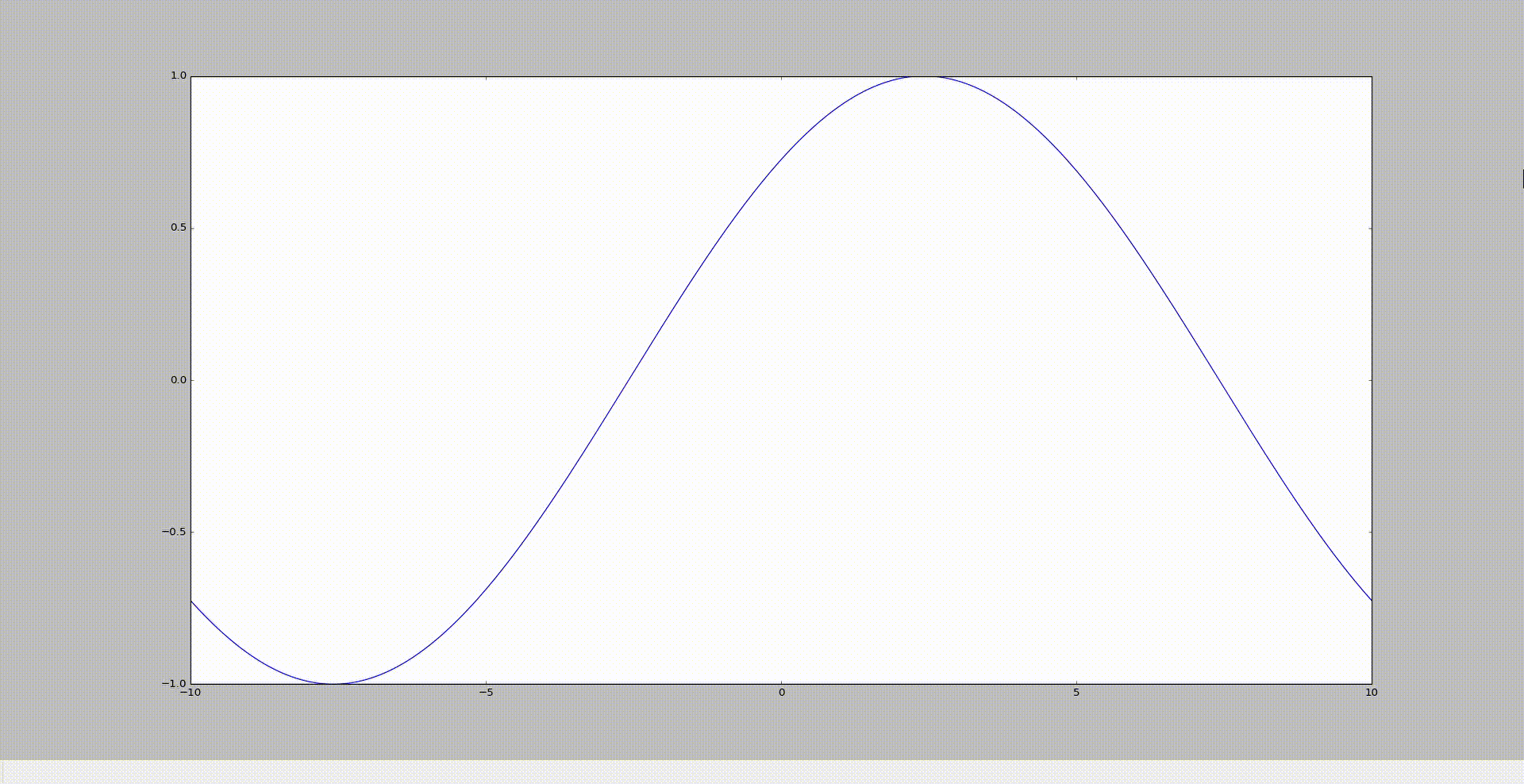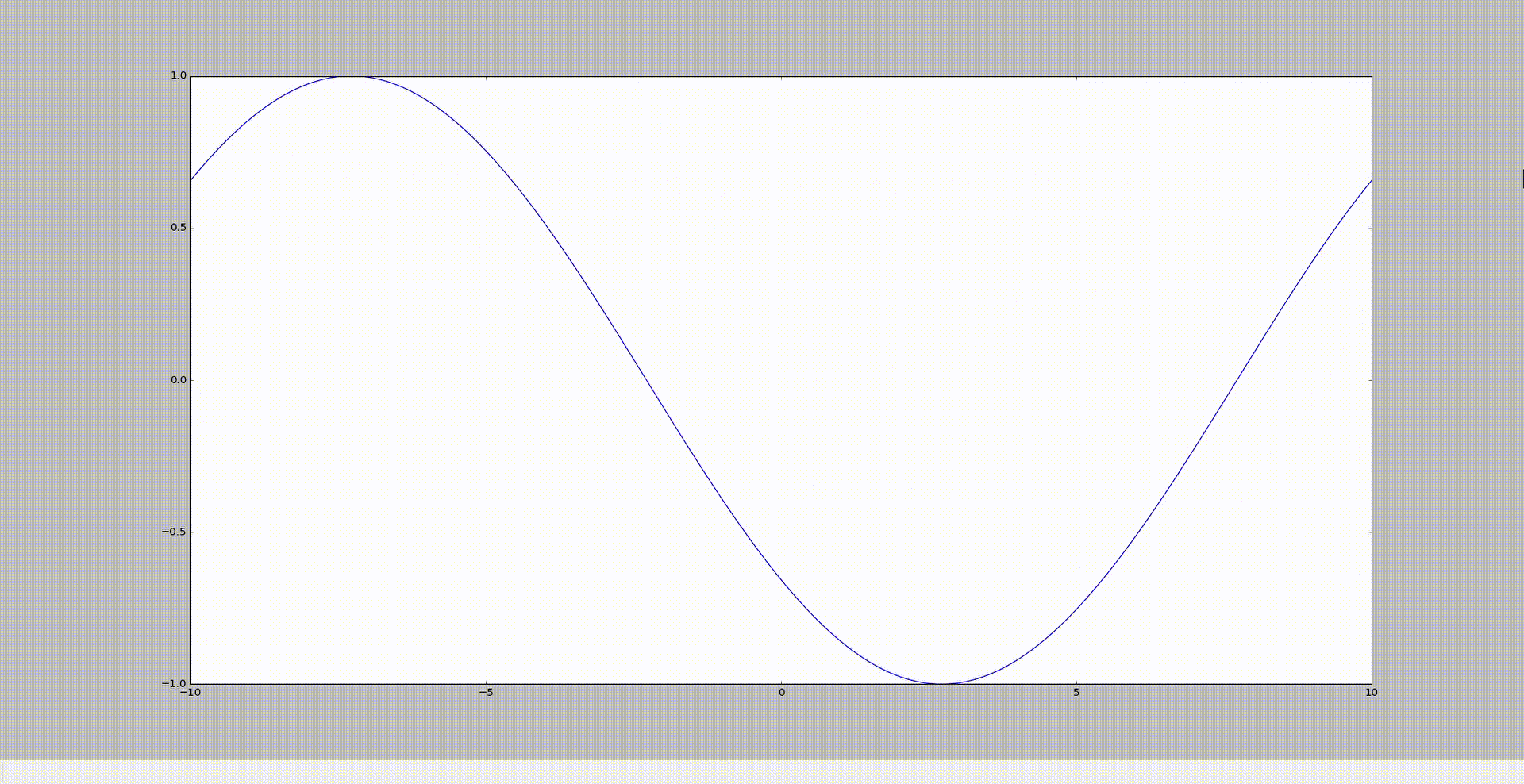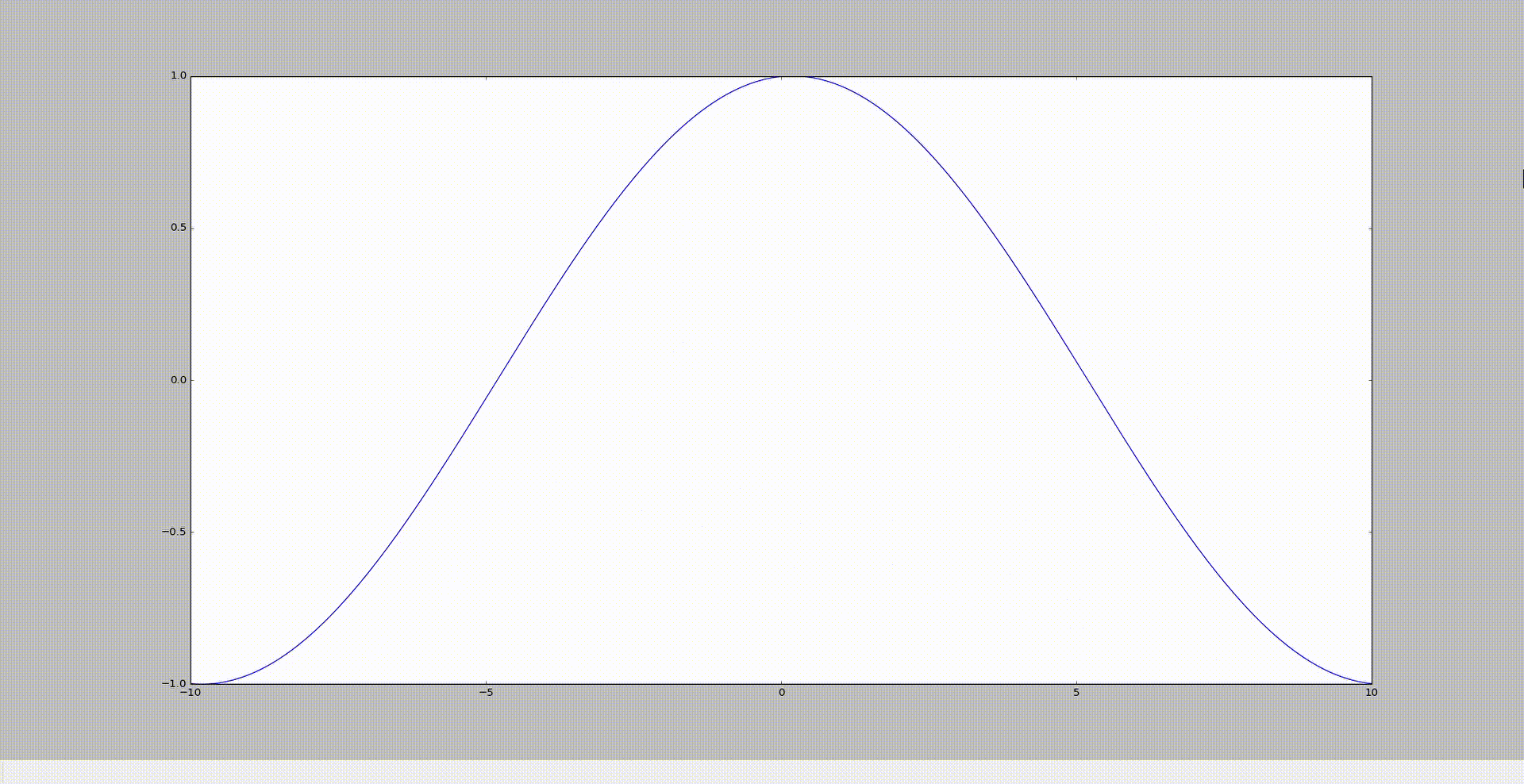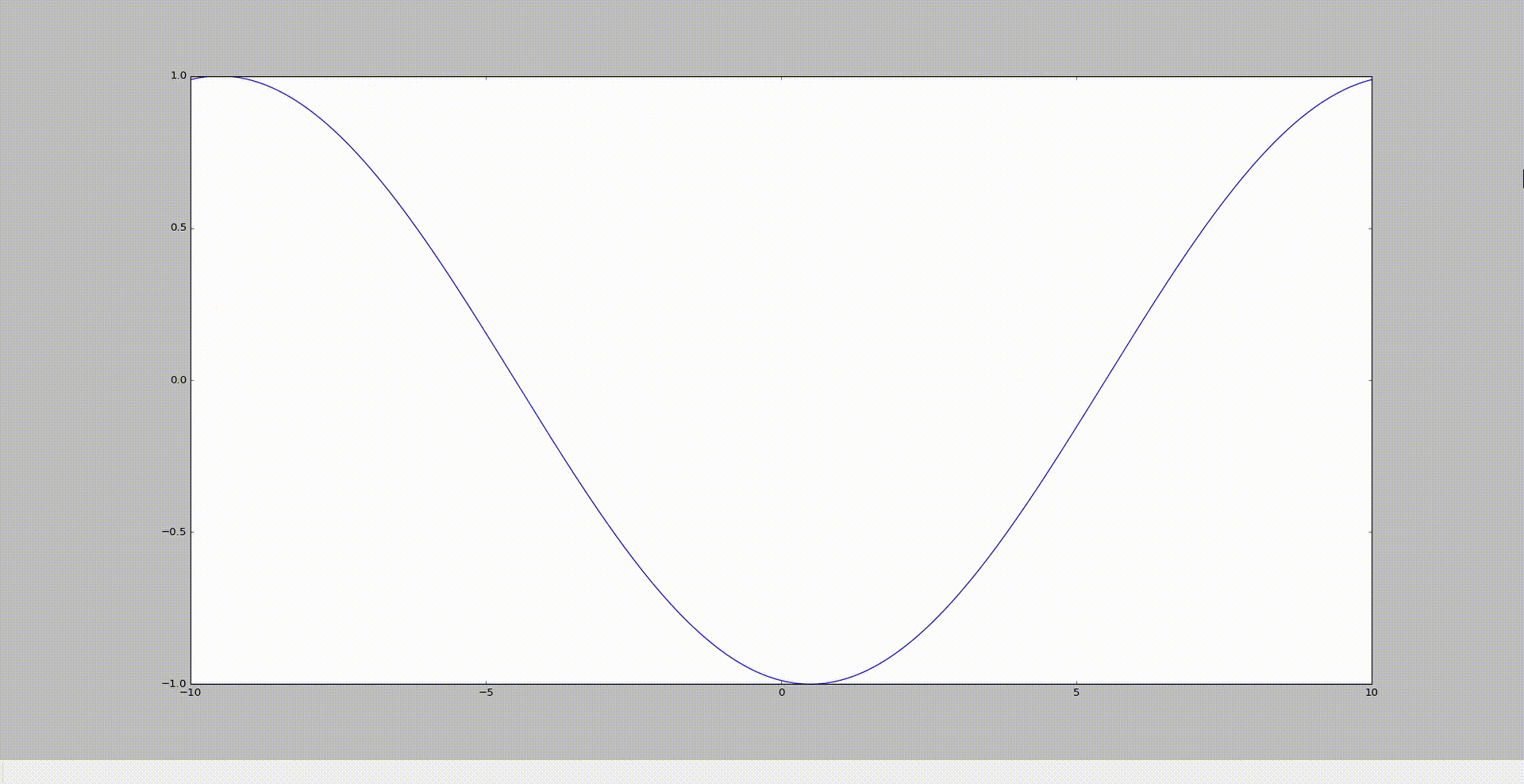
Donc la solution analytique est $ \boxed{Φ(x)=e^{ikx}} $

Homotopie

La méthode semi-analytique

La méthode semi-analytique consiste à résoudre l'équation de Bessel en approchant au mieux la solution analytique.
Ici afin de résoudre de manière semi-analytique l'équation, il est nécessaire de coder la démarche de l'homotopie.

1) Généralisez la formule de l'homotopie
D'après la formule, on obtient :
$ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $

2) poser une estimation pour u_0
En première estimation on pose $ u_0=0 $
$ (1-p)(Φ_{xx}-u_{0,xx})+p(Φ_{xx}+k^2Φ)=0 $ et $ Φ_{xx}+k^2Φ=0 $ car H est constant dans le premier cas

3) Développer l'expression obtenue pour différents ordres de p
Pour l'ordre 0 :
$ Φ_{0,xx}(x)-pΦ_{0,xx}(x)+pΦ_{0,xx}+pk^2Φ_0(x)=0 $
$ \LeftrightarrowΦ_{0,xx}(x)+pk^2Φ_0(x)=0 $ cette égalité est vraie pour tout p, donc en particulier pour p=0 donc :
$ Φ_{0,xx}(x)=0 $

En intégrant deux fois, on obtient :
$ \int_0^L Φ_{0,xx}(x)dx = Ax + B $, avec A et B deux constantes à déterminer
Or le sujet nous dit qu'à l'ordre 0, les conditions aux limites sont:
1) en x=0, $ Φ=1 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=A $
et $ Φx(x=L)=ikΦ(x=L)=ik(AL) $
donc $ A=ik(AL) $
D'où $ A=\frac{ik}{1-ikL} $;
Et on obtient $ Φ0(x)=Ax=\frac{ik}{1-ikL}*x $

Pour passer aux différents ordres, il suffira de réaliser une récurrence en faisant comme dans l'ordre 1 c'est-à-dire résoudre:
$ Φ1+k²∫∫Φ0+A2*x+B2=0 $ ( ce qui donne à l'ordre n : $ Φn+k²∫∫Φ(n-1)+A'*x+B'=0 $ )
On injecte dans l'équation ci-dessus l'expression de Φ0 trouvée précédemment.
On a alors: $ Φ1+k²([\frac{ik}{1-ikL}]\frac{x³}{3})+A2*x+B2=0 $
Or le sujet nous dit qu'à partir de l'ordre 1, les conditions aux limites sont:
1) en x=0, $ Φ=0 $ donne: $ B=0 $
2) en x=L, $ Φx=ikΦ $ donne $ Φx=-k²([\frac{ik}{1-ikL}]frac{L²}{2}]-A2 $
et $ Φx(x=L)=ikΦ(x=L)=-ik(-k²([ik/(1-ikL)]\frac{L³}{3})+A2*L) $
donc, par identification et en généralisant, on peut dire que $ A2=[\frac{ikΦxx - Φx}{1-ikL}]frac{L²}{2}] $

4) En utilisant la formule obtenue pour A, rentrer la récurrence déduite

Représentation pour le cas n°1

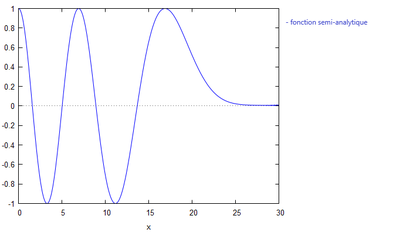
On obtient à l'aide de la méthode donnée ci-dessus codée sur Maxima, le graphique suivant:
Homotopie pour le cas avec p=20

Etude de la sensibilité du cas n°1

CAS n°2

Dans le deuxième cas, on s'intéresse une nouvelle fois à un domaine monodimensionnel plat de longueur L. On utilise la méthode standard utilisée pour le cas n°1, les calculs sont les mêmes et les résultats diffèrent en raison des conditions aux limites différentes du cas n°1 : la condition de flux aval est Φ_x=ik(2−Φ) et la réflexion totale en amont est Φ_x=0.

Solution analytique

$ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $

on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $

$ \Rightarrow\frac{∂^2Φ}{∂x^2}+k^2Φ=0 $ on obtient donc une équation différentielle homogène d'ordre 2 donc la solution est :

$ Φ=Ae^{-ikx}+Be^{ikx} $
On détermine A et B, deux constantes, grâce aux conditions limites :
en x = 0 : $ \frac{∂Φ(x)}{∂x}=ik(2-Φ) $

en x = L : $ \frac{∂Φ(x)}{∂x}=0 $

$ Φ(0)=1=A+B $ et $ \frac{∂Φ}{∂x}(0)=ik(2-Φ(0))=ik $

On trouve donc $ A=\frac{e^{ikL}}{2cos(kL)} $ et $ B=1-\frac{e^{ikL}}{2cos(kL)} $

Donc la solution analytique est $ \boxed{Φ=\frac{e^{ikL}}{2cos(kL)}e^{-ikx}+(1-\frac{e^{ikL}}{2cos(kL)})e^{ikx}} $


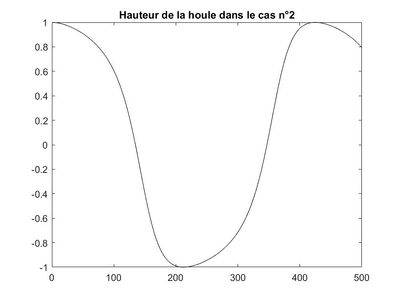
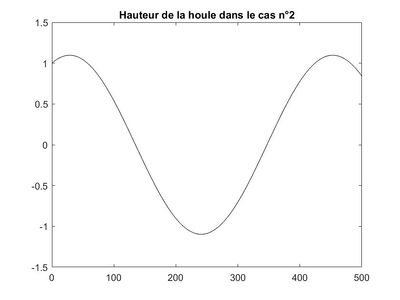
Nous avons tracé deux graphiques modélisant la hauteur de houle, celui de gauche correspond à $ H(x)=\mathbb{R}(Φ(x)/|Φ(x)|) $ et celui de droite à $ H(x)=\mathbb{R}(Φ(x)) $. On remarque que le résultat obtenu par homotopie est relativement proche de la courbe de gauche alors que celle de droite correspond bien à l'évolution de la hauteur de houle au cours du temps. Cela est logique puisqu'on utilise la première expression pour résoudre l'équation de Berkhoff de manière semi-analytique.

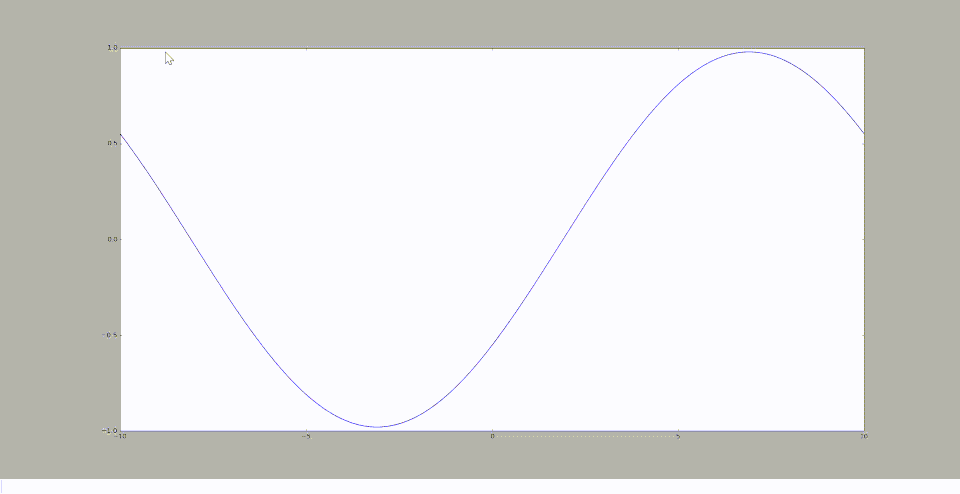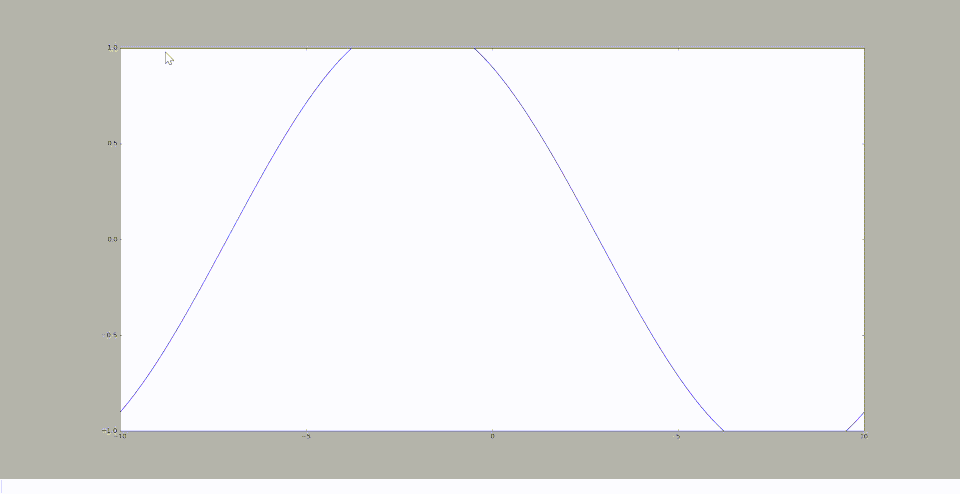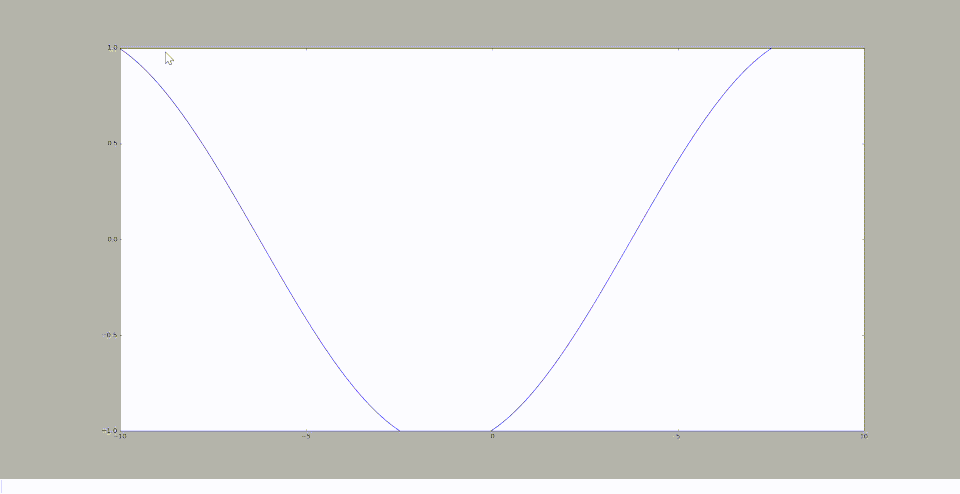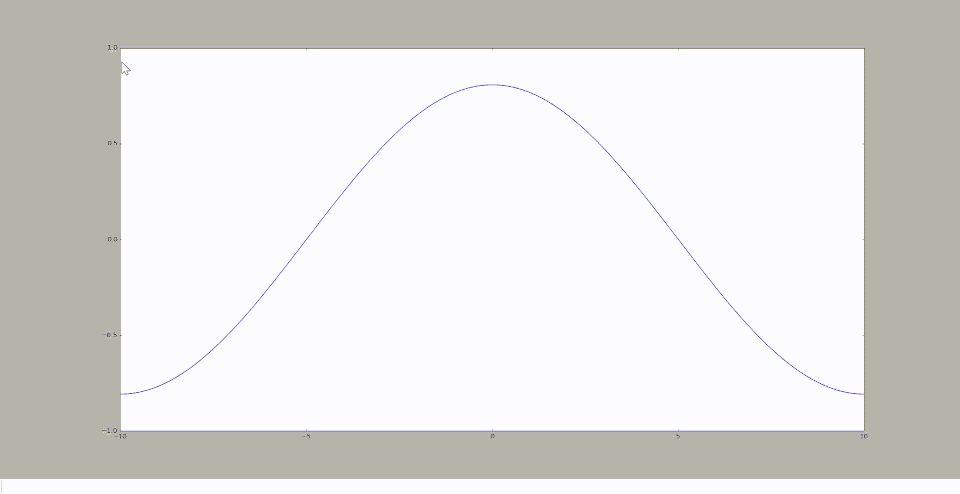
Homotopie

Représentation pour le cas n°2

Semblablement au cas n°1, on obtient l'équation suivante : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $
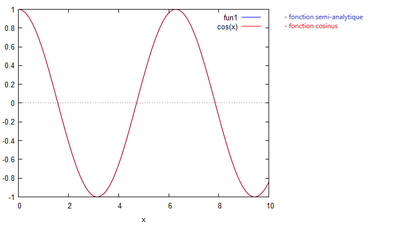
On obtient à l'aide de la méthode utilisée dans le cas n°1 (la méthode semi-analytique), le graphique suivant:

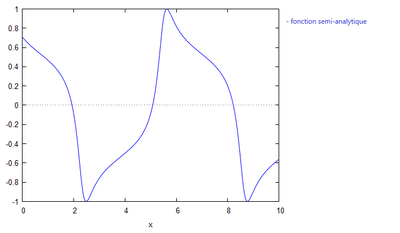
Etude de la sensibilité pour le cas n°2

Cas n°3

Dans le troisième cas, on s'intéresse à un domaine monodimensionnel de longueur L, avec cette fois une pente du fond constante avec entrée par l'aval d'une onde de fréquence unitaire. On considèrera que k=k0=cste

Solution analytique

On souhaite déterminer une solution analytique de l'équation de base transformée par changement de variable sous la forme d'une équation de type Bessel : $ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $, avec $ C=\surd gH $ et $ CC_g=gH $
Mais contrairement au cas 1 et 2, H n'est plus constante : $ H(x)=-sx+H_0 $, avec H_0 la hauteur initiale et s la pente du fond.

L'équation de Berkhoff devient alors $ H(x)\phi_{xx}(x)+H'(x)\phi_x(x)+k^2H(x)\phi(x)=0 $

On cherche à mettre cette équation sous forme d'équation de Bessel de type : $ x^2 \displaystyle\frac{\partial^2 ϕ}{\partial x^2} +x\frac{\partial ϕ}{\partial x} + x^2ϕ = 0 $
En prenant le changement de variable $ X=\dfrac{k}{s}(H_0-sx) $, on obtient : $ skX\dfrac{\partial^2\phi}{\partial X^2}+sk\dfrac{\partial\phi}{\partial X}+skX\phi=0 $

Une multiplication par X, et une division par sk permet alors d'obtenir une équation qui a la forme d'une équation de Bessel : $ X^2\phi_{XX}+X\phi_X+X^2\phi=0 $

La solution de cette équation est de la forme $ Φ(X) = A*J_0(X) + B*Y_0(X) $, avec $ J_0 $ la fonction de Bessel de première espèce et $ Y_0 $ la fonction de Bessel de seconde espèce.

D'après les conditions aux limites, avec $ Φ(X)=1 $ en aval et $ \frac{∂Φ}{∂x}=ikΦ(X) $ en amont , et sachant que $ X_0 = \frac{k}{s}H_0 $ et $ X_L = \frac{k}{s}(H_0 - sL) $, on obtient :

$ A=\frac{Y1(xL)−iY0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $ et $ B=\frac{J1(xL)+iJ0(xL)}{(Y1(xL)−iY0(xL))J0(x0)+(J1(xL)+iJ0(xL))Y0(x0)} $

Donc la solution analytique est: $ \boxed{Φ(x)=(A*J0(\dfrac{k}{s}(H_0-sx))+B*Y0(\dfrac{k}{s}(H_0-sx))} $

Homotopie

Particularité d cas n°3

Comme pour les précédents cas, on part de l'équation suivante : $ Φ=\sum_{k=0}^{\infty} p^kΦ_k $ et $ Φ_{xx}=\sum_{k=0}^{\infty} p^kΦ_{k,xx} $
Afin de prendre en compte la pente, caractérisé par un k=k0, on pose $ r = \frac{s}{H_0} $
On obtient alors: $ Φxx - pr*x*Φxx - pr*Φx + pk²(1-r*x)Φ = 0 $

Représentation pour le cas n°3

On obtient à l'aide de la méthode utilisée dans le cas n°1 (la méthode semi-analytique), le graphique suivant:

Etude de sensibilité pour le cas n°3

Cas n°6

Dans ce dernier cas on s'intéresse à un domaine bidimensionnel avec une bosse immergée parabolique sur le fond. On cherche à résoudre ce problème en coordonnées polaires puis en coordonnées cartésiennes.

Solution analytique

On part une nouvelle fois de l'équation de Berkhoff : $ ▽(CC_g▽Φ)+k^2CC_gΦ=0 $ avec $ C=\surd gH $ et $ CC_g=gH $

on a donc $ gH\frac{∂^2Φ}{∂x^2}+k^2gHΦ=0 $

La solution analytique correspondant à la déformation d'un train d'onde régulière autour d'une bosse est fournie par l'expression suivante :
$ Φ(r,θ)=Φ_0sum_{n=0}^{infty}j^{n+1}ε_n\frac{J_n(kr)H'_n^1(kR)-J_n'(kR)H_n^1(kR)}{H'_n^1(kR)}cos(nθ) $ (pb somme)

La hauteur de houle en tout point du domaine s'exprime de la manière suivante :
$ h(r,θ)=\mathbb{R}[Φ(r,θ)e^{jwt}] $

avec :
$ ε_n=2-δ_{n0} $
$ θ(r,θ) $: potentiel de houle
$ h(r,θ) $: hauteur de houle en coordonnées polaires repérée par rapport au centre de la bosse
$ h_0 $: hauteur de l'onde incidente
R : rayon de la bosse
T : période de l'onde
$ w=\frac{2π}{T} $
k : nombre d'onde
$ J_n $: fonctions de Bessel de 1ère espèce et d'ordre n
$ H_n^1 $: fonctions de Hankel de 1ère espèce et d'ordre n