Perte au ruissellement (HU)
Traduction anglaise : Runoff loss
Dernière mise à jour : 26/09/2023
mot en chantier
En hydrologie, les pertes au ruissellement (on dit également pertes à l’écoulement) correspondent à la partie de la lame d'eau reçue par un bassin versant qui ne contribue pas au ruissellement direct (c'est à dire qui s'infiltre ou qui s'évapotranspire).
Nota : Une partie des pertes au ruissellement peut cependant s'écouler à l'exutoire de façon décalée dans le temps (voir Ecoulement retardé (HU)).
Sommaire |
Différents types de pertes
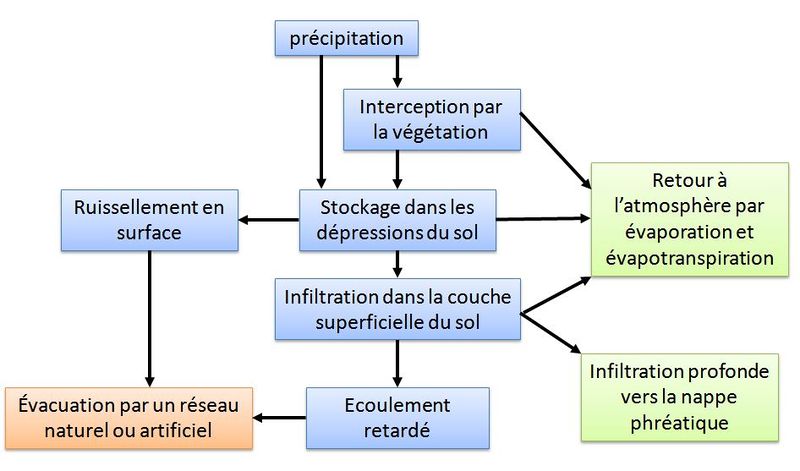
Les phénomènes susceptibles de provoquer des pertes au ruissellement sont l’évaporation, l'évapotranspiration, l’interception par la végétation, la rétention en surface et l’infiltration. Ils se produisent à différents moments et différents endroits sur le bassin versant (figure 1) .
Comportement des différents types de surface
Le comportement des surfaces des bassins versants vis à vis du ruissellement dépend d'un grand nombre de paramètres, parmi lesquels cinq sont prépondérants :
- le caractère plus ou moins artificialisé du sol : on sépare souvent, de façon d'ailleurs assez arbitraire, d'une part les sols recouverts de béton ou d'asphalte et supposés imperméables et, d'autre part, les autres sols, rarement totalement naturels, et supposés perméables ;
- la pente du sol, qui conditionne bien évidemment le partage entre la part qui ruisselle et celle qui s'infiltre ;
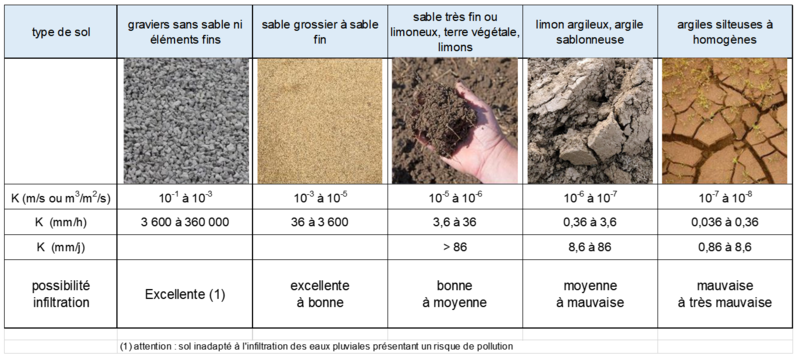
- la nature du substrat : la capacité d'infiltration peut varier de plus de 8 ordres de grandeur entre des sols très argileux et des sols très grossiers (figure 2) ; en pratique cette différence est souvent atténuée, du moins pour les pluies faibles et moyennes, par la présence en surface une couche de terre végétale plus ou moins épaisse ;
- le couvert végétal, qui joue un rôle au dessus du sol (interception par les feuilles) mais également à la surface du sol (présence de mousse, de litière de feuilles mortes, etc.) et dans le sol (rôle important des racines) ;
- la façon dont la surface est connectée au système de drainage : une rue équipée d'un réseau d'assainissement auquel elle est raccordée par un caniveau et des avaloirs n'aura pas le même comportement vis à vis du ruissellement qu'une route de campagne dont l'eau s'écoule vers les champs avoisinants.
Ces différentes caractéristiques peuvent varier de façon très importante pour des surfaces très proches et il est facile de comprendre que, sauf cas très particuliers, il est impossible de représenter en détail l'ensemble des phénomènes associés à ces différentes situations. La modélisation des pertes au ruissellement est donc toujours très globale, même dans le cas des modèles dits distribués.
Modélisation des pertes au ruissellement
Il existe de très nombreuses approches dont l'objet est le calcul des pertes au ruissellement, mais il faut noter que ce mot n'a pas toujours la même signification. Pour préciser les notions nous raisonnerons sur un bassin versant supposé homogène de surface $ A $.
Considérons les fonctions :
avec
- $ A $ : surface du bassin versant (m2) ;
- $ i(t) $ : intensité de pluie brute, supposée homogène sur $ A $ (m/s) ;
- $ Q_P(t) $ : débit précipité au temps t (m3/s) ;
- $ Q_S(t) $ : débit à l'exutoire du bassin versant (m3/s).
Coefficient de ruissellement et coefficient d'écoulement
On peut définir les pertes par un coefficient de ruissellement dont le but est de déterminer une caractéristique de l'hydrogramme, qui est, en général, le débit maximum (méthode rationnelle, méthode de Caquot, etc.). Par exemple :
ou
avec
- $ Q_Smax $ : valeur maximum de $ Q_S (t) $ ;
- $ Q_Pmax $ : valeur maximum de $ Q_P (t) $ ;
- $ t_P $ : durée de la pluie.
On peut également définir les pertes par une relation volumétrique entre le volume total ruisselé (écoulé à l'exutoire) et le volume total précipité :
On devrait alors plutôt parler de coefficient d'écoulement.
Schémas d'abattement
Il est également possible de faire varier les pertes au cours du temps. On introduit alors la notion de pluie nette. Le hyétogramme de pluie nette représente l'évolution dans le temps des intensités d'une pluie fictive, qui provoquerait le même hydrogramme de sortie sur un bassin versant de même surface que le bassin réel, mais ne présentant aucune perte. Le débit de pluie nette est égal à l'intensité de pluie nette multipliée par la surface du bassin versant ; il s'agit également d'une grandeur fictive :
avec
- $ inet(t) $ : intensité de pluie nette au temps t, supposée homogène sur $ A $ (m/s) ;
- $ Q_E(t) $ : débit de pluie nette au temps t (m3/s) ;
Si on conserve la notion de coefficient instantané de ruissellement, on peut écrire :
Dans ce cas on parle de fonction de production ou de schéma d'abattement, selon que l'on s'intéresse au débit produit ou à la lame d'eau "perdue".
Les schémas d'abattement sont en général fondés sur le principe de la séparation des pertes en une fraction initiale qui se produit avant que le ruissellement ne démarre, et une fraction continue qui se poursuit tout au long de l'événement. Les pertes initiales correspondent principalement au stockage dans les dépressions du sol, éventuellement à l'évapotranspiration (très faible durant la pluie) et à la rétention par la végétation. Les pertes continues représentent principalement l'infiltration.
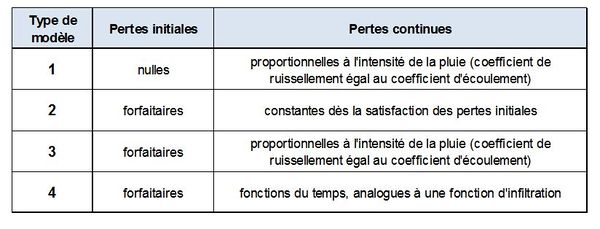
Les différents modèles peuvent, pour la plupart, se classer en quatre grandes familles, conformément au tableau de la figure 3, extrait de Desbordes (1974).
Aspects pratiques : modalités, contraintes et limites d'utilisation des modèles
Quelle que soit leur validité théorique et leur complexité, la qualité des différents modèles temporels de pertes ne peut être analysée qu'en liaison avec les modèles de transfert. Il n'existe en effet aucun procédé expérimental permettant de dissocier dans le temps ce qui s'écoule en surface et ce qui est perdu. Les seules grandeurs accessibles à la mesure sont l'intensité de pluie brute (ou le débit précipité) et le débit à l'exutoire.
Il n'est donc possible de vérifier que le rapport entre le volume total ruisselé et le volume total précipité ; la seule qualité objectivement vérifiable d'une modélisation des pertes est donc de bien représenter ce rapport.
L'aptitude à représenter la forme de l'hydrogramme à l'exutoire en fonction de la forme du hyétogramme précipité sur le bassin versant ne peut-être évaluée que si l'on prend en compte le couple modèle de pertes - modèle de ruissellement (ou fonction de production - fonction de transfert).
Par ailleurs l'importance relative des différentes pertes dépend bien évidemment de la nature du bassin versant, mais également de la pluie générant le ruissellement :
- une perte initiale de quelques mm sera négligeable pour une pluie apportant une centaine de mm mais sera déterminante pour une petite averse ;
- une perte continue de l'ordre du mm par heure (capacité d'infiltration moyenne d'une chaussée asphaltée du fait des fissurations), sera négligeable pour un orage d'été mais déterminante pour une pluie longue d'hiver.
On comprend donc facilement que le choix du modèle dépend de la nature du bassin versant mais également des objectifs de l'étude (Rammal et Berthier, 2020).
Pour les bassins versants urbains une perte initiale forfaitaire associée à un coefficient de ruissellement fonction des caractéristiques de la pluie constitue généralement le meilleur compromis (voir Coefficient de ruissellement (HU)). Un calage est généralement nécessaire pour bien évaluer les paramètres.
Pour les bassins versants naturels ou ruraux la prise en compte de l'évolution de la capacité d'infiltration des sols au cours du temps devient importante. Cette évolution peut être représentée par une saturation progressive des sols (modèles de type hortonien) comme le modèle de Horton ou le modèle de Green et Ampt. Elle peut également être représenté par une augmentation progressive de la surface contributive (voir Top Model (HU)).
Bibliographie :
- Desbordes, M. (1974) : Réflexions sur les méthodes de calcul des réseaux urbains d'assainissement ; thèse Docteur ingénieur ; Université des Sciences et Techniques du Languedoc ; Montpellier ; 171 p.
- Rammal, M., Berthier, E. (2020) : Amélioration des modélisations de la production du ruissellement des eaux pluviales urbaines lors des événements fréquents ; rapport Cerema pour l'OFB ; 62p. ; disponible sur www.cerema.fr
Voir aussi : Fonction de production et fonction de transfert (HU)
 S'abonner à un flux RSS
S'abonner à un flux RSS