Barré de Saint Venant (équations de) (HU)
Traduction anglaise : Barré de Saint-Venant's equations
Dernière mise à jour : 14/06/2024
Les équations de Barré de Saint Venant décrivent les écoulements à surface libre non permanents, unidimensionnels (1D) ou bidimensionnels (2D) (voir par exemple Mahmood & Yevjevich, 1975).
Leur résolution permet de définir, selon les coordonnées de l'écoulement, les variations temporelles du niveau d’eau (voir ligne d'eau) de la vitesse et du débit dans les sections retenues pour le calcul.
Sommaire |
Éléments d'historique
L'étude mathématique des écoulements à surface libre en régime transitoire n'est pas une discipline scientifique nouvelle. Elle a débuté, il y a déjà près de 250 ans, lors de l'essor de l'ensemble des théories mécaniques, avec les travaux de Laplace (1776) et de Lagrange (1781) sur la propagation d'ondes à la surface de canaux. Dès 1871, Barré de Saint Venant réussit à représenter mathématiquement le mouvement unidimensionnel des eaux à surface libre par un système d'équations aux dérivées partielles. Depuis lors, ces équations servent de base aux modèles mathématiques d'écoulement à surface libre. Les modèles mathématiques issus des équations de Barré de Saint Venant font partie de la famille des modèles mécanistes.
En raison de la grande quantité de calculs qu'elle nécessite, la résolution numérique des équations complètes de Saint-Venant n'est possible que depuis l'invention des ordinateurs, c'est à dire la deuxième moitié du 20ème siècle.
Écriture des équations de Barré de Saint venant
Hypothèses générales
Ces équations ont tout d'abord été établies pour des écoulements unidimensionnels. Ceci suppose donc :
- que l'écoulement se fasse le long d'une direction privilégiée $ x $ ;
- que les caractéristiques de ces écoulements (en particulier leur vitesse) puissent être considérées comme correctement approchées par leurs valeurs moyennes dans une section droite orthogonale à $ x $.
Les variables sont le débit $ Q(x,t) $ et la section mouillée $ S(x,t) $, ou la vitesse $ V(x,t) $ et le tirant d'eau $ h(x,t) $, ou encore la cote $ z(x,t) $ de la surface libre, toutes fonctions des seuls paramètres abscisse x, temps t. Pour simplifier l'écriture ces variables seront simplement notées $ Q{,} S{,} V{,} h{,} z $.
La vitesse considérée ici est donc une vitesse moyenne débitante, telle que l'on puisse écrire : $ Q = V.S $, et la hauteur transversale est supposée constante sur la largeur de la surface libre. Il n'est donc pas possible de tenir compte de surélévation intrados-extrados dans les coudes, ce qui exclut, en toute rigueur, de simuler les écoulements dans des tronçons présentant des courbures importantes.
Une hypothèse importante sous-jacente à l'unidimensionnalité réside dans la répartition hydrostatique des pressions, hypothèse qui permet d'écrire la résultante des forces de pression sous la forme :
Ceci suppose qu'il n'y a pas de composante verticale de la vitesse et donc qu'il n'y a pas de surélévation brutale de la ligne d'eau ou des fonds.
Remarque : malgré ces limites théoriques, il arrive cependant souvent que ces équations soient utilisées en dehors de leur champ normal d'application, par exemple pour traiter de la propagation d'ondes associées à des manœuvres brusques, telles que des lâchures de barrage, des ouvertures rapides de vannes, etc. Une forme particulière d'écriture de ces équations (formulation dite conservative) associée à un mode spécifique de résolution numérique (schémas à capture de chocs) permet cependant de représenter les fronts d'onde raides et est également compatible avec la représentation des ressauts hydrauliques (voir § "Écriture conservative").
Les équations de Barré de Saint Venant sont formées d'un couple de deux équations aux dérivées partielles en $ x $ et $ t $, traduisant :
- la conservation de la masse ;
- la loi fondamentale de la dynamique.
Pour les réseaux d'assainissement, les couples de variables les plus couramment utilisées pour écrire ces équations sont $ (Q, h) $ ou $ (V, h) $. Dans le cas des milieux naturels où les pentes sont difficiles à définir on utilise plutôt $ (Q, z) $ ou $ (V, z) $.
Conservation de la masse
L'équation dite de continuité traduit la conservation de la masse et s'écrit :
où $ q $ représente un éventuel débit latéral, par unité de longueur, positif ou négatif selon qu'il s'agit respectivement d'un débit d'apport ou de fuite.
En notant $ B(h) $ la largeur de la surface libre, on peut écrire :
L'équation (2) devient alors, avec le couple de variables ($ Q, h $) :
La même équation peut également s'écrire avec le couple de variables ($ V,h $) en utilisant la relation : $ Q = V.S $.
Conservation de la quantité de mouvement
La seconde équation aux dérivées partielles est l'équation dynamique qui traduit la conservation de la quantité de mouvement, ou encore la loi fondamentale de la mécanique.
L'une des formulations les plus classiques est la suivante :
Avec :
- $ I $ : pente du canal (m/m) ;
- $ J $ : pente de la ligne d'énergie ou pertes de charge par unité de longueur (m/m) ;
- $ k $ : coefficient compris entre -1 et +1 ; avec
- $ k $ positif si le débit latéral est entrant (apport de quantité de mouvement) et négatif s'il est sortant (export de quantité de mouvement) ;
- $ k $ proche de 0 si le débit d'apport (ou de fuite) est approximativement orthogonal à $ x $, de façon à ne pas apporter (ou emporter) en même temps une quantité de mouvement, tandis $ k=1 $ suppose que le débit d'apport (ou de fuite) apporte (emporte) avec lui sa quantité de mouvement avec une vitesse égale à celle de l'écoulement principal.
Nota : En pratique, dans les réseaux d'assainissement, on néglige généralement la quantité de mouvement apportée ou emportée par les apports ou les fuites latérales de débit.
L'emploi de la pente $ I $ dans l'expression des forces de pesanteur sous-entend des pentes faibles. Enfin, le fluide est supposé incompressible.
Avec ces différentes hypothèses et en divisant par S pour faire intervenir la vitesse moyenne de l'écoulement, l'équation (5) peut finalement se mettre sous la forme classique :
Écriture compacte
Il est également possible d'utiliser une écriture vectorielle compacte des équations. En posant :
on peut alors écrire :
Nota : Il existe encore d'autres formes pour ce système d'équations ; en particulier, pour représenter les écoulements naturels, on préfère généralement travailler en cote $ z $ de la surface libre ; les équations sont identiques à la condition de remplacer $ h $ par $ z $ et de prendre $ I = 0 $.
Écriture conservative
Il est également possible de compléter la relation (5), pour obtenir une formulation dite conservative permettant de prendre en compte les ressauts hydrauliques et les fronts d’onde (Toro, 2009). A une dimension, cette formulation est alors constituée des deux équations suivantes :
en posant :
Avec :
- $ B $ : largeur miroir (m).
Pour prendre en compte les ressauts hydrauliques et les fronts d'onde, il est nécessaire de résoudre ce système d'équations en utilisant un schéma numérique à capture de choc (Toro, 2009).
Estimation des pertes de charge
Il est nécessaire de faire l'hypothèse que les pertes de charges pour les écoulements non permanents peuvent s'exprimer de la même façon que pour les écoulements permanents graduellement variés (Voir Pertes de charge), c'est à dire d'écrire $ J $ sous la forme :
Avec :
- $ λ $ : coefficient de pertes de charge (sans dimension) ;
- $ D_h $ : diamètre hydraulique de la conduite ($ D_h = 4.R_h $) (m) ;
- $ R_h $ : rayon hydraulique de la conduite (m).
Le coefficient de pertes de charge est fonction de la rugosité des parois, de la viscosité du fluide, du diamètre hydraulique de la conduite, mais également des « macro-aspérités » du réseau (branchements, câbles, échelles, arrivées latérales de débit, etc.). Il existe de nombreuses formules pour le calculer.
Les plus utilisées sont celles de Manning-Strickler, de Colebrook et dans une moindre mesure de Bazin.
Fermeture des équations
Les équations de Barré de Saint Venant sont valables sur un bief régulier et pour un temps courant. Pour les résoudre, il est nécessaire de "fermer" le système d'équations en rajoutant des conditions aux limites aux extrémités du bief. Une condition initiale cohérente précisant la valeur des grandeurs choisies au début du calcul est également indispensable.
Le problème posé par le choix des conditions aux limites est le plus difficile à résoudre. En effet, selon que l'écoulement est de type fluvial ou torrentiel les conditions à imposer sont de nature différente :
- dans le cas d'un écoulement fluvial, les conditions hydrauliques dépendent à la fois de l'amont et de l'aval, il faut donc des conditions à la limite amont et à la limite aval ;
- dans le cas d'un écoulement torrentiel, les conditions hydrauliques ne dépendent que de l'amont et les conditions aux limites doivent être définies à l'amont.
La nature de l'écoulement (fluvial ou torrentiel) peut varier d'un bief à un autre, pour un même bief d'un instant à un autre et même à l'intérieur d'un même bief. Or on ne connait la nature de l'écoulement en un point qu'une fois la résolution terminée. En théorie seule une résolution itérative permet donc de résoudre cette difficulté. Pour lever cette difficulté la plupart des logiciels commerciaux simplifient les équations lorsque l'écoulement risque de devenir torrentiel de façon à ne plus avoir besoin que d'une condition à la limite amont.
Résolution des équations de Barré de Saint Venant
Plusieurs méthodes peuvent être envisagées pour résoudre les équations de Barré de Saint-Venant. Les plus classiques utilisent des schémas de différences finies. Des schémas mixtes combinant différences finies, éléments ou volumes finis, sont également possibles. La résolution est le plus souvent directe, mais peut également faire appel à la théorie des caractéristiques qui permet de remplacer le système d'équations aux dérivées partielles par une équation différentielle. Les équations peuvent éventuellement être simplifiées avant leur résolution.
Simplifications possibles
La résolution directe des équations complètes de Barré de Saint Venant n'est possible que depuis l'apparition, à la fin des années 1960, d'ordinateurs suffisamment puissants pour permettre le développement des logiciels de résolution. C'est pourquoi, avant cette période, on a cherché à le simplifier. Les approches de ce type présentent d'ailleurs toujours de l'intérêt pour les logiciels techniques car elles permettent de construire des schémas plus robustes et plus rapides, tout en fournissant des réponses suffisamment précises pour certains cas d'application. Les simplifications utilisées reposent sur les considérations suivantes :
- les ordres de grandeur relatifs des différents termes des équations de Barre de Saint-Venant dépendent des caractéristiques géométriques et des conditions aux limites ;
- l'équation de continuité ne contient que deux termes ; en régime non-permanent, aucune des deux dérivées partielles du premier membre ne peut être nulle ou négligeable ; cette équation ne peut donc pas être simplifiée ;
- l'équation de conservation de la quantité de mouvement (équation dynamique) contient cinq (ou six s'il y a débit d'apport) termes et un assez grand nombre de simplifications sont possibles. En effet, il est rare que les cinq termes de cette équation soient tous du même ordre de grandeur.
Par exemple, la signification des termes dans l'équation (6) est la suivante :
- le terme d'inertie $ \displaystyle\frac{\partial V}{\partial t} $ dépend essentiellement du temps, donc de la vitesse de montée de la crue ;
- le terme d'accélération convective $ V.\displaystyle\frac{\partial V}{\partial x} $ dépend plutôt de la géométrie des canalisations ;
- le terme $ \displaystyle{g.\frac{\partial h}{\partial x}} $ dépend de la pente de la ligne d'eau ;
- le terme $ g.(I-J) $ dépend de la pente et des frottements.
La simplification la plus courante consiste à considérer les termes d'inertie et d'accélération convective comme négligeables. On obtient alors le modèle de l'onde de crue diffusante :
Même s'ils donnent des résultats souvent acceptables dans de nombreux cas, ces modèles simplifiés ont perdu beaucoup d'intérêt avec le développement de logiciels commerciaux performants capables de résoudre rapidement les équations complètes même sur des réseaux complexes.
Résolution numérique des équations de Barré de Saint Venant
Les méthodes numériques de résolution habituellement utilisées sont des schémas implicites ou explicites de différences finies (plus rarement d'éléments finis) s'appliquant aux équations originelles.
Les schémas explicites de différences finies sont les plus simples. Cependant, il est nécessaire de prendre un pas de temps très court, du fait de la condition de stabilité numérique (condition de Courant-Friedrisch-Lewy) qui impose :
De ce fait, les méthodes numériques habituellement utilisées pour résoudre les équations de Saint-Venant utilisent plutôt des schémas implicites. Ces schémas permettent en effet des variations importantes des caractéristiques de l'écoulement. Ils ont des conditions de stabilité numérique (contraintes sur le pas de temps et le pas d'espace) moins sévères que les schémas explicites.
Ces schémas implicites ont cependant l'inconvénient d'imposer la résolution à chaque pas de temps d'un système d'équations qui doivent être linéarisées pour être résolues. Le nombre d'équations étant égal au double du nombre de points de calcul, il peut dépasser plusieurs dizaines de milliers si le réseau étudié est étendu. La résolution pas de temps par pas de temps exige donc un temps de calcul important qui, même avec les ordinateurs actuels, peut être pénalisant si l'on souhaite simuler des durées importantes (séries chronologiques de pluies par exemple).
Difficultés spécifiques à la résolution dans le cas des réseaux d'assainissement
En assainissement, l'application des équations de Barré de Saint Venant nécessite quelques adaptations et approximations en raison du contexte très particulier d'application :
- collecteurs fermés et passage des écoulements à surface libre à des écoulements en charge ;
- présence d'ouvrages spéciaux et de singularités multiples.
Traitement des écoulements en charge
Du point de vue de la mécanique, les écoulements en charge semblent plus simples à représenter que les écoulements à surface libre. La section mouillée est alors égale à la section du collecteur et la propagation de l'onde est quasi instantanée. C'est donc moins le phénomène lui-même que la partie du réseau qui se met en charge qu'il est difficile de modéliser. En effet, les mises en charge évoluent au cours du temps et se déplacent à l'intérieur du réseau. Il est donc indispensable que le modèle de simulation des écoulements en charge soit compatible avec le modèle de simulation des écoulements à surface libre, les deux types de modèle devant s'appliquer alternativement aux mêmes parties du réseau. Cette contrainte rend particulièrement délicate la représentation des mises en charge dans les modèles de simulation des écoulements en réseau d'assainissement, et conduit le plus souvent à des approximations importantes. La plus grande difficulté réside dans la détermination des zones mises en charge à chaque instant. En effet, la hauteur de charge dans une canalisation est fonction des débits amont qui y parviennent, mais réciproquement, ces débits sont influencés par la hauteur de charge. C'est pourquoi la plupart des méthodes construites à ce jour pour simuler les mises en charge utilisent des artifices de calcul.
L'artifice de calcul le plus couramment utilisé est celui de la fente de Preismann (Abbott & Cunge, 1982). Cette méthode consiste à considérer la canalisation ouverte sur sa partie supérieure et reliée à l'air libre par une fente très fine comme l'illustre la figure 1. Le calcul peut être ainsi mené entièrement à surface libre, la hauteur d'eau dans la fente ($ h $) représentant fictivement la hauteur de mise en charge.
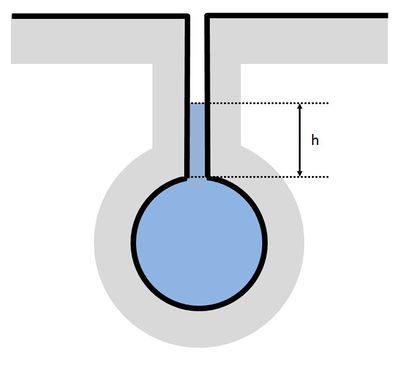
La méthode a l'avantage de délimiter une zone de mise en charge et de quantifier cette charge. Cependant, elle ne représente pas correctement l'influence de cette mise en charge sur l'écoulement amont, car elle néglige les phénomènes d'onde dynamique qui s'ensuivent (voir Mise en charge (HU)). La zone de mise en charge et l'écoulement à surface libre la précédant ne sont donc pas exactement simulés. En revanche, cette méthode permet de simuler des phénomènes de mise en charge provenant d'une forte influence aval même si le débit transitant dans le tronçon est inférieur au débit capable. Elle peut également être utilisée pour représenter les stockages supplémentaires susceptibles de se produire dans les parties non représentées du réseau (conduites tertiaires, branchements, cheminées, etc.) en jouant sur l'épaisseur de la fente.
Singularités hydrauliques
Les réseaux contiennent un très un grand nombre d'ouvrages ou de singularités : extrémité amont, chute, seuil, jonction ou défluence, changement de forme de section ou de pente, ouvrage spécial (station de pompage, bassin de retenue, déversoir d'orage, etc.) ou exutoire, qui peut lui-même être de différents types.
Ces singularités doivent être modélisées à l'aide de modèles indépendants, compatibles avec le modèle de Barré de Saint Venant. Ces modèles spécifiques doivent utiliser les mêmes grandeurs que le modèle de base, c'est-à-dire les couples hauteur-vitesse ou les couples hauteur-débit.
La plupart des logiciels considèrent ces singularités comme ponctuelles. Elles constituent alors un point de calcul sur lesquels on écrit une relation spécifique décrivant son fonctionnement. On trouvera aux articles traitant de ces différents éléments des pistes pour écrire ces équations.
La deuxième équation est le plus souvent en écrivant que les hauteurs d'eau dans le nœud représentant la singularité est la même que dans les extrémités des tronçons de calcul qui lui sont raccordés. Certains auteurs recommandent de remplacer l'égalité des hauteurs par l'égalité des charges ou par la conservation des quantités de mouvement (Frerot, 1987). Ces hypothèses sont cependant plus difficiles à utiliser
Dans tous les cas, les modèles utilisés sur les singularités sont plus ou moins empiriques, souvent très éloignés de la rigueur mécanicienne prêtée aux équations de Barré de Saint-Venant. Ce sont donc ces modèles qui, dans la plupart des cas, limitent les performances des modèles de simulation hydraulique des réseaux.
Cas des équations à deux dimensions
Il est également possible d'écrire les équations de Barré de Saint Venant en considérant deux dimensions d'espace ($ x $ et $ y $) et donc de décomposer le vecteur vitesse en deux composantes (Cunge et al., 1980). L'équation (10) devient alors :
Ce type de représentation est peu utile pour les réseaux d'assainissement pour lesquels une représentation filaire est suffisante. Elle peut être intéressante pour simuler les crues de rivière (en particulier pour représenter les écoulements dans le lit majeur). Sur le plan théorique le calcul n'est pas plus compliqué. En revanche la nécessité de mailler l'espace de travail a deux dimensions peut conduire à un très grand nombre de nœuds de calcul et donc à des temps de résolution importants (voir Modèle d'écoulement en réseau et en cours d'eau (HU), Débordement (HU)).
Bibliographie :
- Abbott, M.B., Cunge, J.A. eds. (1982) : Engineering applications of computational hydraulics: homage to Alexandre Preissmann ; Pitman, Boston.
- Cunge, J.A., Holly, F.M., Verwey, A. (1980) : Practical aspects of computational river hydraulics ; Pitman Pub. ; London.
- Frerot, A. (1987) : Procédures d'optimisation des consignes de gestion d'un réseau d'assainissement automatisé ; thèse de doctorat ; ENPC - Paris ; 296p. + annexes7.
- Mahmood, K. , Yevjevich, V. (1975) : Unsteady flow in open channels ; (3 volumes) ; Water Ressources Publications ; Fort Collins ; Colorado.
- Toro, E.F. (2009) : Riemann Solvers and Numerical Methods for Fluid Dynamics ; Springer eBooks ; disponible sur https://doi.org/10.1007/b79761
 S'abonner à un flux RSS
S'abonner à un flux RSS